Mravenec na tyči
Úloha číslo: 120
Tenká tyč OA délky R se otáčí úhlovou rychlostí ω ve směru pohybu hodinových ručiček kolem osy, která je kolmá k tyči a prochází bodem O. Po tyči od bodu O leze ve směru k bodu A mravenec konstantní rychlostí \(\vec{v}\) vzhledem k tyči. Popište průběh polohy mravence v laboratorní vztažné soustavě, byl-li v čase t = 0 s právě ve středu tyče.
Nápověda 1: Obrázek situace
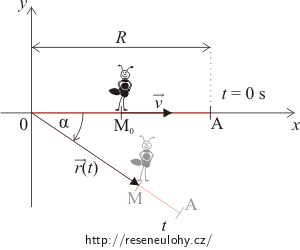
Počátek souřadné soustavy zvolte v bodě 0 (bod O) a počáteční polohu tyče tak, že splývá s osou x. Nakreslete situaci pro čas t = 0 s a vyznačte polohu mravence. Pak nakreslete, jak se pootočí tyč za okamžik t a kam popoleze mravenec. Vyznačte polohový vektor mravence v čase t.
Nápověda 2: Polohový vektor mravence
O jaký kus popolezl mravenec za čas t a jak dlouhý bude polohový vektor mravence v čase t? O jaký úhel se pootočila tyč za čas t?
Pomocí úhlu α vyjádřete x-ovou a y-ovou složku polohového vektoru \(\vec{r}\left(t\right)\).
CELKOVÉ ŘEŠENÍ
Obrázek situace:
Pohyb rozložíme na pohyb rovnoměrný přímočarý s rychlostí o velikosti v a na pohyb po kružnici s úhlovou rychlostí o velikosti ω.
Za čas t mravenec popoleze o vzdálenost vt.
Délka polohového vektoru v čase t bude:
\[r\left(t\right)\,=\,vt+\frac{R}{2}.\tag{1}\]Tyč se pootočí o úhel:
\[\alpha\,=\,\omega{t}.\]Délka polohového vektoru se tedy mění s časem podle vztahu (1):
\[r\left(t\right)\,=\,vt+\frac{R}{2}.\]Průmět polohového vektoru do osy x je roven
\[x\left(t\right)\,=\,r\left(t\right)\cos\alpha\,=\,\left(vt+\frac{R}{2}\right)\cos\omega{t}.\]Průmět polohového vektoru do osy y je roven
\[y\left(t\right)\,=\,-r\left(t\right)\sin\alpha\,=\,-\left(vt+\frac{R}{2}\right)\sin\omega{t}.\](Průmět jde do záporného směru osy y, proto \(-\).)
Polohový vektor pak vyjádříme jako vektorový součet jeho složek:
\[\vec{r}\left(t\right)\,=\, x\left(t\right)\vec{i} + y\left(t\right)\vec{j},\]kde \(\vec{i}\), \(\vec{j},\) jsou jednotkové vektory ve směru os x a y.
Po dosazení dostáváme:
\[\vec{r}\left(t\right)\,=\, \left(vt+\frac{R}{2}\right)\cos\omega{t} \vec{i}-\left(vt+\frac{R}{2}\right)\sin\omega{t } \vec{j}.\]Odpověď
Polohový vektor mravence se s časem mění podle vztahu:
\[\vec{r}\left(t\right)\,=\, \left(vt+\frac{R}{2}\right)\cos\omega{t} \vec{i}-\left(vt+\frac{R}{2}\right)\sin\omega{t } \vec{j},\]kde \(\vec{i}\), \(\vec{j}\) jsou jednotkové vektory ve směru os x a y.
Vizualizace pohybu
Následující aplet slouží k vizualizaci pohybu mravence na tyči. Polohu mravence v daném čase určuje námi nalezený polohový vektor \(\vec{r}_{(t)}\), který je níže znázorněn modře. Kliknutím na tlačítko „Zapnout animaci“ se spustí animace pohybu, opětovným kliknutím se animace zastaví. Čas \(t\) je možné měnit na posuvníku. Kliknutím na tlačítko „Zobrazit stopu mravence“ se zapne, nebo vypne stopa bodu M. Obdobně tlačítko „Zobrazit trajektorii mravence“ vykreslí trajektorii bodu M. Tlačítko „Reset“ vrátí aplet do původního stavu.
Jak je z apletu dobře vidět, trajektorií tohoto mravence je spirála.