Einstein na plošině
Úloha číslo: 1263
Vodorovná hmotná plošina se otáčí kolem svislé osy a koná \(n_1\) otáček za sekundu. Ve středu plošiny stojí člověk, který drží v rozpažených rukou dvě stejná závaží, každé o hmotnosti \(m\). Vzdálenost závaží je přitom \(2l_1\). Potom člověk skrčí paže tak, že se vzdálenost závaží zmenší na \(2l_2\). Soustava tvořená plošinou, člověkem a závažími pak koná \(n_2\) otáček za sekundu.
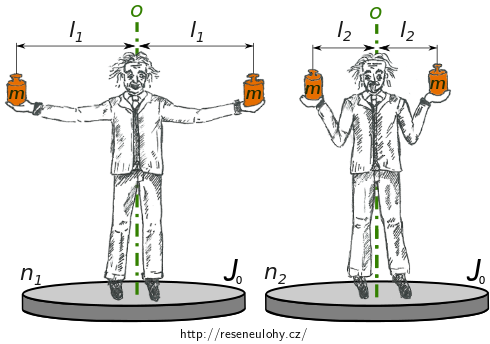
- Určete moment setrvačnosti plošiny.
- Určete práci, kterou člověk vykoná tím, že závaží přitáhne k tělu.
Hmotnost člověka stojícího ve středu plošiny včetně jeho paží zanedbejte.
Průpravná rukojeť
Moment setrvačnostiNachází-li se hmotný bod s hmotností \(m\) ve vzdálenosti \(r\) od osy otáčení, je jeho moment setrvačnosti vůči této ose
\[J = mr^2.\]Moment setrvačnosti je aditivní veličina. Jsou-li \(r_i\) vzdálenosti hmotných bodů od osy otáčení a \(m_i\) jejich hmotnosti, je moment setrvačnosti soustavy těchto bodů vůči udané ose
\[J = \sum_{i=1}^{n} J_i = \sum_{i=1}^{n} m_i r_i^2.\tag{1}\] Moment hybnostiDruhá věta impulsová říká, že časová změna momentu hybnosti soustavy je rovna výslednici momentů vnějších sil působících na soustavu, tj.
\[\frac{\mathrm{d}\vec{L}}{\mathrm{d}t} = \sum_{i=1}^{n} \vec{M_i ^\mathrm{ex}}.\]Je-li výslednice momentů vnějších sil nulová, tj. \(\sum_{i=1}^n \vec{M_i ^\mathrm{ex}} = \vec{0}\), pak
\[\frac{\mathrm{d}\vec{L}}{\mathrm{d}t} = 0 \quad \Longrightarrow \quad \vec{L} = \overset{\longrightarrow}{konst.}\tag{2}\]Tento výsledek není ničím jiným než zákonem zachování momentu hybnosti.
Je-li výslednice momentů vnějších sil působících na soustavu nulová, je její moment hybnosti konstantní.Rotuje-li soustava kolem osy \(o\) úhlovou rychlostí \({\omega}\) a je-li moment setrvačnosti vzhledem k rotační ose \(J\), je její moment hybnosti dán vztahem
\[L_\mathrm{o} = J \omega. \tag{3}\] Energie rotačního pohybuKinetická energie rotačního pohybu soustavy, která rotuje úhlovou rychlostí \(\omega\) kolem osy, vůči níž má soustava moment setrvačnosti \(J\), je
\[E_\mathrm{k} = \frac12 J \omega^2.\tag{4}\]Zápis
\(n_1 \) počet otáček za \(1~\mathrm{s}\) (frekvence otáčení) při rozpažení \(n_2 \) počet otáček za \(1~\mathrm{s}\) (frekvence otáčení) po skrčení rukou \(l_1\) vzdálenost závaží od osy otáčení při rozpažení \(l_2\) vzdálenost závaží od osy otáčení po skrčení rukou \(m\) hmotnost jednoho závaží
\(J = \mathrm{?} \) moment setrvačnosti plošiny \(W = \mathrm{?} \) člověkem vykonaná práce při přitažení rukou k tělu Nápověda 1 – zákon zachování momentu hybnosti
Předpokládáme, že plošina se otáčí bez tření, její pohyb není ničím bržděn.Jaké vnější síly na soustavu působí? Jaký je jejich celkový výsledný moment?
Jsou pro otáčející se soustavu splněny předpoklady zákona zachování momentu hybnosti? Pokuste se jej sestavit.
Nápověda 2 – vykonaná práce
Na závaží v rotující soustavě působí odstředivá síla. Aby závaží Einsteinovi neuletěla, musí působit silou proti ní. Při přitažení rukou k tělu tedy působil silou po určité dráze a vykonal práci.
Jak se projeví práce dodaná člověkem v soustavě?
CELKOVÉ ŘEŠENÍ
Momenty tíhových sil jsou vzhledem k ose otáčení nulové. Zanedbáváme-li momenty třecí síly v ložisku plošiny a tření o vzduch, je celkový moment vnějších sil nulový. Předpoklad zákona zachování momentu hybnosti (2) je splněn.
Dle zákona zachování momentu hybnosti je celkový moment hybnosti soustavy při rozpažených rukou \(\vec{L}_\mathrm{1}\) roven celkovému momentu hybnosti soustavy při rukou skrčených \(\vec{L}_\mathrm{2}\), tj.
\[\vec{L}_\mathrm{1} = \vec{L}_\mathrm{2}.\] Vzhledem k tomu, že soustava rotuje kolem stálé osy, je vektor momentu hybnosti konstantní a s ním i jeho velikost, tedy \[ L_1 = L_2. \] Užitím vztahu (3) a vyjádřením úhlových rychlostí pomocí frekvencí otáčení \(n_1\), \(n_2\) získáme \[ J_1 \omega_1 = J_2 \omega_2, \] \[ J_1 2\pi n_1 = J_2 2\pi n_2. \tag{5}\]Momenty setrvačnosti soustavy vůči ose rotace při rukou rozpažených (\(J_1\)) a skrčených (\(J_2\)) jsou dle (1)
\[J_1 = J_0 + 2ml_1^2,\tag{6}\] \[J_2 = J_0 + 2ml_2^2,\tag{7}\]kde \(J_0\) je moment setrvačnosti plošiny a součin \(2ml_i^2\) představuje moment setrvačnosti obou závaží, která jsme pro jednoduchost nahradili hmotnými body.
Dosazením (6) a (7) do (5) získáme zákon zachování momentu hybnosti ve tvaru
\[\left( J_0 + 2ml_1^2\right)2\pi n_1 = \left( J_0 + 2ml_2^2\right)2\pi n_2,\] odtud jednoduchými úpravami získáme hledaný moment setrvačnosti \(J_0:\) \[J_0 = 2m\frac{l_1^2 n_1 - l_2^2 n_2}{n_2 - n_1}.\tag{8}\]
Člověkem vykonáná práce se projeví vzrůstem kinetické energie soustavy, tj.
\[ E_\mathrm{k_2} = E_\mathrm{k_1} + W \qquad \Rightarrow \qquad W = E_\mathrm{k_2} - E_\mathrm{k_1},\tag{9}\]kde \(E_\mathrm{k_1}\) a \(E_\mathrm{k_2}\) jsou kinetické energie soustavy při natažených a skrčených rukou.
Vyjádříme kinetické energie rotačního pohybu (4) v obou situacích. Za momenty setrvačnosti dosadíme ze vztahů (6) a (7), úhlovou rychlost opět vyjádříme pomocí zadaných frekvencí otáčení:
\[E_{\mathrm{k}1} = \frac{1}{2}J_1 \omega_1^2 = 2\pi^2 (J_0 + 2ml_1^2){n_1}^2, \tag{10}\] \[E_{\mathrm{k}2} = \frac{1}{2}J_2 \omega_2^2 = 2\pi^2 (J_0 + 2ml_2^2){n_2}^2. \tag{11}\]Dosazením vztahů (10) a (11) do vztahu vyjádření vykonané práce (9) získáme
\[W = E_\mathrm{k_2} - E_\mathrm{k_1} = 2\pi^2\left[ (J_0 + 2ml_2^2) n_2^2 - (J_0 + 2ml_1^2)n_1^2\right] = \] \[ = 2\pi^2\left[ J_0 (n_2^2 - n_1^2) + 2m(l_2^2 n_2^2 - l_1^2 n_1^2)\right]. \]Dosazením za moment setrvačnosti \(J_0\) z rovnice (8) získáme výsledný vztah:
\[ W = 2\pi^2\left[ J_0 (n_2^2 - n_1^2) + 2m(l_2^2 n_2^2 - l_1^2 n_1^2)\right] = \] \[ = 2\pi^2\left[2m\frac{l_1^2 n_1 - l_2^2 n_2}{n_2 - n_1} (n_2^2 - n_1^2) + 2m(l_2^2 n_2^2 - l_1^2 n_1^2)\right]= \] \[ = 4\pi^2 m \left[(l_1^2 n_1 - l_2^2 n_2)(n_2 + n_1) + l_2^2 n_2^2 - l_1^2 n_1^2\right]= \] \[ =4\pi^2 m (l_1^2 - l_2^2) n_1 n_2. \]Odpověď
- Moment setrvačnosti plošiny je \[J_0 = 2m\frac{l_1^2 n_1 - l_2^2 n_2}{n_2 - n_1}.\]
- Práce vykonaná člověkem při skrčení paží je \[W = 4\pi^2 m \left(l_1^2 - l_2^2\right) n_1 n_2 .\]



