Kolébání půlválce
Úloha číslo: 537
Homogenní půlválec o poloměru r a hmotnosti m leží na vodorovné rovině.
a) Určete moment setrvačnosti půlválce vzhledem k přímce, ve které se půlválec dotýká roviny.
b) Půlválec vykloníme o malý úhel z rovnovážné polohy a pustíme. S jakou periodou se bude kolébat?
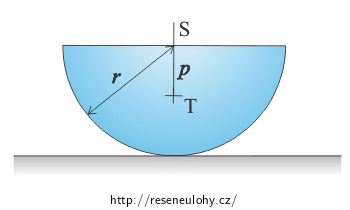
Předpokládáme, že tření mezi půlválcem a rovinou je dostatečně velké, aby nedošlo k prokluzování, a že valivý odpor je zanedbatelný.
Těžiště půlválce se nachází ve vzdálenosti \(p=\frac{4r}{3\pi}\) od bodu S.
Pro malé úhly můžete použít aproximace (přibližného vztahu) \(\sin\alpha\dot{=}\alpha\,,\) \(\cos\alpha=1-2sin^2\frac{\alpha}{2}\dot{=}1-\frac{\alpha^2}{2}\,.\)
Nápověda a) 1
K výpočtu momentu setrvačnosti využijte Steinerovu větu a znalost momentu setrvačnosti celého válce vzhledem k ose procházející středy podstav.
Nápověda b) 1
Předpokládejme, že kolébání půlválce není tlumeno odporovými silami a že půlválec koná harmonický pohyb.
Vztahy pro okamžitou úhlovou výchylku z rovnovážné polohy a okamžitou úhlovou rychlost budou obdobné jako například pro kmitání kuličky na pružině. Napište je.
Nápověda b) 2
K dalšímu řešení použijte zákon zachování mechanické energie. Napište, jakou mechanickou energii má válec, pokud ho vychýlíme z rovnovážné polohy, a jakou energii má při průchodu rovnovážnou polohou. Nezapomeňte zvolit hladinu nulové potenciální energie.
Celkové řešení
a)Steinerova věta říká, že známe-li JT, moment setrvačnosti tělesa o hmotnosti m při otáčení kolem osy procházející těžištěm, dá se vyjádřit moment setrvačnosti tělesa při otáčení kolem rovnoběžné osy ve vzdálenosti d takto:
\[J=J_\mathrm{T}+md^2\,.\]Moment setrvačnosti válce při otáčení podle osy procházející středy podstav je:
\[J=\frac{1}{2}mr^2\,.\]Kdybychom k našemu půlválci přiklopili ještě jeden, dostali bychom válec o momentu setrvačnosti vůči rotační ose symetrie \(\frac{1}{2}2mr^2\).
Náš půlválec má proti takovému tělesu poloviční hmotnost, ale hmotu má od řečené osy rozloženou ve stejném poměru, proto:
\[J_\mathrm{S}=\frac{1}{2}mr^2\,.\]Podle Steinerovy věty platí:
\[J_\mathrm{S}=J_\mathrm{T}+mp^2\,.\]Označme hledaný moment setrvačnosti JH. Podle Steinerovy věty platí:
\[J_\mathrm{H}=J_\mathrm{T}+m(r-p)^2\,.\]Dosadíme postupně za JT, JS a p:
\[J_\mathrm{H} = J_\mathrm{S} - mp^2 + mr^2 - 2mrp + mp^2\,,\] \[J_\mathrm{H} = J_\mathrm{S}+ mr^2-2mrp=\frac{1}{2}mr^2+mr^2-2mr\frac{4r}{3\pi}\,,\] \[J_\mathrm{H}=mr^2(\frac{3}{2}-\frac{8}{3\pi})\,.\tag{1}\] b)Předpokládejme, že kolébání půlválce není tlumeno odporovými silami a že půlválec koná harmonický pohyb.
Pro okamžitou výchylku z rovnovážné polohy α platí:
\[\alpha (t)=\alpha_0\cos\omega t\,,\]kde \(\omega=2\pi f = \frac{2\pi}{T}.\)
Derivací podle t získáme okamžitou úhlovou rychlost ω:
\[\omega (t) = - \alpha_0\omega\sin\omega t\,.\] Označíme: \[\omega_\mathrm{m}=\omega\alpha_0\,.\tag{2}\]K dalšímu řešení použijeme zákon zachování mechanické energie. Napíšeme, jakou mechanickou energii má válec, když ho vychýlíme z rovnovážné polohy, a jakou energii má při průchodu rovnovážnou polohou. Hladinu nulové potenciální energie zvolíme v těžišti v rovnovážné poloze.
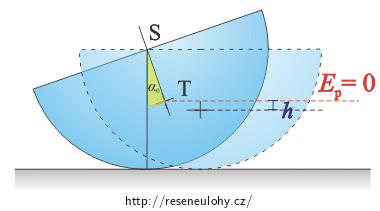
Při vychýlení zvedneme těžiště o výšku h, která je rozdílem vzdálenosti bodů S a T (tedy p) a kolmého průmětu této vzdálenosti po vychýlení půlválce, pcosα0:
\[h=p-p\cos\alpha_0\dot{=}p(1-(1-\frac{\alpha^2}{2}))=\frac{2r\alpha^2}{3\pi}\,.\tag{3}\]V okamžiku vychýlení má válec nulovou kinetickou energii a potenciální energie je rovna:
\[E_\mathrm{p1}=mgh=\frac{2mgr\alpha^2}{3\pi}\,.\]Při průchodu rovnovážnou polohou je potenciální energie rovna nule a kinetická energie je rovna:
\[E_\mathrm{k2} = \frac{1}{2}J\omega_\mathrm{m}^2\,.\]Podle zákona zachování energie platí:
\[E_\mathrm{k2} = E_\mathrm{p1} \,,\] \[\frac{1}{2}J_\mathrm{H}\omega_\mathrm{m}^2=mgh\,.\]Dosadíme za \(J_\mathrm{H}, \omega_\mathrm{m}, h\) ze vztahů (1), (2), (3):
\[\frac{1}{2}mr^2(\frac{3}{2}-\frac{8}{3\pi})(\omega\alpha_0)^2 = mg\frac{2r\alpha_0^2}{3\pi}\,.\]Upravíme a vyjádříme ω:
\[\frac{1}{2}r(\frac{3}{2}-\frac{8}{3\pi})\omega^2=g\frac{2}{3\pi}\,,\] \[\omega^2=\frac{4g}{3\pi r(\frac{3}{2}-\frac{8}{3\pi})}\,,\] \[\omega^2=\frac{8g}{ r(9\pi-16)}\,.\]A protože \(\omega=\frac{2\pi}{T}\), tak:
\[T=2\pi\sqrt{\frac{r(9\pi-16)}{8g}}\,,\] \[T=\pi\sqrt{\frac{r(9\pi-16)}{2g}}\,.\]Odpověď
a) Hledaný moment setrvačnosti je:
\[J_\mathrm{H}=mr^2(\frac{3}{2}-\frac{8}{3\pi})\,.\]b) Půlválec kmitá s periodou:
\[T=\pi\sqrt{\frac{r(9\pi-16)}{2g}}\,.\]


