Střela a tyč II
Úloha číslo: 2209
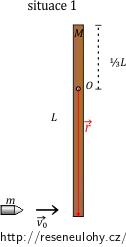
Vodorovně letící střela o hmotnosti \(m\) a rychlosti \(\vec {v_{0}}\) zasáhne dolní konec visící dřevěné tyče délky \(L\) a hmotnosti \(M\) a uvázne v ní. Tyč je volně otáčivá kolem vodorovné osy procházející ve vzdálenosti \(\frac{1}{3}L\) od jejího horního konce.
a) Určete moment setrvačnosti tyče vzhledem k ose otáčení.
b) Vypočtěte úhlovou rychlost, se kterou se tyč začne otáčet.
c) Vypočtěte poměr změny vnitřní energie soustavy střely a tyče \(\Delta U\) ku počáteční kinetické energii soustavy \(E_\mathrm{k_{0}}\).
Rozbor
V celé úloze předpokládáme, že se střela do tyče zaryje po nárazu velmi rychle a pak se tyč se střelou začne otáčet úhlovou rychlostí, kterou hledáme. Budeme využívat zákon zachování momentu hybnosti. Zvolíme dvě situace, první těsně před nárazem střely do tyče, druhou těsně po nárazu. Celkový moment hybnosti soustavy střely a tyče v těchto situacích si zapíšeme. Z rovnosti velikostí obou momentů hybnosti vyjádříme hledanou úhlovou rychlost.
Při nárazu se střela i tyč zahřívají a deformují, mechanická energie tedy není v tomto případě zachována. Z rozdílu celkové mechanické energie soustavy střely a tyče před nárazem a po něm určíme změnu vnitřní energie soustavy.
Nápověda a)
Při určování momentu setrvačnosti tyče vyjdeme z následujícího vztahu
\[J_\mathrm{tyč} = \int_V{\rho r^2}\,\mathrm{d}V,\]
kde r je vzdálenost elementu \(\mathrm{d}V\) od osy otáčení a \(\rho\) hustota tyče.
Zamyslete se, jak jej lze zjednodušit, jestliže předpokládáme, že tyč je homogenní a tenká. Jaké meze by měl integrál, pokud by osa procházela koncem tyče? Jak se integrační meze změní v případě, že je osa umístěna v \(\frac{1}{3}\) délky tyče?
Nápověda b)
Předpokládejme, že se střela do tyče po nárazu zaryje velmi rychle a pak se začnou společně pohybovat. K řešení využijeme jeden ze zákonů zachování. Jaká veličina se v tomto případě zachovává?
Nápověda c)
Zapište si, čemu je rovna počáteční mechanická energie soustavy střely a tyče před nárazem. Stejně tak pro situaci těsně po nárazu. Zamyslete se, zda budou mechanické energie před nárazem a po něm stejně velké či ne. Jak vyjádříte změnu vnitřní energie soustavy?
Řesení a)
Moment setrvačnosti určíme z integrálu
\[ J_\mathrm{tyč} = \int_V{\rho r^2}\,\mathrm{d}V, \]
kde \(r\) označuje vzdálenost elementu dV od osy otáčení. Tyč je homogenní a nekonečně tenká, stačí tedy integrál počítat v jednorozměrném prostoru. Integrál můžeme upravit do tvaru
\[ J_\mathrm{tyč} = \int{\lambda r^2}\,\mathrm{d}r, \tag{1}\]
kde \(\lambda\) je délková hustota (která charakterizuje rozložení celkové hmoty tyče \(M\) na celé její délce \(L\)). Protože uvažujeme tyč homogenní, platí
\[ \lambda = \frac{M}{L} . \tag{2}\]
Víme, že osa otáčení je umístěna ve vzdálenosti \(\frac{1}{3}L\) od horního konce tyče. Při výpočtu budeme integrovat v mezích od \(−\frac{1}{3}L\) do \(\frac{2}{3}L\), abychom zahrnuli celou délku tyče.

Dosazením výrazu (2) do integrálu (1) a přidáním mezí získáme určitý integrál pro výpočet momentu setrvačnosti tyče \(J_\mathrm{tyč}\):
\[ J_\mathrm{tyč} = \int_{−\frac{L}{3}}^{\frac{2}{3}L}{\frac{M}{L} r^2}\,\mathrm{d}r =\frac{M}{L} \int_{−\frac{L}{3}}^{\frac{2}{3}L}{ r^2}\,\mathrm{d}r = \frac{M}{L} \left[\frac{r^3}{3}\right]_{−\frac{L}{3}}^{\frac{2}{3}L} = \frac{M}{L}\left[\frac{8}{27{\cdot} 3}L^3−\left(−\frac{1}{27{\cdot} 3}L^3\right)\right] =ML^2 \left(\frac{9}{27 {\cdot} 3}\right). \]
Zkrácením zlomku v získaném výrazu dostaneme výsledek:
\[ J_\mathrm{tyč} = \frac{1}{9}ML^2. \]
Poznámka: Pro podrobnější postup odvození integrálu se podívejte na úlohu Střela a tyč I nebo Moment setrvačnosti tyče.
Řešení b)
K určení úhlové rychlosti \(\vec \omega\) využijeme zákon zachování momentu hybnosti. Uvažujme dvě situace, ve kterých musí být celkový moment hybnosti soustavy střely a tyče stejný.
Moment hybnosti hmotného bodu \(\vec L\) vzhledem k bodu O je určen vektorovým součinem
\[ \vec L = \vec {r}×\vec{p}, \]
kde \(\vec r\) je polohový vektor směřující od bodu O ke konci tyče, kam se zarývá střela, a \(\vec p\) je vektor hybnosti.
Pro velikost vektorového součinu platí
\[L = rp\sin\varphi \,,\]kde φ je úhel sevřený oběma vektory.
Vektor momentu hybnosti je kolmý k rovině určené vektory \(\vec{r}\) a \(\vec{p}\). Jeho orientaci lze určit pravidlem pravé ruky: prsty dáme tak, aby směřovaly od \(\vec{r}\) k \(\vec{p}\), napnutý palec pak ukazuje směr vektoru \(\vec{L}\). Vektor \(\vec p\) má stejný směr jako rychlost \(\vec {v_0}\).
Pro moment hybnosti tuhého tělesa vzhledem k pevné ose otáčení platí
\[\vec{L} = J\vec{\omega}\,,\]kde J je moment setrvačnosti tělesa vzhledem k pevné ose otáčení a \(\vec{\omega}\) úhlová rychlost otáčení.
Pro velikost momentu hybnosti platí
\[L = J\omega\,.\]Směr vektoru momentu hybnosti je daný směrem vektoru úhlové rychlosti \(\vec{\omega}\).
Moment hybnosti budeme určovat vzhledem k bodu závěsu tyče O.
V první situaci je tyč v klidu, celkový moment hybnosti soustavy střely a tyče se bude rovnat momentu hybnosti samotné střely. Střela se pohybuje rychlostí \(\vec {v_0}\) kolmo k tyči. Moment hybnosti v první situaci je
\[ \vec {L_{1}} = \vec {r}×\vec{p}= \vec {r}×\left (m\vec{v_{0}}\right ). \]
Velikost polohového vektoru je rovna \(\frac{2}{3}\) délky tyče \(L\). Víme, že sinus pravého úhlu sevřeného vektory \(\vec r\) a \(\vec p\) je roven 1. Pro velikost momentu hybnosti tedy platí
\[ L_{1} = \frac{2}{3}Lp = \frac{2}{3}mv_{0}L . \tag{3}\]
V druhé situaci musíme také započítat rotační pohyb tyče kolem osy. Moment hybnosti \(\vec L_{2}\) určíme pomocí součinu momentu setrvačnosti celého tělesa \(J\) a jeho úhlové rychlosti \(\vec{\omega}\). Na celkovém momentu setrvačnosti se podílí tyč (moment setrvačnosti \(J_\mathrm{tyč}\) jsme určili v předchozí části úlohy) a střela, kterou považujeme za hmotný bod ve vzdálenosti \(\frac{2}{3}L\) od osy otáčení. Střela i tyč se pohybují stejnou úhlovou rychlostí, jejich momenty setrvačnosti tedy můžeme sečíst a získáme celkový moment setrvačnosti:
\[ J = J_\mathrm{tyč} + J_\mathrm{střela} = \frac{1}{9}ML^2 + m\left(\frac{2}{3}L\right)^2. \tag{4}\]
Pro moment hybnosti \(\vec L_{2}\) tedy platí
\[ \vec{L_{2}} = J\vec{\omega} = \left(\frac{1}{9}ML^2 + m\left(\frac{2}{3}L\right)^2\right)\vec{\omega}. \]
A pro jeho velikost
\[ L_{2} = J\omega = \left(\frac{1}{9}ML^2 + m\left(\frac{2}{3}L\right)^2\right){\omega}. \tag{5}\]
Podle zákona zachování momentu hybnosti dostáváme rovnost vztahů (3) a (5):
\[ L_1=L_2, \]
\[ \frac{2}{3}mv_{0}L = \left(\frac{1}{9}ML^2 + m\frac{4}{9}L^2\right)\omega. \]
Postupně vyjádříme úhlovou rychlost \(\omega\):
\[ \frac{2}{3}mv_{0} = \left(\frac{1}{9}M+ m\frac{4}{9}\right)L\omega, \]
\[ 2mv_{0} = \left(\frac{1}{3}M+ m\frac{4}{3}\right)L\omega, \]
\[ \omega = \frac{2mv_{0}}{\left(\frac{1}{3}M + \frac{4}{3}m\right)L}. \]
Výraz upravíme a získáváme
\[ \omega = \frac{6mv_{0}}{\left(M + 4m\right)L}. \]
Řešení c)
Postup řešení poslední části úlohy je stejný jako v poslední sekci úlohy Střela a tyč I, kde si můžete pročíst podrobnější vysvětlení.
Chceme určit poměr změny vnitřní energie soustavy tyče a střely ku její počáteční kinetické energii. Počáteční kinetická energie soustavy je stejná jako počáteční kinetická energie střely:
\[ E_\mathrm{k_{0}} = \frac{1}{2}mv_{0}^2. \]
Změnu vnitřní energie \(\Delta U\) určíme jako rozdíl počáteční kinetické energie soustavy \(E_\mathrm{k_{0}}\) a energie rotačního pohybu \(E_\mathrm{k}\), kde
\[ E_\mathrm{k} = \frac{1}{2}J\omega^2. \]
Celkový moment setrvačnosti pro tyč se střelou \(J\) jsme určili v předchozí části úlohy, jedná se o vztah (4).
Známe vše potřebné k určení hledaného poměru. Dosadíme:
\[ \frac{\Delta U}{E_{k_\mathrm{0}}} =\frac{E_\mathrm{k_{0}} −E_\mathrm{k}}{E_\mathrm{k_{0}}} =\frac{\frac{1}{2}mv_{0}^2−\frac{1}{2}\left(\frac{1}{9}ML^2+\frac{4}{9}mL^2\right) \omega^2}{\frac{1}{2}mv_{0}^2}. \]
Z předchozí části úlohy dosadíme za úhlovou rychlost \(\omega\) a výraz upravíme:
\[ \frac{\Delta U}{E_\mathrm{k_{0}}}=\frac{\frac{1}{2}mv_{0}^2−\frac{1}{18}L^2\left(M+4m\right) \frac{36m^2v_{0}^2}{\left(M + 4m\right)^2L^2}}{\frac{1}{2}mv_{0}^2} = \frac{\frac{1}{2}m−\frac{2m^2}{\left(M + 4m\right)}}{\frac{1}{2}m} = 1−\frac{4m}{\left(M + 4m\right)}. \]
Získáváme poměr
\[ \frac{\Delta U}{E_\mathrm{k_{0}}}= \frac{M}{\left(M + 4m\right)}. \]
Odpověď a)
Moment setrvačnosti tyče vzhledem k vodorovné ose otáčení procházející v jedné třetině délky tyče je
\[ J_\mathrm{tyč} = \frac{1}{9}ML^2. \]
Odpověď b)
Úhlová rychlost, se kterou se začne tyč se střelou otáčet, je
\[ \omega = \frac{6mv_{0}}{\left(M + 4m\right)L}. \]
Odpověď c)
Poměr změny vnitřní energie soustavy střely a tyče \(\Delta U\) ku počáteční kinetické energii soustavy \(E_\mathrm{k_{0}}\) je
\[ \frac{\Delta U}{E_\mathrm{k_{0}}} =\frac{M}{\left(M + 4m\right)}. \]
Moment setrvačnosti tyče jinak
Moment setrvačnosti tyče z první části této úlohy lze také řešit pomocí Steinerovy věty.
Vyjdeme z momentu setrvačnosti tyče vzhledem k ose procházející hmotným středem tyče
\[J_{1} = \frac{1}{12}ML^2.\]
Steinerova věta nám říká, že moment setrvačnosti tělesa vzhledem k ose rovnoběžné s osou procházející hmotným středem tělesa určíme jako součet momentu setrvačnosti vzhledem k ose procházející hmotným středem (tj. \(J_{1}\)) a čtverce polohového vektoru \(\vec{r_{s}}\), který určuje vzdálenost obou os, násobeného hmotností tělesa:
\[ J_{2} = J_{1} + M\left(\vec {r_{s}}\right)^2. \]
V našem případě, jak je vidět na obrázku níže, je vzdálenost \(\left|\vec{r_{s}}\right|\) rovna \(\frac{1}{6}L\).
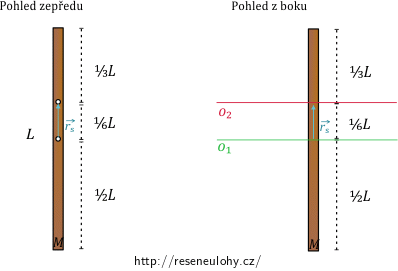
Získáváme
\[J_{2} = \frac{1}{12}ML^2 + M\left(\frac{1}{6}L\right)^2 = \frac{1}{12}ML^2+\frac{1}{36}ML^2 = \left(\frac{3+1}{36}\right)ML^2 = \frac{1}{9}ML^2.\]
Dostali jsme stejný výsledek jako v řešení pomocí integrálu.
Jednodušší úloha
Chcete-li řešit podobnou, o něco jednodušší úlohu, podívejte se na Střela a tyč I.



