Cyklista jede do kopce
Úloha číslo: 144
Cyklista jede do kopce se stoupáním 5 % stálou rychlostí 27 km·h−1. Odporová síla vzduchu má velikost Fodp = kv2, kde číselná hodnota {k} = 0,3, přičemž rychlost uvádíme v jednotkách m·s−1 a sílu v newtonech. Hmotnost cyklisty i s kolem je 70 kg. Valivý odpor neuvažujte.
Jak velkou silou musí strkat do kola silnice, aby jelo rovnoměrným pohybem?
Jakou práci musí cyklista vykonat na trase 1 200 m? Jaký je výkon cyklisty při jízdě? Předpokládejte, že nedochází ke ztrátám mechanické energie.
Zápis
α = 5° stoupání kopce v = 27 km·h−1 stálá velikost rychlosti cyklisty Fodp = k·v2 velikost odporové síly vzduchu {k} = 0,3 konstanta m = 70 kg hmotnost cyklisty s kolem s = 1200 m vzdálenost, kterou cyklista ujel F = ? velikost síly, kterou silnice strká do kola W = ? práce, kterou cyklista vykonal na dráze s P = ? výkon cyklisty při jizdě do kopce Nápověda 1 – působící síly
Nakreslete si obrázek včetně působících sil. Co můžete říct o výsledné síle působící na cyklistu, který jede stálou rychlostí?
Nápověda 2 – práce a výkon cyklisty
Předpokládáme-li, že nedochází ke ztrátám mechanické energie, je práce vykonaná cyklistou rovna práci, již vykoná síla, kterou silnice posunuje kolo směrem vpřed. Síla, kterou působí silnice na kolo, je konstantní. Jakou práci vykoná na dané dráze?
Jak můžeme spočítat výkon, známe-li sílu a rychlost?
Číselný výpočet
Dáno:
\[m\,=\,70\, \mathrm{kg},\] \[g\,=\,9{,}81\, \mathrm{m \cdot s^{-2}},\] \[\sin\alpha\,=\,5\,\%\,=\,0{,}05,\] \[k\,=\,0{,}3\,\mathrm{kgm^{-1}},\] \[v\,=\,27\, \mathrm{km \cdot h^{-1}}\,=\,7{,}5\,\mathrm{m \cdot s^{-1}}.\]Hledáme:
\[F\,=\,?,\] \[W\,=\,?, \] \[P\,=\,?.\]
\[F\,=\,F_\mathrm{odp}+F_\mathrm{g}\sin\alpha\,=\,kv^{2}+mg\sin\alpha,\] \[F\,=\,(0{,}3{\cdot}7{,}5^{2}+70{\cdot}9{,}81{\cdot}0{,}05)\,\mathrm{N},\] \[F\,=\,51{,}2\, \mathrm{N},\] \[W\,=\,Fs\,=\,51{,}2\,\cdot\,1\,200\,\mathrm{J},\] \[W\,=\,61\,440\, \mathrm{J}\,\,\dot=\,61{,}4\ \mathrm{kJ},\] \[P\,=\,(F_\mathrm{odp}+F_\mathrm{g}\sin\alpha)v\,=\,(kv^2+mg\sin\alpha)v,\] \[P\,=\,(0{,}3{\cdot}7{,}5^{2}+70{\cdot}9{,}81{\cdot}0{,}05)\cdot7{,}5\,\mathrm{W}\,=\,51{,}2{\cdot}7{,}5\,\mathrm{W},\] \[P\,=\,384\, \mathrm{W}.\]Celkové řešení
Výpočet síly:
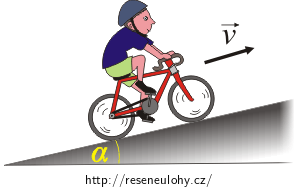
Pro zjednodušení si představíme cyklistu s kolem jako jedno těleso. Zakreslíme si do obrázku všechny působící síly.

\(\vec{F}_\mathrm{g}\)…tíhová síla
\(\vec{N}\)…síla, kterou do kola tlačí silnice
\(\vec{F}_\mathrm{odp}\)…odporová síla
\(\vec{F}\)…síla, kterou do kola strká silnice
Výsledná síla působící na cyklistu musí být při rovnoměrném přímočarém pohybu rovna nule:
\[\vec{F}_\mathrm{g}+\vec{F}_\mathrm{odp}+\vec{N}+\vec{F}\,=\,0.\]Zvolíme soustavu souřadnic podle obrázku a rovnici přepíšeme skalárně:
\[x:\qquad -F_\mathrm{g}\sin\alpha-F_\mathrm{odp}+F\,=\,0,\tag{1}\] \[y:\qquad N-F_\mathrm{g}\cos\alpha\,=\,0.\]Hledanou sílu F vyjádříme z rovnice (1):
\[F\,=\,F_\mathrm{g}\sin\alpha+F_\mathrm{odp}\,=\,mg\sin\alpha+kv^2.\tag{2}\]Vyjádříme \(\sin\alpha\) pomocí známého stoupání. Stoupání 5 % znamená, že na 100 m stoupne silnice o 5 m (viz obrázek dole).
\[\sin\alpha\,\,\frac{5}{100}\,=\,0{,}05\]\[F\,=\,kv^2+mg\sin\alpha,\tag{3}\] \[F_\mathrm{c}\,=\,0{,}3{\cdot}7{,}5^{2}\,+\,70{\cdot}9{,}81{\cdot}0{,}05\,\mathrm{N},\] \[F_\mathrm{c}\,=\,51{,}2\, \mathrm{N}.\]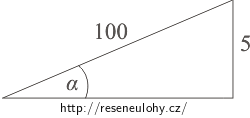
Výpočet práce:
Síla je konstantní a působí ve směru posunutí cyklisty, takže práci spočítáme podle vztahu:
\[W\,=\,Fs,\]W…práce cyklisty,
F…síla, kterou strká do kola silnice,
s…dráha, kterou cyklista ujede.
Za výslednou sílu dosadíme ze vztahu (2)
\[W\,=\,(F_\mathrm{odp}+F_\mathrm{g}\alpha)s,\] \[W\,=\,(kv^2+mg\sin\alpha)s,\] \[W\,=\,(0{,}3{\cdot}7{,}5^{2}+70{\cdot}9{,}81{\cdot}0{,}05)\cdot1\,200\,\mathrm{J},\] \[W\,=\,51{,}2\,\cdot\, 1\,200\,\mathrm{J},\] \[W\,=\,61\,440\, J\,\,\dot=\,61{,}4\ \mathrm{kJ}.\]Výpočet výkonu:
Pro okamžitý výkon platí:
\[P\,=\,\frac{dW}{dt}\,=\,\frac {dF\cdot s}{dt}\,=\,F\cdot\frac {ds}{dt}\,=\,F\cdot v,\]P…okamžitý výkon,
F…síla, kterou strká do kola silnice,
v…rychlost cyklisty.
Za sílu F dosadíme ze vztahu (2):
\[P\,=\,(F_\mathrm{odp}+F_\mathrm{g}\sin\alpha)\cdot v,\] \[P\,=\,(kv^2+mg\sin\alpha)v,\] \[P\,=\,(0{,}3{\cdot}7{,}5^{2}+70{\cdot}9{,}81{\cdot}0{,}05)\cdot7{,}5\,\mathrm{W},\] \[P\,=\,51{,}2{\cdot}7{,}5\,\mathrm{W},\] \[P\,=\,384\, \mathrm{W}.\]Odpověď:
Síla, kterou silnice strká do kola, je rovna \[F\,=\,51{,}2\, \mathrm{N}.\]
Na dráze 1 200 m musí cyklista vykonat práci \[W\,\,\dot=\,61{,}4\ \mathrm{kJ}.\]
Výkon cyklisty při jizdě do kopce je \[P\,=\,384\, \mathrm{W}.\]
Odpověď
Síla, kterou silnice strká do kola, je rovna \[F\,=\,kv^2+mg\sin\alpha\,=\,51{,}2\, \mathrm{N}.\]
Na dráze 1200 m musí cyklista vykonat práci \[W\,=\,\left(kv^2+mg\sin\alpha\right)s\,\,\dot=\,61{,}4\ \mathrm{kJ}.\]
Výkon cyklisty při jizdě do kopce je \[P\,=\,\left(kv^2+mg\sin\alpha\right)v\,=\,384\, \mathrm{W}.\]





