Dělník roztahuje bednu
Úloha číslo: 90
Dělník roztahuje bednu o hmotnosti 50 kg po hladké vodorovné podlaze. Působí na ni přitom silou o velikosti 210 N pod úhlem 20° vzhledem k podlaze. Zjištěte, jakou práci vykonaly při posunutí bedny o 0,5 m následující síly:
a) síla, kterou působí dělník na bednu,
b) tíhová síla,
c) tlaková síla, jíž působí na bednu podlaha.
d) Jaká je celková práce všech sil působících na bednu?
Tření bedny o podlahu neuvažujeme.
Zápis
m = 50 kg hmotnost bedny F = 210 N velikost síly, kterou dělník roztahuje bednu α = 20° úhel, který svírá vektor síly \(\vec{F}\) s vektorem posunutí s = 0,5 m dráha, o kterou byla bedna posunuta W = ? práce, kterou vykoná síla \(\vec{F}\) Wg = ? práce, kterou vykoná tíhová síla WN = ? práce, kterou vykoná tlaková síla WC = ? celková práce Nápověda 1 – práce dělníka
Nakreslete si obrázek a do něho působící síly.
Sílu, kterou působí dělník na bednu, považujeme za konstantní. Jaký je vztah pro práci konstantní síly?
Nápověda 2 – práce tíhové síly
Ve vztahu pro práci konstantní síly (1) nahraďte sílu \(\vec{F}\) vztahem pro tíhovou sílu \(\vec{F}_\mathrm{g}\). Uvědomte si, jaký úhel svírá tíhová síla s vektorem posunutí.
Nápověda 3 – práce tlakové síly
Dosaďte do vztahu pro práci konstantní síly (1) místo síly \(\vec{F}\) tlakovou sílu \(\vec{N}\).
Nápověda 4 – celková práce
Celkovou práci spočítáte jako součet prací vykonaných jednotlivými silami.
Číselný výpočet
a)
\[F\,=\, 210\, \mathrm{N}\] \[s\,=\, 0{,}5 \,\mathrm{m}\] \[\alpha\,=\,20^{\circ}\]
\[W\,=\,Fs\cos\alpha\] \[W\,=\,210{\cdot}0{,}5\cdot\cos20^{\circ}\,\mathrm{J}\] \[W\,=\,105{\cdot}0{,}94\,\mathrm{J}\] \[W\,=\,98{,}7\,\mathrm{J}\dot=\, 99\,\mathrm{J}\]b)
Vektor tíhové síly svírá s vektorem posunutí úhel 90° čili práce, kterou tato síla vykoná, je nulová.
c)
Vektor tlakové síly svírá s vektorem posunutí opět úhel 90°. Práce, kterou vykoná tato síla, je nulová.
d)
\[W\,=\,98{,}7\,\mathrm{J}\] \[W_\mathrm{g}\,=\,0\,\mathrm{J}\] \[W_\mathrm{N}\,=\,0\,\mathrm{J}\] \[W_\mathrm{c}\,=\,W+W_\mathrm{g}+W_\mathrm{N}\] \[W_\mathrm{c}\,=\,98{,}7\,\mathrm{J} \dot=\, 99\,\mathrm{J}\]Odpověď
a) Práce vykonaná dělníkem je rovna \(W\,=\,Fs\cos\alpha\,\dot=\, 99\,\mathrm{J}\).
b) Práce vykonaná tíhovou sílou Wg je rovna nule.
c) Práce vykonaná tlakovou sílou WN je rovna nule.
d) Celková práce je rovna \(W_\mathrm{c}\,=\,W+W_\mathrm{g}+W_\mathrm{N}\,=\,Fs\cos\alpha\,\dot=\, 99\,\mathrm{J}\).
Komentář
Bedna se při roztahování pohybuje rovnoměrně zrychleně.
V úloze řešíme idealizovaný případ, kdy neuvažujeme působení třecí síly, která by v realné situaci působila proti směru pohybu bedny.
Celkové řešení bodu a) – práce dělníka
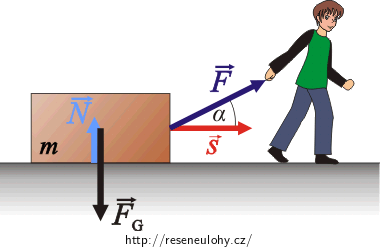
\(\vec{F}\) … síla, kterou působí dělník na bednu
\(\vec{N}\) … síla, kterou působí podlaha na bednu
\(\vec{F}_\mathrm{g}\) … tíhová síla
V případě, že je působící síla konstantní, spočítáme práci jako skalární součin vektoru působící síly a vektoru posunutí:
\[W\,=\,\vec{F}\cdot\vec{s}.\]\(W\) … vykonaná práce
\(\vec{F}\) … vektor síly, kterou působí na bednu dělník
\(\vec{s}\) … vektor posunutí
Pro skalární součin platí:
\[W\,=\,Fs\cos \alpha,\tag{1}\] \[F= 210 \,\mathrm{N},\] \[s= 0{,}5\,\mathrm{m},\] \[\alpha=20^{\circ},\] \[W\,=\,Fs\cos\alpha\,=\,210{\cdot}0{,}5\cdot\cos20^{\circ}\,\mathrm{J}\,=\,105{\cdot}0{,}94\,\mathrm{J1},\] \[W\,=\,98{,}7\,\mathrm{J}\dot=\, 99\,\mathrm{J}.\]Odpověď: Práce vykonaná dělníkem je rovna \[W\,=\,Fs\cos\alpha\,\dot=\, 99\,\mathrm{J}.\]
Celkové řešení bodu b) – práce tíhové síly
Ve vztahu pro práci konstantní síly nahradíme sílu \(\vec{F}\) vztahem pro tíhovou sílu \(\vec{F}_\mathrm{g}\):
\[W_\mathrm{g}\,=\,\vec{F}_\mathrm{g}\cdot\vec {s},\] \[W_\mathrm{g}\,=\,m\cdot\vec{g}\cdot\vec{s},\] \[W_\mathrm{g}\,=\,mgs\cos \alpha^{'}.\]\(W_\mathrm{g}\) … práce, kterou vykoná tíhová síla
\(\vec{F}_\mathrm{g}\) … tíhová síla
\(m\) … hmotnost bedny
\(\vec{g}\) … vektor tíhového zrychlení
\(\vec{s}\) … vektor posunutí
\(\alpha^{'}\) … úhel, který svírá vektor tíhové síly s vektorem posunutí, \(\alpha^{'}=90^{\circ}\)
\[\cos\alpha^{'}\,=\,\cos90^{\circ}\,=\,0\] \[W_\mathrm{g}\,=\,m\cdot g\cdot s\cdot 0\,=\,0\]Odpověď: Práce vykonaná tíhovou sílou je rovna nule.
Celkové řešení bodu c) – práce tlakové síly
Dosaďte do vztahu pro práci konstantní síly (1) místo síly \(\vec{F}\) tlakovou sílu \(\vec{N}\):
\[W_\mathrm{N}\,=\,\vec{N}\cdot\vec{s},\] \[W_\mathrm{N}\,=\,Ns\cos\alpha^{''}.\]\(W_\mathrm{N}\) … práce, kterou vykoná tlaková síla
\(\vec{N}\) … vektor tlakové síly
\(\vec{s}\) … vektor posunutí
\(\alpha^{''}\) … úhel, který svírá vektor tlakové síly s vektorem posunutí
Vektor tlakové síly svíra s vektorem posunutí opět úhel 90°. Práce, kterou vykoná tato síla, je nulová:
\[\cos\alpha^{''}\,=\,\cos90^{\circ}\,=\,0,\] \[W_\mathrm{N}\,=\,m\cdot g\cdot s\cdot 0\,=\,0.\]Odpověď: Práce vykonaná tlakovou sílou je rovna nule.
Celkové řešení bodu d) – celková práce
Celkovou práci spočítáme jako součet prací vykonaných jednotlivými silami:
\[W_\mathrm{c}\,=\,W+W_\mathrm{g}+W_\mathrm{N}.\]\(W_\mathrm{c}\) … celková práce
\(W\) … práce, kterou vykoná síla \(\vec{F}\)
\(W_\mathrm{g}\) … práce, kterou vykoná tíhová síla \(\vec{F}_\mathrm{g}\)
\(W_\mathrm{N}\) … práce, kterou vykoná tlaková síla \(\vec{N}\)
\[W\,=\,Fs\cos\alpha\] \[W_\mathrm{g}\,=\,0\,\mathrm{J}\] \[W_\mathrm{N}\,=\,0\,\mathrm{J}\] \[W_\mathrm{c}\,=\,W+W_\mathrm{g}+W_\mathrm{N}=Fs\cos\alpha\] \[W_\mathrm{c}\,=\,98{,}7\,\mathrm{J}\dot=\, 99\,\mathrm{J}\]Odpověď: Celková práce je rovna \(W_\mathrm{c}\,=\,W+W_\mathrm{g}+W_\mathrm{N}\,=\,\dot=\, 99\,\mathrm{J}\).





