Moment síly a vektorový součin
Úloha číslo: 544
Na obrázku je klaun zavírající okno. Určete velikost a směr vektoru momentu vodorovné síly \(\vec F\), kterou klaun na okno působí vzhledem k ose závěsů.
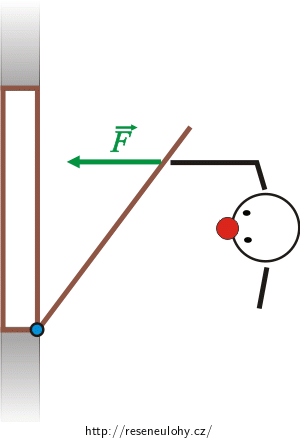
Moment síly jako vektor
Moment síly, jak ho známe ze ZŠ, je číslo s jednotkou (skalární veličina), které získáme vynásobením velikosti síly s ramenem síly, což je kolmá vzdálenost mezi vektorovou přímkou síly a osou otáčení.
Obecně je moment síly vektorová veličina definovaná vztahem:
\[\vec M=\vec r \times \vec F\,,\]kde \(\vec F\) je působící síla,
\(\vec r\) je polohový vektor, jenž začíná v bodě, vůči kterému moment síly určujeme a míří do působiště síly,
a znak \(\times\) značí vektorový součin.
Polohový vektor \(\vec r\) zakreslíme do obrázku.
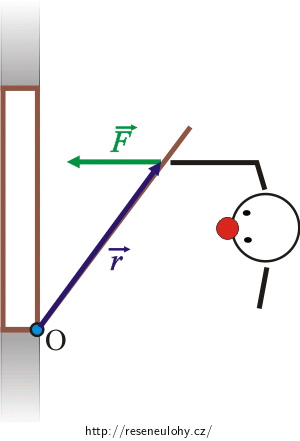
Vektor \(\vec r\) je kolmý na osu, tedy vodorovný.
Velikost momentu síly
Pokud vektory \(\vec r\) a \(\vec F\) svírají obecný úhel φ, je velikost momentu síly rovna:
\[M=rF\sin\varphi\,.\]V případě, že jsou vektory \(\vec r\) a \(\vec F\) kolmé, je \(\sin\varphi = 1\) a pro velikost momentu síly platí:
\[M=rF\,.\]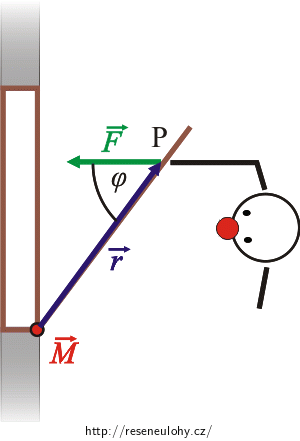
Geometricky to lze chápat tak, že velikost výsledného vektoru je rovna rovnoběžníku vymezeného vektory \(\vec F\) a \(\vec r\). Speciálně pokud spolu vektory svírají nulový úhel, je výsledkem nulový vektor.
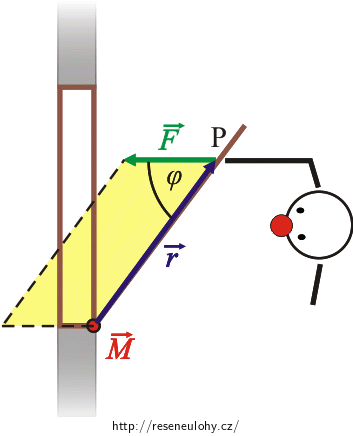
Směr momentu síly
Výsledný vektor momentu síly je vždy kolmý na rovinu, ve které leží oba původní vektory.
Orientace momentu síly
Vektory musí tvořit tzv. pravotočivou bázi. To je tvar, který dostanete z prvních tří prstů pravé ruky, když natáhnete palec, ukazováček a prostředník kolmý na oba dva.
V našem případě je \(\vec r\) první vektor (palec), \(\vec F\) druhý vektor (ukazovák) a třetím je \(\vec M\) (prostředník).
Orientaci můžeme určit také pomocí pravidla pravé ruky následujícím způsobem: prsty dáme tak, aby směřovaly od \(\vec{r}\) k \(\vec{F}\), napnutý palec pak ukazuje směr vektoru \(\vec{M}\).
Nebude asi žádným překvapením, že použijete-li levou ruku, získáte bázi jinou, levotočivou.Řešení
Když známe oba vektory \(\vec r\) i \(\vec F\), použijeme znalosti o vektorovém součinu uvedené výše.
Velikost vektoru momentu síly je \(M = Fr\sin \varphi\), kde φ je úhel sevřený vektory. Díky vlastnostem funkce sin je jedno, který z úhlů mezi vektory vezmeme. Na obrázku odpovídá ploše vyšrafovaného rovnoběžníku.
Směr vektoru \(\vec M\) je kolmý na \(\vec r\) i \(\vec F\), tedy rovnoběžný s osou otáčení.
Abychom určili orientaci, použijeme pravidlo pravé ruky. \(\vec r\) je ve vektorovém součinu první, odpovídá tedy prvnímu prstu, \(\vec F\) je druhý, dostane tedy druhý prst a \(\vec M\) třetí.
Potažmo prsty pravé ruky míří od prvního vektoru ke druhému, palec ukazuje směr třetího vektoru. Výsledek je stejný.
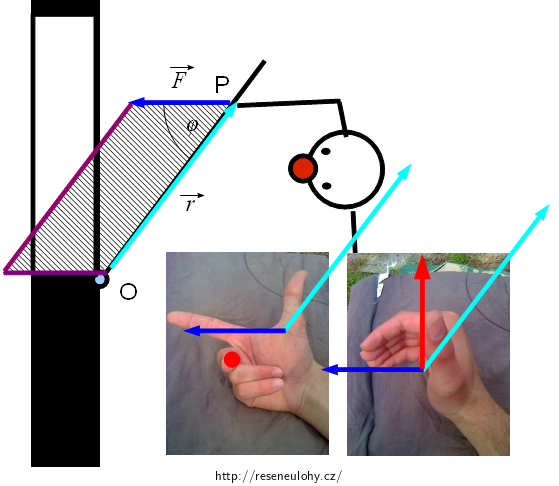
Na obrázku tedy vektor \(\vec M\) míří ke stropu.
(Všimněte si, že na obrázku jsme pro pravidlo pravé ruky vektory posunuli, aby začínaly v jednom bodě. Učinili jsme tak pouze pro lepší názornost, situace se tím nijak nemění.)
Odpověď
Vektor momentu síly \(\vec M\) je rovnoběžný se závěsy okna a míří nahoru.
Jeho velikost je \(rF\sin \varphi\), kde φ je úhel sevřený vektory.
Vektor vychází přímo vzhůru z roviny obrázku, proto je naznačen červenou tečkou (neplést s červeným nosem).




