Intenzita gravitačního pole Země
Úloha číslo: 1245
Určete velikost intenzity \(K\) gravitačního pole Země
Poznámka: Zemi považujte za homogenní kouli.
Rozbor
Nejprve si zopakujte, jak je definovaná intenzita gravitačního pole. Pak řešte dva případy. Vyjádřete si, jak se mění velikost intenzity uvnitř Země, tedy ve vzdálenosti \(r ≤ R\) od středu Země, a vně Země, tedy ve vzdálenosti \(r \gt R\) od středu Země. V prvním případě je třeba ukázat, že ve vzdálenosti \(r ≤ R\) se uplatňuje jen gravitační působení části Země pod slupkou o poloměru \(r\) a gravitační působení od „zbytku“ Země se ruší.
Nápověda 1
Jak je definovaná velikost intenzity gravitačního pole? Pomůže vám podívat se k teorii u úlohy Intenzita gravitačního pole mezi Zemí a Měsícem.
Nápověda 2
Mějme bod A o hmotnosti \(m\) ve vzdálenosti \(r ≤ R\) od středu Země S, viz obrázek (Slupky).
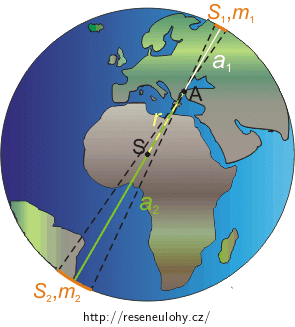
Určete, jak velkou silou \(F_\mathrm{g1}\) působí tenká slupka o hmotnosti \(m_{1}\) na hmotný bod A. \(S_{1}\) značí povrch této slupky. Vzdálenost slupky o hmotnosti \(m_{1}\) od bodu A je \(a_{1}\).
Určete, jak velkou silou \(F_\mathrm{g2}\) působí tenká slupka o hmotnosti \(m_{2}\) na hmotný bod A. \(S_{2}\) značí povrch této slupky. Vzdálenost slupky o hmotnosti \(m_{2}\) od bodu A je \(a_{2}\).
Zjistěte, jaký je vztah mezi \(F_\mathrm{g1}\) a \(F_\mathrm{g2}\).
Poté si nakreslete obdobný obrázek, ale s tím rozdílem, že tentokrát úsečka \(a_{1}\) ani úsečka \(a_{2}\) neprochází středem Země S. Určete velikosti obou sil a vztah mezi nimi i pro tento případ.
Nápověda 3
Máme bod A o hmotnosti \(m\) ve vzdálenosti \(r\) od středu S a platí, že \(r ≤ R\).
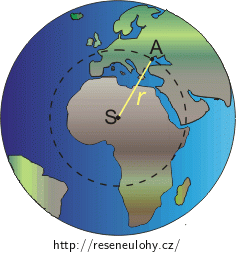
Na hmotný bod A působí gravitační síla, která je vyvolána částí Země o poloměru \(r\).
Pomocí Newtonova gravitačního zákona a vztahu (1) určete velikost intenzity v bodě A.
Nápověda 4
Máme bod A o hmotnosti \(m\) ve vzdálenosti \(r\) od středu Země S a platí, že \(r \gt R\).
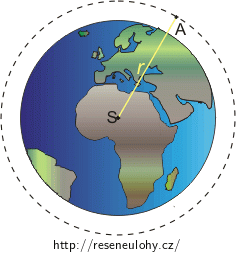
Pomocí Newtonova gravitačního zákona a vztahu (1) určete intenzitu gravitačního pole v bodě A.
Nápověda 5 a)
Jaká je výsledná gravitační síla \(F_\mathrm{g}\), která působí na hmotný bod ve středu Země?
Nápověda 6 b), c), d), e)
Nápověda 7 f)
Zjistili jsme, že pro \(r ≤ R\) platí pro velikost intenzity vztah: \[K=g \frac{r}{R}.\]
Pro \(r \gt R\) platí pro velikost intenzity vztah: \[K=g \frac{R^2}{r^2}.\]
Dále jsme odvodili: \(K\left(0\right)=0\), \(K\left(\frac{R}{2}\right)=\frac{g}{2}\), \(K\left(R\right)=g\) a \(K\left(\frac{3}{2}R\right)=\frac{4}{9}g.\)
(Kde \(g=\kappa \frac{M}{R^2}\).)
S pomocí výše uvedeného sestrojte graf závislosti velikosti intenzity gravitačního pole Země \(K\) na vzdálenosti \(r\) od jejího středu.
Celkové řešení
Velikost intenzity gravitačního pole
Velikost intenzity gravitačního pole \(K\) je definována jako: \[K=\frac{F_\mathrm{g}}{m},\tag{1}\] kde \(F_\mathrm{g}\) je velikost gravitační síly působící v daném místě na hmotný bod o hmotnosti \(m\).
Gravitační působení Země ve vzdálenosti \(r ≤ R\) (kde R je poloměr Země)
Mějme bod A o hmotnosti \(m\) ve vzdálenosti \(r\) od středu S, viz obrázek (Slupky).

Dle Newtonova gravitačního zákona určíme, jakou silou \(F_\mathrm{g1}\) působí slupka o hmotnosti \(m_{1}\) na hmotný bod A: \[F_\mathrm{g1}=\kappa \frac{mm_{1}}{a_{1}^2},\tag{2}\] kde \(a_{1}\) je vzdálenost slupky o hmotnosti \(m_{1}\) od bodu A a \(\kappa\) je gravitační konstanta.
Dle Newtonova gravitačního zákona určíme, jakou silou \(F_\mathrm{g2}\) působí slupka o hmotnosti \(m_{2}\) na hmotný bod A: \[F_\mathrm{g2}=\kappa \frac{mm_{2}}{a_{2}^2},\tag{3}\] kde \(a_{2}\) je vzdálenost slupky o hmotnosti \(m_{2}\) od bodu A.
Zjistíme, jaký je vztah mezi \(F_\mathrm{g1}\) a \(F_\mathrm{g2}\).
Vydělíme vztah (2) vztahem (3): \[\frac{F_\mathrm{g1}}{F_\mathrm{g2}}=\frac{\kappa \frac{mm_{1}}{a_{1}^2}}{\kappa \frac{mm_{2}}{a_{2}^2}}.\] Vykrátíme \(\kappa\) a \(m\): \[\frac{F_\mathrm{g1}}{F_\mathrm{g2}}=\frac{ \frac{m_{1}}{a_{1}^2}}{\frac{m_{2}}{a_{2}^2}}.\] Obě strany rovnice vynásobíme \({F_\mathrm{g2}}\frac{m_{2}}{a_{2}^2}\): \[F_\mathrm{g1}\frac{m_{2}}{a_{2}^2}=F_\mathrm{g2}\frac{m_{1}}{a_{1}^2}.\tag{4}\] Dle definice prostorového úhlu platí: \[\frac{S_{1}}{a_{1}^2}=\frac{S_{2}}{a_{2}^2},\] neboť máme stejné vrcholové úhly.
Obě strany rovnice vynásobíme tloušťkou tenké slupky dr a hustotou Země \(\rho\): \[\frac{S_{1}\mathrm{d}r\rho}{a_{1}^2}=\frac{S_{2}\mathrm{d}r\rho}{a_{2}^2}.\tag{5}\] Platí \(S_{1}\mathrm{d}r\rho=m_{1}\) a \(S_{2}\mathrm{d}r\rho=m_{2}\), po dosazení dostáváme: \[\frac{m_{1}}{a_{1}^2}=\frac{m_{2}}{a_{2}^2}.\tag{6}\] Do vztahu (4) dosadíme za \(\frac{m_{1}}{a_{1}^2}\) dle (6): \[F_\mathrm{g1}\frac{m_{2}}{a_{2}^2}=F_\mathrm{g2}\frac{m_{2}}{a_{2}^2}.\] Obě strany rovnice vydělíme \(\frac{m_{2}}{a_{2}^2}\): \[F_\mathrm{g1}=F_\mathrm{g2}.\]
Podíváme se, jaké budou velikosti obou sil a vztah mezi nimi v případě, že úsečka \(a_{1}\) ani úsečka \(a_{2}\) neprochází středem Země S.
Nakreslíme si obrázek této situace. Vytvoříme kolmé průměty tenkých slupek \(S_{1}\cos{\alpha}\) a \(S_{2}\cos{\alpha}\).
Z obrázku vidíme, že úhly \(\alpha\) jsou stejné. Tedy platí: \[\frac{S_{1}\cos{\alpha}}{a_{1}^2}=\frac{S_{2}\cos{\alpha}}{a_{2}^2}.\] Obě strany rovnice vynásobíme \(\frac{\mathrm{d}r\rho}{\cos{\alpha}}\) a dostáváme vztah: \[\frac{S_{1}\mathrm{d}r\rho}{a_{1}^2}=\frac{S_{2}\mathrm{d}r\rho}{a_{2}^2},\] který odpovídá vztahu (5). Dále výpočet pokračuje jako v předchozím případě a opět dostáváme, že \(F_\mathrm{g1}=F_\mathrm{g2}.\) Síly \(F_\mathrm{g1}\), \(F_\mathrm{g2}\) mají v obou případech stejnou velikost, ale opačný směr. Na hmotný bod ve vzdálenosti \(r < R\) bude tedy působit jen část Země o poloměru r. Gravitační působení „zbytku“ Země se vyruší.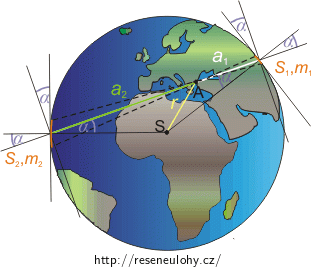
Intenzita působící na hmotný bod uvnitř Země
Máme bod A o hmotnosti \(m\) ve vzdálenosti \(r\) od středu S a platí, že \(r ≤ R\).

Na hmotný bod A působí gravitační síla, která je vyvolána částí Země o poloměru \(r\).
Zformulujeme Newtonův gravitační zákon pro gravitační sílu \(F_\mathrm{g}\), kterou působí část Země o poloměru \(r\) na hmotný bod A: \[F_\mathrm{g}=\kappa \frac{mM_{r}}{r^2},\tag{7}\] kde \(M_{r}\) je hmotnost části Země o poloměru \(r\).
Pro hmotnost \(M_{r}\) bude platit: \[M_{r}= \frac{4}{3} \pi r^3 \rho,\tag{8}\] kde \(\frac{4}{3} \pi r^3\) je objem části Země o poloměru \(r\) a \(\rho\) je hustota Země.
Dosadíme vztah (8) do vztahu (7): \[F_\mathrm{g}=\kappa \frac{m\frac{4}{3} \pi r^3 \rho}{r^2}.\] \(r^2\) vykrátíme a dostáváme: \[F_\mathrm{g}=\kappa m \frac{4}{3} \pi r \rho.\tag{9}\] Dosadíme vztah (9) do vztahu (1): \[K=\frac{\kappa m \frac{4}{3} \pi r \rho}{m}.\] \(m\) vykrátíme a vynásobíme pravou stranu rovnice jedničkou ve tvaru \(\frac{R^3}{R^3}\): \[K=\kappa \frac{4}{3} \pi r \rho\frac{R^3}{R^3}.\] \(\frac{4}{3}\pi R^3 \rho\) odpovídá hmotnosti Země \(M\) a tedy: \[K=\kappa M r \frac{1}{R^3}.\] Dále platí, že gravitační zrychlení \(g=\kappa \frac{M}{R^2}\), po dosazení dostáváme: \[K=g \frac{r}{R},\tag{10}\] kde \(r ≤ R\).
Intenzita působící na hmotný bod vně Země
Máme bod A o hmotnosti \(m\) ve vzdálenosti \(r\) od středu S a platí, že \(r \gt R\).

Pomocí Newtonova gravitačního zákona vyjádříme velikost gravitační síly \(F_\mathrm{g}\), kterou působí Země na hmotný bod A, který se nachází ve vzdálenosti \(r \gt R\): \[F_\mathrm{g}=\kappa \frac{mM}{r^2}.\tag{11}\]
Dosadíme vztah (11) do vztahu (1): \[K=\frac{\kappa \frac{mM}{r^2}}{m}.\] \(m\) vykrátíme a vynásobíme pravou stranu rovnice jedničkou ve tvaru \(\frac{R^2}{R^2}\): \[K= \kappa \frac{M}{r^2}\frac{R^2}{R^2}.\] \(\kappa \frac{M}{R^2}\) odpovídá gravitačnímu zrychlení \(g\) a tedy: \[K=g \frac{R^2}{r^2},\tag{12}\] kde \(r \gt R\).
a) Intenzita ve středu Země
Výsledná gravitační síla \(F_\mathrm{g}\) působící na hmotný bod ve středu Země je nulová, protože všechny síly, kterými působí části Země na bod o hmotnosti \(m\) v jejím středu, se navzájem vyruší. Dosazením za \(F_\mathrm{g}\) do vztahu (1) dostáváme intenzitu ve středu Země \(K\): \[K=\frac{0}{m}=0.\]
Ke stejnému výsledku dojdeme i dosazením za r = 0 do vztahu (10).
Řešení b), c), d) a e)
b) Platí \(\frac{R}{2} \lt R\). Dosadíme \(r=\frac{R}{2}\) do vztahu (10): \[K=g \frac{\frac{R}{2}}{R}.\] \(R\) vykrátíme: \[K=\frac{g}{2}.\]
c) Platí \(R = R\). Dosadíme \(r=R\) do vztahu (10): \[K=g \frac{R}{R}.\] \(R\) vykrátíme: \[K=g.\]
d) Platí \(\frac{R}{2}+R \gt R\). Dosadíme \(r=\frac{3}{2}R\) do vztahu (12): \[K=g \frac{R^2}{\left( \frac{3}{2}R\right)^2}.\] \(R^2\) vykrátíme a upravíme výraz: \[K=\frac{4}{9}g.\]
e) Řešení odpovídá vztahu (12): \[K=g \frac{R^2}{r^2}.\]
Graf závislosti velikosti intenzity gravitačního pole Země \(K\) na vzdálenosti \(r\) od středu Země
Pro \(r ≤ R\) platí vztah: \[K=g \frac{r}{R}.\]
Pro \(r \gt R\) platí vztah: \[K=g \frac{R^2}{r^2}.\]
Dále jsme odvodili: \(K\left(0\right)=0\), \(K\left(\frac{R}{2}\right)=\frac{g}{2}\), \(K\left(R\right)=g\) a \(K\left(\frac{3}{2}R\right)=\frac{4}{9}g.\)
(Kde \(g=\kappa \frac{M}{R^2}\).)
Sestrojíme graf závislosti intenzity gravitačního pole Země \(K\) na vzdálenosti \(r\) od středu Země.
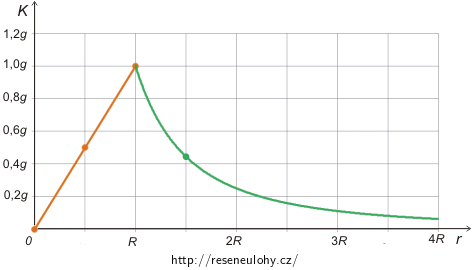
Odpověď
Velikost intenzity \(K\) gravitačního pole Země
a) ve středu Země: \(K\left(0\right)=0\),
b) v hloubce \(\frac{R}{2}\) pod povrchem Země: \(K\left(\frac{R}{2}\right)=\frac{g}{2}\),
c) na povrchu Země: \(K\left(R\right)=g\),
d) ve vzdálenosti \(\frac{R}{2}\) nad Zemí: \(K\left(\frac{3}{2}R\right)=\frac{4}{9}g\),
e) ve vzdálenosti \(r \gt R\): \(K=g \frac{R^2}{r^2}\), (kde \(g=\kappa \frac{M}{R^2}\)).
f) Graf závislosti intenzity gravitačního pole Země na vzdálenosti od středu:



