Sbírka řešených úloh

Otáčení kola

Úloha číslo: 119

• Zápis

  f = 25 Hz	frekvence otáčení kola
  t0 = 30 s	čas, po kterém se kolo zastaví
  ε = ? (s-2)	úhlové zrychlení kola
  N = ?	počet otáček, které kolo vykoná od počátku brzdění do zastavení

• Nápověda 1: Úhlové zrychlení kola

  Uvědomte si, jaký vztah platí mezi okamžitou hodnotou úhlové rychlosti a úhlovým zrychlením kola.

  Jakou počáteční úhlovou rychlostí se kolo pohybovalo před tím, než začalo brzdit? A jaká byla velikost úhlové rychlosti v čase t₀?

• Řešení k nápovědě 1

  Pro okamžitou hodnotu úhlové rychlosti platí vztah:

   

  \[\omega\,=\,\omega_0+\varepsilon{t}\,,\] \[\omega_0\,=\,2\pi f\,=\,50\pi\,\mathrm{s^{-1}}\,.\]

   

  V čase  t = t₀ bude ω = 0, takže:

   

  \[\omega_0+\varepsilon{t_0}\,=\,0\,,\] \[\varepsilon\,=\,-\frac{\omega_0}{t_0}\,=\, -\frac{2\pi f}{t_0}\,=\,-\frac{50}{30}\pi\,\mathrm{s^{-2}}\,=\,-5{,}24\,\mathrm{s^{-2}}\,.\]

• Nápověda 2 : Počet otáček - početní řešení

  Jakým způsobem zjistíte, kolik otáček kolo provedlo za určitý čas?

  Použijte k tomu úhel, který polohový vektor libovolného bodu kola opíše vzhledem ke středu za určitý čas. Ten vyjádříte pomocí velikosti úhlového zrychlení, které znáte z předchozí nápovědy, a velikosti úhlové rychlosti před brzděním kola.

• Řešení k nápovědě 2

  Polohový vektor libovolného bodu kola opíše vzhledem ke středu za čas t₀ úhel:

   

  \[\psi_0\,=\,\omega_0t_0+\frac{\varepsilon{t_0^{2}}}{2}\,=\, 2{\pi}ft_0 + \frac{\varepsilon{t_0^{2}}}{2}\,,\] \[\psi_0\,=\, 1500\pi-\frac{5}{6}\pi900\,=\,750\pi\,.\]

   

  Počet otáček za čas t₀:

   

  \[N\,=\,\frac{\psi_0}{2\pi}\,=\,\frac{750\pi}{2\pi}\,=\,375\,.\]

• Nápověda 3: Počet otáček - grafické řešení

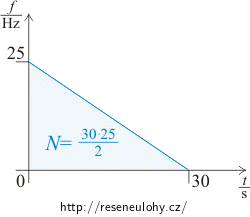
  Počet otáček kola za čas t₀ lze zjistit také graficky.

  Nakreslete graf závislosti frekvence otáčení kola na čase. Kde je v grafu schovaný daný počet otáček?

• Řešení k nápovědě 3

  Grafické řešení:

  

  Počtu otáček odpovídá plocha pod křivkou.

• CELKOVÉ ŘEŠENÍ

  Pro okamžitou hodnotu úhlové rychlosti platí vztah:

   

  \[\omega\,=\,\omega_0+\varepsilon t\,,\] \[\omega_0\,=\,2\pi f\,=\,50\pi\,\mathrm{s^{-1}}\,.\]

   

  V čase t = t₀ bude ω = 0, takže:

   

  \[\omega_0+\varepsilon{t_0}\,=\,0\,,\] \[\varepsilon\,=\,-\frac{\omega_0}{t_0}\,=\,-\frac{2{\pi}f}{t_0} \,=\, -\frac{50}{30}\pi\,\mathrm{s^{-2}}\,=\,-5{,}24\,\mathrm{s^{-2}}\,.\]

   

  Polohový vektor libovolného bodu kola opíše vzhledem ke středu za čas t₀ úhel:

   

  \[\psi_0\,=\,\omega_0t_0+\frac{\varepsilon{t_0^{2}}}{2}\,=\, 2{\pi}ft_0 + \frac{\varepsilon{t_0^{2}}}{2}\,,\] \[\psi_0\,=\, 1500\pi-\frac{5}{6}\pi900\,=\,750\pi\,.\]

   

  Počet otáček za čas t₀:

   

  \[N\,=\,\frac{\psi_0}{2\pi}\,=\,\frac{750\pi}{2\pi}\,=\,375\,.\]

   

  Grafické řešení:

   

  

   

  Počtu otáček odpovídá plocha pod křivkou.

• Odpověď

  Úhlové zrychlení kola ε je:

   

  \[\varepsilon\,=\,-\frac{2{\pi}f}{t_0} \,=\, -5{,}24\,\mathrm{s^{-2}}\,.\]

   

  Počet otáček N, které kolo vykoná od počátku brzdění do zastavení, je:

   

  \[N\,=\,\frac{\psi_0}{2\pi}\,=\,ft_0 + \frac{\varepsilon{t_0^{2}}}{4\pi}\,=\,375\,.\]

• Počet otáček - ještě jinak

  Počet otáček kola lze určit také následujícím způsobem. Frekvence otáčení se s časem mění podle vztahu:

  \[f\left(t\right)\,=\, f_0 - kt\,,\]

  kde

  \[k\,=\,\frac{25}{30}\,\]

  (směrnice přímky v grafu z Nápovědy 3).

  Počet otáček kola od začátku brzdění do zastavení pak můžeme spočítat jako integrál funkce f(t) v daném časovém intervalu (obsah plochy pod křivkou):

  \[N\,=\,\int_{0}^{30}{f(t)}\mathrm{d}t\,=\, \int_{0}^{30}{(f_0 - \frac{25}{30}t)}\mathrm{d}t\,,\] \[N\,=\,\int_{0}^{30}{(f_0 - \frac{5}{6}t)}\mathrm{d}t\,=\, \left[f_0t - \frac{5t^{2}}{6{\cdot}2}\right]_0^{30}\,,\] \[N\,=\, 25{\cdot}30 - \frac{5{\cdot}30^{2}}{2{\cdot}6} \,=\, 375\,.\]

• Podobná úloha

  Zkuste podobnou úlohu Rotor turbíny.