Zahradní hadice
Úloha číslo: 133
Proudem vody tryskajícím ze zahradní hadice počáteční rychlostí o velikosti 15 m·s−1 chceme dostříknout co nejvýše na svislou stěnu, která se nachází ve vodorovné vzdálenosti 10 m od ústí hadice.
a) Jak velký elevační úhel musíme zvolit?
b) Do jaké výšky na stěnu voda dostříkne?
c) Pod jakým úhlem dopadne voda na stěnu? Určete odchylku vektoru okamžité rychlosti v okamžiku dopadu od vodorovného směru.
Odpor vzduchu zanedbejte.
Zápis
v0 = 15 m·s−1 počáteční rychlost proudu vody d = 10 m vzdálenost stěny od ústí hadice α = ? (°) elevační úhel h = ? (m) maximální výška dostřiku vody ψ = ? (°) úhel, pod kterým dopadne voda na stěnu Z tabulek: g = 9,81 m·s−2 tíhové zrychlení Rozbor
Chceme-li zjistit, pod jakým úhlem α musíme namířit hadici, aby voda dostříkla co nejvýše, musíme si nejprve vyjádřit, jak závisí výška dostřiku h na úhlu α. Pak již hledáme maximum funkce h(α).
Pozor na úvahu, že maximální výška dostřiku na zeď bude odpovídat maximální výšce vrhu pro daný úhel α. Uvědomte si, že vzdálenost zdi je pevně daná. Nakreslete si různé možnosti situace.
Nápověda 1 pro a): Obrázek situace, typ pohybu
Nakreslete si obrázek situace. O jaký typ pohybu se jedná? Jak se bude s časem měnit x-ová a y-ová složka rychlosti vody? Jak se bude měnit x-ová a y-ová souřadnice?
Nápověda 2 pro a): Doba doletu vody ke stěně, výška dostřiku
Jak dlouho poletí voda ke stěně pro daný úhel α? Jaká výška h dostřiku na stěnu odpovídá této době?
Nápověda 3 pro a): Elevační úhel α
Potřebujete zjistit, pro jaký úhel α bude výška h dostřiku na stěnu maximální. Hledáte tedy maximum funkce h = h(α). Jak ho zjistíme matematicky?
Nápověda 4 pro b): Maximální výška dostřiku vody
Znáte úhel pro maximální výšku dostřiku a závislost výšky h dostřiku na stěnu na úhlu α. Maximální výšku již snadno dopočítáte.
Nápověda 5 pro c): Úhel ψ dopadu vody na stěnu
Dokreslete si do obrázku vektor rychlosti vody v okamžiku dopadu na stěnu a jeho složky ve směru osy x a y. Příslušný úhel s jejich pomocí snadno vyjádříte. Hodnoty obou složek rychlosti v okamžiku dopadu na stěnu určíte s pomocí vztahu (1) a (2) z Nápovědy 1.
CELKOVÉ ŘEŠENÍ
a) elevační úhel
Obrázek 1:
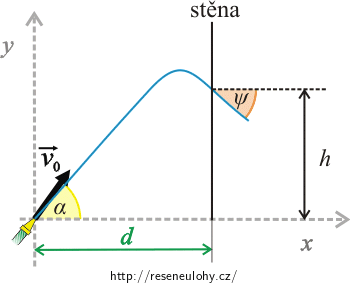
Počátek vztažné soustavy zvolíme v ústí hadice.
Jedná se o šikmý vrh.
X-ová a y-ová složka rychlosti vody a x-ová a y-ová souřadnice se s časem mění následujícím způsobem:
\[v_\mathrm{x}\,=\,v_0\,\cos\alpha,\tag{1}\] \[v_\mathrm{y}\,=\,v_0\,\sin\alpha\,-\,gt,\tag{2}\]
\[x\,=\,v_0t\,\cos\alpha,\tag{3}\] \[y\,=\,v_0t\,\sin\alpha\,-\,\frac{1}{2}gt^{2}.\tag{4}\]Pro dobu letu vody a pro výšku místa dopadu na stěnu platí vztahy: \(x\,=\,d.\)
Pak z (3):
\[d\,=\,v_0t\,\cos\alpha,\] \[t\,=\,\frac{d}{v_0\,\cos\alpha},\tag{5}\]
\[y\,=\,h.\]Pak z (4):
\[h\,=\,v_0t\,\sin\alpha\,-\,\frac{1}{2}gt^{2}.\]Dosadíme za t z (5):
\[h\,=\,d\,\mathrm{tg}\alpha\,-\,\frac{gd^{2}}{2v_0^{2}\,\cos^{2}\alpha}\,=\,d\mathrm{tg}\alpha\,-\,\frac{gd^{2}}{2v_0^{2}}\,\left(1\,+\,\mathrm{tg}^{2}\alpha \right).\tag{6}\]Potřebujeme zjistit, pro jaký úhel α bude výška h dostřiku vody maximální. Jinými slovy hledáme extrém funkce h = h(α).
Zjistíme, kdy je derivace funkce h podle α rovna nule:
\[\frac{\mathrm{d}h}{\mathrm{d}\alpha}\,=\,\frac{\mathrm{d}}{\mathrm{d}\alpha}\left(d\,\mathrm{tg}\alpha\,-\,\frac{gd^{2}}{2v_0^{2}\,\cos^{2}\alpha}\right),\] \[\frac{\mathrm{d}h}{\mathrm{d}\alpha}\,=\,\frac{d}{\cos^{2}\alpha}\,-\,\frac{gd^{2}\sin\alpha}{v_0^{2}\cos^{3}\alpha}\,=\,\frac{d}{\cos^{2}\alpha}\left(1\,-\,\frac{gd}{v_0^{2}}\,\mathrm{tg}\alpha\right)\,=\,0,\] \[1\,-\,\frac{gd}{v_0^{2}}\,\mathrm{tg}\alpha \,=\, 0,\] \[\mathrm{tg}\alpha\,=\,\frac{v_0^{2}}{gd}.\tag{7}\]Pro elevační úhel \[\alpha\,=\,\mathrm{arctg}\,\frac{v_0^{2}}{gd},\] dosáhne tedy funkce h(α) maxima.
Pro zadané hodnoty:
\[\mathrm{tg}\alpha\,=\,\frac{15^{2}}{9{,}81{\cdot}10} \,\dot=\, 2{,}294,\] \[\alpha\,=\,\mathrm{arctg}\,2{,}294\,\,\dot=\,\,66{,}4^{\circ}.\]b) Výška dostřiku
Víme, že pro výšku místa dopadu na stěnu platí podle vztahu (6):
\[h\,=\,d\mathrm{tg}\alpha\,-\,\frac{gd^{2}}{2v_0^{2}\cos^{2}\alpha}\,=\,d\mathrm{tg}\alpha\,-\,\frac{gd^{2}}{2v_0^{2}}\left(1\,+\,\mathrm{tg}^{2}\alpha\right)\,.\tag{6}\]Dále víme, že výška h dostřiku na stěnu bude maximální pro úhel α, pro který platí podle vztahu (7):
\[\mathrm{tg}\alpha\,=\,\frac{v_0^{2}}{gd}\,.\tag{7}\]Dosazením vztahu (7) do vztahu (6) dostaneme:
\[h\,=\,\frac{dv_0^{2}}{gd}\,-\,\frac{gd^{2}}{2v_0^{2}}\left(1\,+\,\frac{v_0^{4}}{g^{2}d^{2}}\right)\,=\,\frac{v_0^{2}}{2g}\,-\,\frac{gd^{2}}{2v_0^{2}}\,.\]Číselně:
\[h\,=\,\left(\frac{15^{2}}{2{\cdot}9{,}81}\,-\,\frac{9{,}81{\cdot}10^{2}}{2{\cdot}15^{2}}\right)\,\mathrm{m},\] \[h\,\dot=\,9{,}29\,\mathrm{m}.\]c) odchylka ψ vektoru rychlosti dopadající vody od vodorovného směru
Do obrázku vyznačíme vektor rychlosti dopadající vody, jeho složky a hledaný úhel.
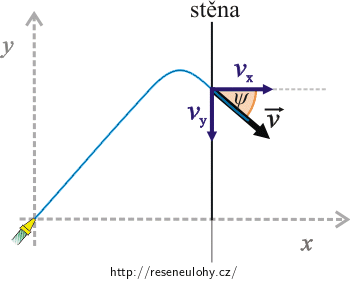
Odchylku ψ rychlosti dopadu od vodorovného směru určíme ze vztahu:
\[\mathrm{tg}\psi\,=\,\frac{v_\mathrm{y}}{v_\mathrm{x}}\,.\]Za vx a vy dosadíme ze vztahů (1) a (2), za čas t pak ze vztahu (5):
\[\mathrm{tg}\psi\,=\,\frac{v_0\,\sin\alpha\,-\,gt}{v_0\cos\alpha}\,=\,\mathrm{tg}\alpha\,-\,\frac{gd}{v_0^{2}\cos^{2}\alpha}\,.\]Upravíme pomocí vztahu (7):
\[\mathrm{tg}\psi\,=\,\mathrm{tg}\alpha\,-\,\frac{1}{\mathrm{tg}\alpha\cos^{2}\alpha},\] \[\mathrm{tg}\psi\,=\,\mathrm{tg}\alpha\,-\,\frac{1}{\sin\alpha\cos\alpha}\,=\,\frac{\sin^{2}\alpha\,-\,1}{\sin\alpha\cos\alpha}\,=\,-\,\frac{1}{tg\alpha}\,=\, -\,\frac{gd}{v_0^{2}}.\]Číselně:
\[\mathrm{tg}\psi\,=\,-\frac{9{,}81{\cdot}10}{15^{2}} \,\dot=\, -0{,}436,\] \[\psi\,\dot=\,-\,23{,}6^{\circ}.\]Odchylka ψ rychlosti dopadu od vodorovného směru vyšla záporná (odčítáme velikost po směru hodinových ručiček). Podívejte se na obrázek.
Poznámka:
Pozor na úvahu, že při maximální výšce dostřiku na stěnu bude y-ová složka rychlosti nulová, a tedy i úhel φ nulový. V úloze je pevně daná vzdálenost stěny, a tím pro daný úhel i doba letu vody.
Odpověď
a) Abychom dostříkli proudem vody co nejvýše na svislou stěnu, musíme zvolit elevační úhel α, pro který platí:
\[\alpha\,=\,\mathrm{arctg}\,\frac{v_0^{2}}{gd}\,\dot=\,66{,}4^{\circ}\,.\]b) Voda dostříkne do výšky h, pro kterou platí:
\[h\,=\,\frac{v_0^{2}}{2g}\,-\,\frac{gd^{2}}{2v_0^{2}}\,\dot=\,9{,}29\,\mathrm{m}\,.\]c) Voda na stěnu dopadne pod úhlem ψ, pro který platí:
\[\mathrm{tg}\psi\,=\,-\,\frac{gd}{v_0^{2}}\,.\]Pro zadané hodnoty:
\[\psi\,=\,-\,23{,}6^{\circ}.\]






