Bruslař
Úloha číslo: 152
Bruslař o hmotnosti 70 kg stojí na bruslích na hladkém ledu. Do pohybu se uvede tím, že ve vodorovném směru odhodí před sebe kouli o hmotnosti 3 kg rychlostí o velikosti 8 m·s-1. Do jaké vzdálenosti bruslař po odhození koule odjede? Součinitel tření mezi ledem a bruslemi je 0,02.
Zápis
M = 70 kg hmotnost bruslaře m = 3 kg hmotnost koule v1 = 8 m·s-1 rychlost odhozené koule f = 0,02 součinitel mezi ledem a bruslemi sz = ? (m) vzdálenost, do které bruslař po odhození koule odjede Rozbor
Nejprve zjistíme, jakou rychlostí se bude pohybovat bruslař po odhození koule. Využijeme k tomu zákon zachování hybnosti (ZZH). Pak nám bude zbývat vyřešit, jaká je dráha zastavení bruslaře, působí-li na něj konstantní brzdná síla. Vyjít můžeme buď ze zákona zachování energie, nebo z Newtonových zákonů.
Nápověda 1 - hybnost soustavy bruslař+koule
Co můžete říct o hybnosti soustavy bruslař+koule před a bezprostředně po odhození koule? Nakreslete si obrázek situace. Jakým směrem se bude pohybovat bruslař a jakým koule?
Nápověda 2 - pohyb bruslaře, práce třecí síly
Jaký pohyb vykonává bruslař, působí-li na něho třecí síla? Jakou práci vykoná třecí síla během brzdění bruslaře? Čemu je tato práce rovna? Co se stane s počáteční kinetickou energií bruslaře?
Číselný výpočet
Dáno:
\[m\,=\,3\,\mathrm{kg},\] \[M\,=\,70\,\mathrm{kg},\] \[v_1\,=\,8\,\mathrm{m \cdot s^{-1}},\] \[f\,=\,0{,}02,\] \[g\,=\,9{,}81\,\mathrm{m \cdot s^{-2}}.\]Hledáme:
\[s_\mathrm{z}\,=\,?,\] \[s_\mathrm{z}\,=\,\frac{m^2v_1^2}{2fM^2g},\] \[s_\mathrm{z}\,=\,\frac{3^2{\cdot}8^2}{2{\cdot}0{,}02{\cdot}70^2{\cdot}9{,}81}\,\mathrm{m},\] \[s_\mathrm{z}\,=\,0{,}3\,\mathrm{m}.\]Odpověď
Bruslař odjede do vzdálenosti \(s_\mathrm{z}\,=\,\frac{m^2v_1^2}{2fM^2g}\,=\,0{,}3\,\mathrm{m}.\)
Celkové řešení
Nejprve zjistíme, jakou rychlostí se bude pohybovat bruslař po odhození koule. Využijeme k tomu zákon zachování hybnosti (ZZH). Pak nám bude zbývat vyřešit, jaká je dráha zastavení bruslaře, působí-lí na něj konstantní brzdná síla. Vyjít můžeme buď ze zákona zachování energie, nebo z Newtonových zákonů.
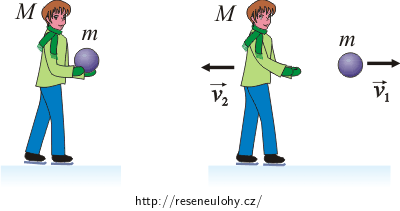
\(m\)…hmotnost koule
\(M\)…hmotnost bruslaře
\(\vec{v_1}\)…vektor rychlosti koule po odhození
\(\vec{v_2}\)…vektor rychlosti bruslaře po odhození koule
Počáteční hybnost soustavy bruslař+koule je nulová, proto podle zákona zachování hybnosti musí být celková hybnost soustavy po odhození předmětu rovněž nulová. Bruslař se bude po odhození koule pohybovat opačným směrem než koule.
Platí:
\[\vec{p_1}+\vec{p_2}\,=\,0,\]\(\vec{p_1}\)…vektor hybnosti koule po odhození,
\(\vec{p_2}\)…vektor hybnosti bruslaře po odhození koule,
\[m\vec{v_1}+M\vec{v_2}\,=\,0.\]Protože vektory rychlostí leži v přímce, můžeme tuto rovnici napsat skalárně:
\[mv_{1}-Mv_{2}\,=\,0.\]Odtud dostaneme velikost rychlosti bruslaře po odhození koule:
\[v_{2}\,=\,\frac{mv_{1}}{M}.\tag{1}\]Na bruslaře působí proti směru jeho pohybu stálá třecí síla:
\[F_\mathrm{t}\,=\,Mgf,\tag{2}\]\(F_\mathrm{t}\)…třecí síla,
\(f\)…koeficient tření,
\(g\)…tíhové zrychlení.
Proto se bruslař pohybuje rovnoměrným zpomaleným pohybem.
Třecí síla vykoná během brzdění na dráze sz práci:
\[W\,=\,F_\mathrm{t}s_\mathrm{z},\]\(W\)…práce třecí síly,
\(s_\mathrm{z}\)…dráha, kterou ujede bruslař do zastavení.
Tato práce je rovna počáteční kinetické energii bruslaře:
\[W\,=\,E_\mathrm{k},\]Ek…počáteční kinetická energie bruslaře.
\[F_\mathrm{t}s_\mathrm{z}\,=\,\frac{1}{2}Mv_2^2,\] \[Mgfs_\mathrm{z}\,=\,\frac{1}{2}Mv_2^2,\] \[s_\mathrm{z}\,=\,\frac{Mv_2^2}{2Mfg}\,=\,\frac{v_2^2}{2fg}.\]Ze vztahu (1) dosadíme rychlost v2:
\[s_\mathrm{z}\,=\,\frac{m^2v_1^2}{2fM^2g},\] \[s_\mathrm{z}\,=\,\frac{3^2{\cdot}8^2}{2{\cdot}0{,}02{\cdot}70^2{\cdot}9{,}81}\,\mathrm{m},\] \[s_\mathrm{z}\,=\,0{,}3\,\mathrm{m}.\]Počáteční kinetická energie bruslaře se během brzdění přemění na vnitřní energii bruslí a ledu, což se projeví jejich zahřátím.
Odpověď: Bruslař odjede do vzdálenosti \(s_\mathrm{z}\,=\,0{,}3\,\mathrm{m}\).
Poznámka:
Dráhu zastavení můžeme zjistit také s využitím 2. Newtonova zákona a kinematických vztahů pro rovnoměrný zpomalený pohyb.
Pohybová rovnice pro bruslaře:
\[\vec{F_\mathrm{t}}+\vec{N}+\vec{F_\mathrm{g}}\,=\,M\vec{a},\]\(\vec{F_\mathrm{t}}\)…třecí síla,
\(\vec{N}\)…síla, kterou působí led na bruslaře,
\(\vec{F_\mathrm{g}}\)…tíhová síla,
\(M\)…hmotnost bruslaře,
\(\vec{a}\)…zrychlení bruslaře.
Skalárně:
\[-F_\mathrm{t}\,=\,Ma,\] \[N-F_\mathrm{g}\,=\,0.\]Vyjádříme si zrychlení bruslaře a:
\[a\,=\,\frac{-F_\mathrm{t}}{M}\,=\,-gf.\]Integrací zrychlení bruslaře dostaneme závislost rychlosti bruslaře na čase po odhození koule:
\[v\,=\,\int{a\mathrm{d}t}\,=\, -gft + K.\tag{3}\] Konstantu K zjistíme z počátečních podmínek. V čase t = 0 s měl bruslař rychlost v = v2, a tedy: \[v_2 \,=\, 0 + K,\] \[v \,=\, v_2-gft.\]Integrací rychlosti bruslaře získáme závislost dráhy bruslaře na čase:
\[s\,=\,\int{v\mathrm{d}t}\,=\,\int{(v_2-gft)\mathrm{d}t}\,=\,v_2t-\frac{1}{2}gft^2+C.\]Konstantu C zjistíme z počátečních podmínek. V čase t = 0 s byla uražená dráha s = 0 m, a tedy:
\[0\,=\,0+C,\] \[s\,=\,v_2t-\frac{1}{2}gft^2.\]V okamžiku zastavení tz je v = 0:
\[0\,=\,v_2-gft_\mathrm{z}.\]Odsud si vyjádříme čas zastavení tz:
\[t_\mathrm{z}\,=\,\frac{v_2}{gf}.\]Dráhu zastavení dostaneme dosazením času zastavení do vztahu pro dráhu s:
\[s_\mathrm{z}\,=\,v_2t_\mathrm{z}-\frac{1}{2}gft_\mathrm{z}^2,\] \[s_\mathrm{z}\,=\,\frac{v_2^2}{gf}-\frac{v_2^2}{2gf},\] \[s_\mathrm{z}\,=\,\frac{v_2^2}{2fg}.\]






