Kmitání pružiny (pružinového oscilátoru)

Úloha číslo: 4501

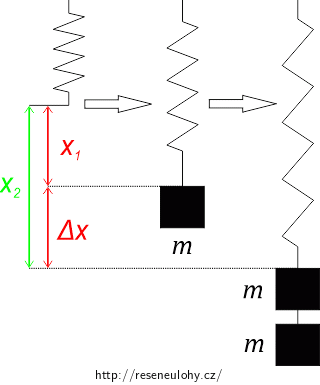
a)	Závaží o hmotnosti 0,10 kg visí na pružině s koeficientem tuhosti 50 N·m^-1, která je upnutá na horním konci. Na pružinu zavěsíme další stejné závaží. Vypočítejte, o kolik se pružina prodlouží v důsledku přidání druhého závaží.
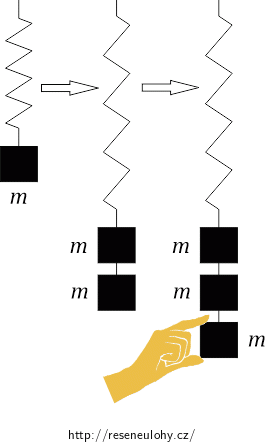
b)	Na pružinu zavěsíme třetí stejné závaží, držíme ale závaží tak, aby se pružina dál nenatahovala. Potom závaží pustíme a ta začnou kmitat ve svislém směru. Poloha, ze které jsme závaží spouštěli, je horní krajní poloha. Vypočítejte celkové prodloužení pružiny (se 3 závažími), když je oscilátor v rovnovážné poloze.
c)	Určete amplitudu kmitání a vypočítejte dobu kmitu (periodu).
d)	Vypočítejte maximální rychlost kmitání a maximální zrychlení kmitání oscilátoru.
e)	Vypočítejte maximální kinetickou energii kmitajícího systému závaží.
f)	Ve chvíli, kdy jsou závaží v nejnižší poloze, se jedno ze závaží odlomí a na pružině zůstanou jen dvě závaží. Zapište novou amplitudu kmitání oscilátoru se dvěmi závažími.
g)	Vypočítejte maximální potenciální energii pružnosti tohoto kmitajícho systému.

Zápis

m = 0,10 kg	hmotnost jednoho závaží
k = 50 N·m^-1	tuhost pružiny

a) x₁ = ?	prodloužení po 1. závaží
x₂ = ?	prodloužení po 2. závaží
\(\Delta x\) = ?	změna prodloužení po 2. závaží
b) x₃ = ?	prodloužení po 3. závaží
c) x_max = ?	amplituda kmitů
T = ?	perioda kmitů
d) v_max = ?	maximální rychlost kmitání
a_max = ?	maximální zrychlení kmitání
e) E_{k_max} = ?	maximální kinetická energie systému
f) x_max2 = ?	nová amplituda kmitání oscilátoru
g) E_{p_max} = ?	maximální potenciální energie systému

g = 9,81 m·s^-2

tíhové zrychlení

Nápověda a) Prodloužení po 2. závaží
Určete nejprve, o kolik se prodlouží pružina při zavěšení jednoho závaží. Jaké síly na závaží působí? Jaká je jejich výslednice v rovnovážné poloze?

Obdobně postupujte při výpočtu prodloužení při zavěšení 2. závaží.
Řešení nápovědy a) Prodloužení pružiny
V rovnovážné poloze působí na pružinu síla pružnosti F = kx₁ a tíhová síla F_G = mg v opačném směru, jejich výslednice musí být nulová.

Po zavěšení prvního závaží se pružina prodlouží o
\[F = kx_1 = mg \rightarrow x_1 = \frac{mg}{k}.\]
Po zavěšení druhého závaží se pružina prodlouží o
\[F = kx_2 = k(x_1 + \Delta x) = 2mg \rightarrow k\Delta x = 2mg - kx_1 = 2mg - mg = mg \] \[\Delta x = \frac{mg}{k} = \frac{0{,}1 \ \text{kg} \cdot 9{,}81 \ \text{m}\cdot \text{s}^{-2}}{50 \ \text{N}\cdot \text{m}^{-1}} = 0{,}01962 \ \text{m} \,\dot=\, 1{,}96 \ \text{cm}\]
Všimněte si, že toto prodloužení 1,96 cm po zavěšení 2. závaží je stejné, jako kdybychom zavěsili 1 závaží na pružinu bez závaží. Celkové prodloužení bude x₂ = 3,92 cm.
Nápověda b) Třetí závaží
O kolik se pružina prodloužila po zavěsení 1. závaží? O kolik po 2. závaží? O kolik se prodlouží po zavěsení 3. závaží?
Řešení nápovědy b) Třetí závaží
Po zavěšení 1 závaží se pružina prodloužila o 1,962 cm. Po zavěšení 2. se prodloužila o dalších 1,962 cm (tedy celkové prodloužení z původní polohy je x₂ = 2·1,962 cm). Po zavěšení 3. závaží bude celkové prodloužení pružiny v rovnovážné poloze x₃ = 3·1,962 cm = 5,886 cm \(\dot{=}\) 5,89 cm .
Nápověda c) Amplituda kmitání - 3 závaží
Amplituda je maximální výchylka kmitavého pohybu. Vůči čemu tuto výchylku měříme? Připomeňte si vztah, pomocí kterého můžeme vypočítat periodu kmitání.

Uvědomte si, že známe prodloužení pružiny v horní krajní poloze oscilátoru i v jeho rovnovážné poloze.
Řešení nápovědy c) Amplituda kmitání - 3 závaží
Známe protažení pružiny v rovnovážné poloze při 3 zavěšených závažích. Víme také, že horní krajní poloha oscilátoru odpovídá rovnovážné poloze při zavěšení 2 závaží. Amplituda kmitání je daná rozdílem těchto dvou protažení, tedy x_max = x₃ - x₂ \(\dot{=}\) 1,96 cm.

Perioda kmitání je
\[T = 2\pi \sqrt{\frac{3m}{k}} = 2\pi \sqrt{\frac{0{,}3 \ \text{kg}}{50 \ \text{N}\cdot \text{m}^{-1}}} = 0{,}4867 \ \text{s} \,\dot = \,0{,}49\ \text{s}.\]
Nápověda d) Max rychlost a zrychlení
Rozmyslete si, jak se během kmitání mění rychlost závaží, ve které poloze bude nejmenší a kde největší? Jak to bude se zrychlením? Připoměňte nebo najděte si vztahy pro závislost rychlosti a zrychlení oscilátoru na čase. Pro jakou hodnotu sin a cos bude rychlost a zrychlení maximální?
Řešení nápovědy d) Max rychlost a zrychlení
Pro závislost výchylky, rychlosti a zrychlení na čase platí následující vztahy:
\[x = x_{\text{max}} \cos(\omega t)\] \[v = -\omega x_{\text{max}} \sin(\omega t)\] \[a = -\omega^2 x_{\text{max}} \cos(\omega t)\]
Hodnoty jsou maximální právě tehdy, když sin, respektive cos nabývají hodnoty 1.

Velikost maximální rychlosti kmitání tedy vypočítáme jako
\[v_{max} = \omega x_{max} = \frac{2\pi}{T}x_{max} = \frac{2\pi}{0{,}4867 \ \text{s}}\cdot 0{,}01962 \ \text{m} = 0{,}253 \ \text{m}\cdot \text{s}^{-1} \,\dot= \,0{,}25 \ \text{m}\cdot \text{s}^{-1} .\]
Velikost maximálního zrychlení kmitání bude
\[a_{max} = \omega^2x_{max} = \left(\frac{2\pi}{0{,}4867 \ \text{s}}\right)^2\cdot \ 0{,}01962 \ \text{s} \,\dot =\, 3{,}27 \ \text{m}\cdot \text{s}^{-2}.\]
Znaménka u vztahů pro rychlost a zrychlení nás nezajímají, chceme zjistit velikost těchto hodnot.
Nápověda e) Max kinetická energie
Připoměňte si vztah pro kinetickou energii. Ve které poloze oscilátoru bude kinetická energie maximální?
Řešení nápovědy e) Max kinetická energie
Kinetická energie je maximální, když je rychlost maximální, tedy při průchodu rovnovážnou polohou. Dosazením do vzorce pro kinetickou energii tedy dostaneme:
\[E_{k} = \frac{1}{2}mv^2 \rightarrow E_{k_{max}} = \frac{1}{2}(3m)v_{max}^ 2 = \frac{1}{2}\cdot 0{,}3 \ \text{kg} \cdot (0{,}253 \ \text{m}\cdot \text{s}^{-1})^2 \, \dot=\, 0{,}0096 \ \text{J} = 9{,}6 \ \text{mJ}.\]
Nápověda f) Odlomení závaží
Kde bude po odlomení rovnovážná poloha, jaké je prodloužení pružiny v této poloze? Jaká je krajní poloha kmitání, jaké je prodloužení pružiny v této krajní poloze? Dokážete z těchto informací určit amplitudu?
Řešení nápovědy f) Odlomení závaží
Po odlomení 3. závaží bude rovnovážná poloha \(kx_2 = 2mg \rightarrow x_2 = \frac{2mg}{k}\).

V předchozí části, kdy kmitaly 3 závaží, jsme vypočítali amplitudu kmitů jako \(x_{max} = \frac{mg}{k} \,\dot=\, 1{,}96 \ \text{cm}\). Pro rovnovážnou polohu platilo \( kx_3 = 3mg \rightarrow x_3 = \frac{3mg}{k} \, \dot= \,5{,}89 \ \text{cm}.\)

Prodloužení v dolní krajní poloze tedy bude \(x_3 + x_{max} = \frac{3mg}{k} + \frac{mg}{k} = \frac{4mg}{k}.\)

Jelikož amplituda je rozdíl prodloužení v krajní poloze a rovnovážné poloze, tak musí platit:
\[x_{max2}= \frac{4mg}{k} - \frac{2mg}{k} = \frac{2mg}{k} = \frac{0{,}2 \ \text{kg} \cdot 9{,}81 \ \text{m}\cdot \text{s}^{-2}}{50 \ \text{N}\cdot \text{m}^{-1}} = 0{,}03924 \ \text{m} \, \dot= \,3{,}92 \ \text{cm.}\]
Nápověda g) Max potenciální energie
Jaký je vztah pro potenciální energii pružnosti? Jaká veličina musí být maximální, aby byla potenciální energie maximální?
Řešení nápovědy g) Max potenciální energie
Potenciální energie pružnosti roste se čtvercem výchylky, její maximum tedy bude v krajních polohách.
\[E_p = \frac{1}{2}kx^2 \rightarrow E_{p_{max}} = \frac{1}{2}kx_{max2}^2 = \frac{1}{2}\cdot 50 \ \text{N}\cdot \text{m}^{-1} \cdot (0{,}03924)^2 \ \text{m} \, \dot=\, 0{,}0385 \ \text{J} = 38{,}5 \ \text{mJ.}\]

Odpovědi

a)	Po zavěšení druhého závaží se pružina prodlouží o \(\Delta x \) \(\dot{=}\) 1,96 cm
c)	Celkové prodloužení pružiny se 3 závažími v rovnovážné poloze je x₃ \(\dot{=}\) 5,89 cm
c)	Amplituda kmitání bude x_max \(\dot{=}\) 1,96 cm, perioda T \(\dot{=}\) 0,49 s
d)	Maximální rychlost kmitání je v_max \(\dot{=}\) 0,25 m·s^-1, maximální zrychlení a_max \(\dot{=}\) 3,27 m·s^-2
e)	Maximální kinetická energie systému závaží bude E_{k_max} \(\dot{=}\) 9,6 mJ
f)	Nová amplituda kmitání se dvěmi závažími bude x_max2 \(\dot{=}\) 3,92 cm
g)	Maximální potenciální energie systému je E_{p_max} \(\dot{=}\) 38,5 J