Balistické kyvadlo I
Úloha číslo: 146
Střela o hmotnosti m zasáhne balistické kyvadlo délky L, hmotnosti M a uvízne v něm. Kyvadlo se vychýlí o úhel α z rovnovážné polohy. Určete velikost rychlosti střely.
Poznámka: Balistické kyvadlo se dříve užívalo k měření rychlosti střel. Může ho tvořit např. dřevěný hranol zavěšený na dvou dlouhých závěsech tak, aby se kýval jen ve svislé rovině.
Zápis
m hmotnost střely L délka kyvadla M hmotnost kyvadla α úhel vychýlení kyvadla v1 = ? rychlost střely před srážkou Nápověda 1 - vychýlení kyvadla
Do jaké výšky se vychýlí kyvadlo po zasažení střelou? Nakreslete si obrázek.
Nápověda 2 - hybnost
Protože střela v kyvadle po srážce zůstane, můžeme říct, že se jedná o dokonale nepružnou srážku. Co můžete říct o hybnosti před a po srážce?
Nápověda 3 - energie
Při nepružné srážce se část mechanické energie střely přemění na vnitřní energii střely a kyvadla. Zákon zachování mechanické energie tedy nemůžeme použít při srovnání situace před srážkou (1) a po srážce (2). Po zavrtání střely se již mechanická energie zachovává, neuvažujeme-li odpor prostředí. Porovnejte ji v situaci těsně po zavrtání střely (2) a při maximální výchylce kyvadla (3).
Celkové řešení
Nejprve vyjádříme výšku, do které vystoupí kyvadlo.
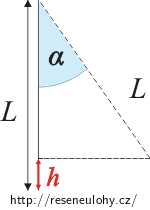
\(L\)…délka kyvadla
\(\alpha\)…úhel vychýlení kyvadla
\(h\)…výška, do které kyvadlo vystoupí
Výšku h, do které kyvadlo vystoupí, vyjádříme pomocí délky kyvadla a úhlu vychýlení:
\[h\,=\,L-L\cos \alpha\,=\,L\left(1-\cos \alpha\right).\tag{1}\]Při řešení dále využijeme zákon zachování hybnosti a energie.
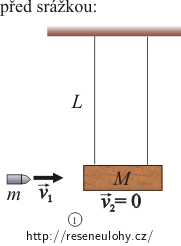
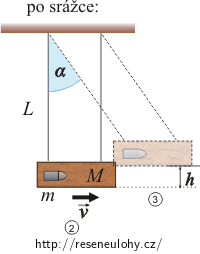
\(m\)…hmotnost střely
\(M\)…hmotnost kyvadla
\(v_1\)…rychlost střely před srážkou
\(v_2\)…rychlost kyvadla před srážkou
\(v\)…rychlost soustavy kyvadlo+střela těsně po srážce
Při dokonale nepružné srážce platí zákon zachování hybnosti (ZZH):
Součet hybností těles v izolované soustavě je konstantní neboli celková hybnost izolované soustavy se zachovává:
\[\vec{p_1}+\vec{p_2}\,=\,\vec{p},\]\(\vec{p_1}\)…vektor hybnosti střely před srážkou,
\(\vec{p_2}\)…vektor hybnosti kyvadla před srážkou,
\(\vec{p}\)…vektor hybnosti soustavy střela+kyvadlo po srážce,
\[m\vec{v_1}+M\vec{v_2}\,=\,\left(m+M\right)\vec{v}.\]Na počátku bylo kyvadlo v klidu, \(v_2 \,=\, 0\):
\[m\vec{v_1}\,=\,\left(m+M\right)\vec{v}.\]Vektory \(\vec{v_1}\) a \(\vec{v}\) leží v přímce, rovnici můžeme přepsat skalárně:
\[mv_1\,=\,\left(m+M\right)v,\] \[v\,=\,\frac{mv_1}{m+M}.\tag{2}\]Při nepružné srážce se část mechanické energie střely přemění na vnitřní energii střely a kyvadla. Zákon zachování mechanické energie tedy nemůžeme použít při srovnání situace před srážkou (1) a po srážce (2). Po zavrtání střely se již mechanická energie zachovává, neuvažujeme-li odpor prostředí.
Zákon zachování mechanické energie (ZZME):
Celková mechanická energie izolované soustavy se zachovává neboli součet potenciální a kinetické energie je konstantní.
Hladinu nulové potenciální energie volíme v situaci 2.
\[E_\mathrm{k}\,=\,E_\mathrm{p}\]\(E_\mathrm{k}\)…kinetická energie soustavy střela+kyvadlo těsně po srážce
\(E_\mathrm{p}\)…potenciální energie soustavy střela+kyvadlo po vychýlení
\[\frac{1}{2}\left(m+M\right)v^2\,=\,\left(m+M\right)gh\tag{3}\]Za rychlost v dosadíme ze vztahu (2):
\[\frac{1}{2}\left(m+M\right)\frac{m^2v_1^2}{\left(m+M\right)^2}\,=\,\left(m+M\right)gh.\]Vyjádříme hledanou rychlost střely na počátku v1:
\[v_1\,=\,\sqrt {2gh}\left(1+\frac{M}{m}\right).\]Za výšku h dosadíme ze vztahu (1):
\[v_1\,=\,\sqrt {2gL\left(1-\cos \alpha \right)}\left(1+\frac{M}{m}\right).\]Odpověď: Rychlost střely před srážkou je \[v_1\,=\,\sqrt {2gL\left(1-\cos \alpha\right)}\left(1+\frac {M}{m}\right).\]
Poznámka:
Zákon zachování energie pro situaci před srážkou a po srážce by vypadal takto:
\[E_\mathrm{ks}\,=\,E_\mathrm{k}+\Delta U,\]\(E_\mathrm{ks}\)…kinetická energie střely před srážkou,
\(E_\mathrm{k}\)…kinetická energie soustavy střela+kyvadlo těsně po srážce,
\(\Delta U\)…změna vnitřní energie,
\[\frac{1}{2}mv_1^2\,=\,\frac{1}{2}\left(m+M\right)v^2+\Delta U.\]Odpověď
Rychlost střely před srážkou je \[v_1\,=\,\sqrt {2gL\left(1-\cos \alpha\right)}\left(1+\frac {M}{m}\right).\]





