Řetízkový kolotoč
Úloha číslo: 203
Řetízkový kolotoč o poloměru 5 m se otáčí úhlovou rychlostí 1 rad·s−1. Náhle se utrhne prázdná sedačka o hmotnosti 1,5 kg a padá z výšky 3 m.
Kterým směrem a jak daleko dopadne?
Zápis
r = 5 m poloměr kolotoče ω = 1 rad·s−1 úhlová rychlost otáčení kolotoče m = 1,5 kg hmotnost sedačky h = 3 m výška, ze které sedačka padá d = ? (m) vzdálenost, do které sedačka dopadne Z tabulek: g = 9,81 m·s−2 tíhové zrychlení Nápověda 1
Jaký pohyb vykonává sedačka před utržením? Jaký je v každém okamžiku směr její rychlosti? Jaké na ni působí síly? Řešte z pohledu inerciálního pozorovatele spojeného se zemí.
Nápověda 2
Jak se změní silové působení v okamžiku utržení sedačky? Jakým směrem sedačka „odletí“?
Nápověda 3
Sedačka se bezprostředně po utržení pohybuje ve směru tečny k původně opisované kružnici a její další pohyb ovlivňuje pouze tíhová síla. Jde tedy o složení rovnoměrného přímočarého pohybu a volného pádu. Jaký druh pohybu v tomto popisu poznáváte?
Nápověda 4
Jak je poloha tělesa při tomto pohybu popsána v závislosti na čase? Vyjádřete průběh x-ové a y-ové souřadnice.
Nápověda 5
Jakou velikost má počáteční rychlost v0? Má nějaký vztah k rychlosti, se kterou se sedačka pohybovala po kružnici před utržením?
Nápověda 6
Nalézt vzdálenost, do které sedačka dopadne, znamená spočítat délku d vodorovného vrhu. Jakou velikost bude mít x-ová a y-ová souřadnice na konci vrhu v čase tk? Dosaďte do rovnic (1a) a (1b) a vyjádřete délku vrhu d.
Celkové řešení
Protože kolotoč se otáčí se stálou úhlovou frekvencí ω, vykonává sedačka rovnoměrný pohyb po kružnici ve vodorovné rovině. Pro takový pohyb platí, že vektor rychlosti sedačky má v každém okamžiku v každém bodě směr tečny k opisované kružnici.
Při tomto pohybu působí na sedačku z pohledu inerciálního pozorovatele spojeného se zemí dvě síly (viz obrázek):
- tíhová síla Země \(\vec{F}_\mathrm{G},\)
- tahová síla závěsu \(\vec{F}_\mathrm{z}.\)
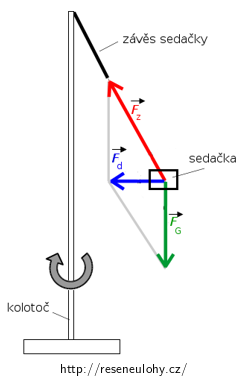
Výslednicí těchto sil je síla dostředivá síla \(\vec{F}_\mathrm{d}\,=\,\vec{F}_\mathrm{G}\,+\,\vec{F}_\mathrm{z}\), která zakřivuje trajektorii sedačky ve vodorovné rovině a je příčinou pohybu po kružnici.
Když se sedačka utrhne, náhle zmizí síla závěsu \(\vec{F}_\mathrm{z}\) a s ní také síla dostředivá. Tato síla pohyb sedačky ve vodorovné rovině zakřivovala, takže po jejím vymizení se sedačka bude pohybovat dále ve směru, který měla její rychlost v okamžiku utržení. Sedačka tedy odletí ve směru tečny k původně opisované kružnici v bodě, kde se utrhla.
Jedinou silou, která bude na sedačku dále působit, je tíhová síla Země. Pohyb se tedy bude dále skládat z rovnoměrného přímočarého pohybu a volného pádu. Takovému pohybu říkáme vodorovný vrh, zde s počáteční výškou h a nějakou počáteční rychlostí v0. Tento vodorovný vrh je popsán vztahy:
\[x(t)\,=\,v_0t,\tag{1a}\]
\[y(t)\,=\,h-\frac{1}{2}gt^2,\tag{1b}\]
kde g je tíhové zrychlení.
(Tyto rovnice odpovídají volbě počátku soustavy souřadnic v bodě ležícím na zemi svisle pod místem, kde se sedačka utrhla.)
Počáteční rychlost v0 vodorovného vrhu je rovna rychlosti, kterou měla sedačka v okamžiku, kdy se utrhnula. Jde tedy o rychlost, se kterou se sedačka pohybovala rovnoměrným pohybem po kružnici. Této rychlosti říkáme obvodová rychlost a platí pro ni vztah:
\[v_0\,=\,\omega r,\tag{2}\]
kde ω je úhlová rychlost a r je poloměr opisované kružnice.
Po uplynutí doby vodorovného vrhu tk dopadne sedačka na zem (takže její y-ová souřadnice bude nulová) do vzdálenosti d (takže její x-ová souřadnice bude rovna d). S použitím této znalosti a dosazením z rovnice (2) do rovnic (1a) a (1b) dostáváme pro souřadnice:
\[x(t_\mathrm{k})\,=\,d\,=\,\omega rt_\mathrm{k},\] \[y(t_\mathrm{k})\,=\,0\,=\,h-\frac{1}{2}gt_\mathrm{k}^2.\]Z druhé rovnice vyjádříme tk:
\[t_\mathrm{k}\,=\,\sqrt{\frac{2h}{g}}.\]Délka vrhu (a tedy vzdálenost, do které sedačka odletí) je z první rovnice dána vztahem:
\[d\,=\,\omega rt_\mathrm{k}\,=\,\omega r\sqrt{\frac{2h}{g}}.\] Po dosazení číselných hodnot: \[d\,=\,\omega r\sqrt{\frac{2h}{g}}\,=\,(1{\cdot}5\cdot\sqrt{\frac{2{\cdot}3}{9{,}81}})\,\mathrm{m}\,\dot{=}\,3{,}9\,\mathrm{m}.\]Je zajímavé si povšimnout, že tato vzdálenost nezáleží na hmotnosti sedačky.
Výsledek
Sedačka odletí ve směru tečny ke kružnici v místě, kde se utrhla. Dopadne ve vzdálenosti: \(d\,=\,\omega r \sqrt{\frac{2h}{g}}\,\dot{=}\,3{,}9\,\mathrm{m}\).






