Anička na výletě
Úloha číslo: 17
Anička si vyjela na kole na výlet. Nejprve stoupala do kopce přibližně konstantní rychlostí o velikosti 10 km·h−1 –. Tak ujela šestinu celkové trasy. Na dalším úseku rovném jedné třetině celkové trasy už měla před sebou rovnou silnici, ale protože projížděla nádhernou krajinou, kterou si chtěla prohlédnout, zrychlila jen mírně a pohybovala se konstantní rychlostí o velikosti 20 km·h−1. Zbývající část své trasy už pospíchala do cíle, proto ujížděla zhruba konstantní rychlostí o velikosti 30 km·h−1.
a) Jak velká byla její průměrná rychlost na celé trase?
b) Jak velká by byla průměrná rychlost Aničky v případě, kdyby se šestinu celkové doby pohybu pohybovala rychlostí velikosti 10 km·h−1, třetinu celkové doby rychlostí velikosti 20 km·h−1 a zbytek rychlostí velikosti 30 km·h−1?
Poznámka: Průměrnou rychlost užíváme ve smyslu průměrné velikosti rychlosti.
Zápis
v1 = 10 km·h−1 rychlost Aničky na prvním úseku v2 = 20 km·h−1 rychlost Aničky na druhém úseku v3 = 30 km·h−1 rychlost Aničky na třetím úseku vp = ? (km·h−1) průměrná rychlost Aničky Nápověda 1 pro a): Průměrná rychlost na celé trase
Vyjádřete si, za jaké časy Anička urazila jednotlivé úseky cesty. Jaký byl celkový čas, za který ujela celou dráhu? Jak s pomocí celkové dráhy a celkového času určíte průměrnou rychlost?
Nápověda 2 pro b): Průměrná rychlost v případě b)
Vyjádřete si opět délky jednotlivých úseků pomocí rychlosti a času. Pak vyjádřete celkovou dráhu, kterou Anička ujela. Průměrnou rychlost pak už snadno určíte jako v předchozí části.
CELKOVÉ ŘEŠENÍ
Průměrnou rychlost bereme jako celkovou uraženou dráhu za celkovou dobu pohybu.
ad a)
Celkovou dráhu označíme s, jednotlivé úseky pak s1, s2, s3.
Platí, že:
\[s_1\,=\,\frac{s}{6} \,,\hspace{30px} s_2\,=\,\frac{s}{3} \,,\hspace{30px} s_3\,=\,\frac{s}{2}\,.\]Dále platí, že:
\[s_1\,=\,v_1t_1 \,,\hspace{30px} s_2\,=\,v_2t_2 \,,\hspace{30px} s_3\,=\,v_3t_3\,.\]Odtud:
\[t_1 \,=\, \frac{s_1}{v_1} \,=\, \frac{s}{6v_1} \,,\hspace{30px} t_2\,=\,\frac{s_2}{v_2} \,=\, \frac{s}{3v_2} \,,\hspace{30px} t_3\,=\,\frac{s_3}{v_3} \,=\, \frac{s}{2v_3}\,.\]Průměrnou rychlost určíme jako celkovou uraženou dráhu za celkovou dobu pohybu:
\[v_\mathrm{p}\,=\,\frac{s}{t_1+t_2+t_3}\,=\,\frac{s}{\frac{s}{6v_1}+\frac{s}{3v_2}+\frac{s}{2v_3}}\,=\,\frac{6v_1v_2v_3}{3v_1v_2+2v_1v_3+v_2v_3}\,.\]Číselně:
\[v_\mathrm{p}\,=\,\frac{(6{\cdot} 10\cdot 20{\cdot} 30)\,\mathrm{km}}{(3{\cdot} 10\cdot 20+2{\cdot} 10\cdot 30+20{\cdot} 30)\,\mathrm{h}}\,=\,20\,\mathrm{km\cdot h^{-1}}\,.\]Poznámka:
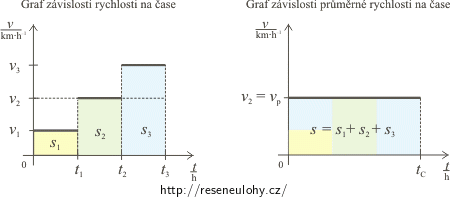
Úlohu můžeme řešit i graficky. Nakreslíme graf závislosti rychlosti na čase (t1 = t2 = t3) a graf závislosti průměrné rychlosti na čase.
Plocha pod křivkami v obou grafech má význam celkové uražené dráhy a musí být stejná. Z grafů je zřejmé, že vp = v2.
ad b)
Označíme si s1, s2, s3 délky úseků dráhy projeté rychlostmi o velikostech v1, v2, v3 za časy t1, t2, t3 a tc celkovou dobu pohybu.
Podle zadání platí:
\[t_1\,=\,\frac{t_\mathrm{c}}{6}\,,\hspace{30px}t_2\,=\,\frac{t_\mathrm{c}}{3}\,,\hspace{30px}t_3\,=\,\frac{t_\mathrm{c}}{2}\,.\]Pro úseky dráhy pak platí:
\[s_1\,=\,\frac{v_1t_\mathrm{c}}{6}\,,\hspace{30px}s_2\,=\,\frac{v_2t_\mathrm{c}}{3}\,,\hspace{30px}s_3\,=\,\frac{v_3t_\mathrm{c}}{2}\,.\]Průměrnou rychlost vp vypočteme následovně:
\[v_\mathrm{p}\,=\,\frac{s_1+s_2+s_3}{t_\mathrm{c}}\,=\,\frac{\frac{v_1t_\mathrm{c}}{6}+\frac{v_2t_\mathrm{c}}{3}+\frac{v_3t_c}{2}}{t_\mathrm{c}}\,=\,\frac{v_1+2v_2+3v_3}{6}\,.\]Číselně:
\[v_\mathrm{p}\,=\,\frac{(10+2{\cdot} 20+3{\cdot} 30)}{6}\,\mathrm{km\cdot h^{-1}}\dot=23{,}3\,\mathrm{km\cdot h^{-1}}\,.\]Odpověď
a) Průměrná rychlost Aničky na celé trase je:
\[v_\mathrm{p}=\frac{6v_1v_2v_3}{3v_1v_2+2v_1v_3+v_2v_3}\,.\]Číselně:
\[v_\mathrm{p}\,=\,20\,\mathrm{km\cdot h^{-1}}\,.\]b) Průměrná rychlost Aničky v případě, že se šestinu celkové doby pohybu pohybovala rychlostí velikosti v1, třetinu celkové doby rychlostí velikosti v2 a zbytek rychlostí velikosti v3, je:
\[v_\mathrm{p} = \frac{v_1+2v_2+3v_3}{6}\,.\]Číselně:
\[v_\mathrm{p}\,\dot=\,23{,}3\,\mathrm{km\cdot h^{-1}}\,.\]