Balistické kyvadlo 2
Úloha číslo: 147
Střela o hmotnosti 4 g vletí do balistického kyvadla vodorovně rychlostí o velikosti 600 m·s-1. Kyvadlo má hmotnost 1 kg a tloušťku 25 cm. Střela jím proletí a vystoupí rychlostí o velikosti 100 m·s-1. Vypočítejte velikost konstantní síly, která střelu v kyvadle brzdí, a výšku, do které se kyvadlo vychýlí.
Poznámka: Balistické kyvadlo se dříve užívalo k měření rychlosti střel. Může ho tvořit např. dřevěný hranol zavěšený na dvou dlouhých závěsech tak, aby se kýval jen ve svislé rovině.
Zápis
m = 4 g = 0,004 kg hmotnost střely v0 = 600 m·s-1 vstupní rychlost střely v1 = 100 m·s-1 výstupní rychlost střely M = 1 kg hmotnost kyvadla d = 25 cm = 0,25 m tloušťka kyvadla h = ? (m) výška, do které se kyvadlo vychýlí F = ? (N) velikost konstantní síly, která střelu v kyvadle brzdí Rozbor
Při řešení budeme předpokládat, že střela pronikne kyvadlem velmi rychle, a nebudeme uvažovat její odchylku od původního směru pohybu. Při řešení využijeme zákon zachování hybnosti (ZZH) a energie (ZZE).
Nápověda 1 - ZZH
Nakreslete si obrázek situace a napište ZZH pro soustavu střela a kyvadlo.
Nápověda 2 - ZZE
Napište ZZE pro soustavu střela a kyvadlo. Porovnejte energii v situaci těsně před nárazem střely do kyvadla a v situaci těsně poté, co střela opustí kyvadlo.
Nápověda 3 - ZZE pro kyvadlo
Napište, jaká je mechanická energie kyvadla bezprostředně poté, co ho opustí střela, a jaká v nejvyšším bodě, do kterého se vychýlí.
Nápověda 4 - brzdící síla a výška vychýlení kyvadla
K vyjádření brzdící síly a výšky, do které se kyvadlo vychýlí, využijte rovnice (1), (4) a (5).
Číselný výpočet
Je dáno:
\[m\,=\,4\,\mathrm{g}\,=\,0{,}004\, \mathrm{kg},\] \[v_0\,=\,600\,\mathrm{m \cdot s^{-1}},\] \[v_1\,=\,100\,\mathrm{m\cdot s^{-1}},\] \[g\,=\,9{,}81\,\mathrm{m\cdot s^{-2}},\] \[d\,=\,25\,\mathrm{cm}\,=\,0{,}25\,\mathrm{m},\] \[M\,=\,1\,\mathrm{kg}.\]Hledáme:
\[h\,=\,?,\] \[F\,=\,?,\] \[h\,=\,\frac {m^2\left(v_0-v_1\right)^2}{2gM^2},\] \[h\,=\,\frac {0{,}004^2\cdot\left(600-100\right)^2}{2{\cdot}9{,}81{\cdot}1^2}\,\mathrm{m},\] \[h\,=\,0{,}2\, \mathrm{m},\] \[F\,=\,\frac {m}{2d}\left[v_0^2-v_1^2\right],\] \[F\,=\,\frac {0{,}004}{2{\cdot}0{,}25}[600^2-100^2]\, \mathrm{N},\] \[F\,=\,2800\,\mathrm{N}\,\dot{=}\,2{,}8\, \mathrm{kN}.\]Celkové řešení
Při řešení budeme předpokládat, že střela pronikne kyvadlem velmi rychle, a nebudeme uvažovat její odchylku od původního směru pohybu. Při řešení využijeme zákon zachování hybnosti (ZZH) a energie (ZZE).
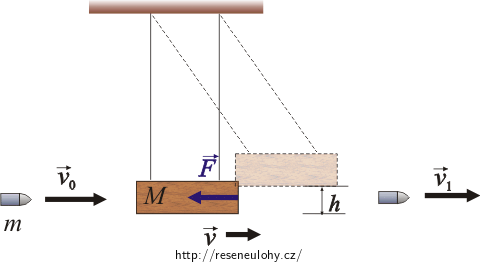
\(\vec{F}\).…konstantní brzdící síla
\(h\)…výška, do které se kyvadlo vychýlí
\(m\)…hmotnost střely
\(M\)…hmotnost kyvadla
\(\vec{v_0}\)…rychlost střely před proniknutím
\(\vec{v_1}\)…rychlost střely po proniknutí
\(\vec{v}\)…rychlost kyvadla po proniknutí střely
\[\mathrm{ZZH:}\hspace{15px} \vec{p_s}+\vec{p_k}\,=\,\vec{p_s^{'}}+\vec{p_k^{'}}\]\(\vec{p_\mathrm{s}}\)…hybnost střely před nárazem do kyvadla
\(\vec{p_\mathrm{k}}\)…hybnost kyvadla před nárazem střely
\(\vec{p_\mathrm{s}^{'}}\)…hybnost střely bezprostředně po průniku kyvadlem
\(\vec{p_\mathrm{k}^{'}}\)…hybnost kyvadla bezprostředně po průniku střely
\[m\vec{v_0}+0\,=\,m\vec{v_1}+M\vec{v}\]Skalárně:
\[mv_0\,=\,mv_1+Mv.\tag{1}\]Při zasažení kyvadla střelou se část kinetické energie střely promění na vnitřní energii kyvadla a střely, část na kinetickou energii střely po proniknutí a část na kinetickou energii kyvadla. Tedy:
\[\mathrm{ZZE:}\hspace{15px}\frac{1}{2}mv_0^2\,=\,\frac{1}{2}mv_1^2+\frac{1}{2}Mv^2+\Delta U,\tag{2}\]\(\Delta U\)…změna vnitřní energie.
Součet změny vnitřní energie a kinetické energie kyvadla je roven práci brzdící síly F na dráze d:
\[\Delta U+\frac{1}{2}Mv^2\,=\,Fd,\tag{3}\]\(d\)…tloušťka kvádru.
Ve vztahu (2) dosadíme za změnu vnitřní energie a kinetickou energii kyvadla vztah (3):
\[\frac{1}{2}mv_0^2\,=\,\frac{1}{2}mv_1^2+Fd.\tag{4}\]Kinetická energie kyvadla, kterou má poté, co ho opustí střela, se přemění na potenciální energii:
\[E_\mathrm{k}\,=\,E_\mathrm{p}\]\(E_\mathrm{k}\)…kinetická energie kyvadla po proniknutí střely
\(E_\mathrm{p}\)…potenciální energie kyvadla v nejvyšším bodě
\[\frac{1}{2}Mv^2=Mgh\tag{5}\]\(g\)…tíhové zrychlení
Z rovnice (1) vyjádříme rychlost kyvadla:
\[mv_0\,=\,mv_1+Mv,\tag{1}\] \[v\,=\,\frac{m\left(v_0-v_1\right)}{M}.\tag{6}\]Dosadíme ji do vztahu (5):
\[\frac{1}{2}Mv^2\,=\,Mgh,\] \[\frac{1}{2}M\frac{m^2\left(v_0-v_1\right)^2}{M^2}\,=\,Mgh\]a vyjádříme výšku h, do které se kyvadlo vychýlí:
\[h\,=\,\frac{m^2\left(v_0-v_1\right)^2}{2M^2g},\] \[h\,=\,\frac {0{,}004^2\cdot\left(600-100\right)^2}{2{\cdot}9{,}81{\cdot}1}\,\mathrm{m},\] \[h\,=\,0{,}2\, \mathrm{m}.\]Brzdící sílu vyjádříme ze vztahu (4):
\[\frac{1}{2}mv_0^2\,=\,\frac{1}{2}mv_1^2+Fd,\tag{4}\] \[F\,=\,\frac{1}{2d}mv_0^2-\frac{1}{2d}mv_1^2.\] \[F\,=\,\frac {m}{2d}[v_0^2-v_1^2],\] \[F\,=\,\frac {0{,}004}{2{\cdot}0{,}25}[600^2-100^2]\, \mathrm{N},\] \[F\,=\,2800\,\mathrm{N}\,\dot{=}\,2{,}8\, \mathrm{kN}.\]Odpověď:
Kyvadlo se vychýlí do výšky \(h\,=\,0{,}2\,\mathrm{m}\).
Brzdící síla, která na střelu v kyvadle působí, je \(F\,=\,2800\,\mathrm{N}\,\dot{=}\,2{,}8\, \mathrm{kN}\).
Odpověď
Kyvadlo se vychýlí do výšky \[h\,=\,\frac {m^2\left(v_0-v_1\right)^2}{2gM^2}\,=\,0{,}2\,\mathrm{m}.\]
Brzdící síla, která na střelu v kyvadle působí, je \[F\,=\,\frac {m}{2d}[v_0^2-v_1^2]\,=\,2800\,\mathrm{N}\,\dot{=}\,2{,}8\, \mathrm{kN}.\]






