Plavba voru
Úloha číslo: 125
Vor pluje přes řeku stálou rychlostí o velikosti w vzhledem k vodě kolmo na její proud. Šířka řeky je d. Předpokládejte, že voda unáší vor tak, že složka rychlosti voru vyvolaná proudící vodou je kvadraticky rostoucí v závislosti na vzdálenosti od břehů. U břehů je nulová, ve středu řeky má maximální hodnotu u.
Určete průběh rychlosti \(\vec{v}(t)\) voru vzhledem ke břehu a průběh jeho polohy \(\vec{r}(t)\).
Jaká je poloha místa, ve kterém vor přistane u druhého břehu?
Nápověda 1: Obrázek situace
Nakreslete si obrázek situace. Označte si v něm souřadné osy a pohyb voru si rozložte na dva pohyby, ve směru osy x (kolmo na proud) a ve směru osy y (po toku řeky).
Nakreslete si i průběh složky rychlosti voru vy vyvolané proudící vodou.
Nápověda 2: Průběh rychlosti voru
Vyjádřete si za pomoci obrázku z předchozí nápovědy složky rychlosti voru vx a vy.
Jakou funkcí vyjádříte rychlost ve směru osy y?
Nápověda 3: Průběh polohy voru
Znáte složky rychlosti voru. Určete z nich souřadnice voru a průběh jeho polohového vektoru.
Nápověda 4: Poloha místa přistání voru
Potřebujete zjistit souřadnice místa, ve kterém vor na druhém břehu přistane. Šířku řeky znáte, takže i souřadnici x. Znáte také složky rychlosti voru. Vyjádřete si čas, za který vor přejede řeku. Pak můžete určit i jaká bude v tomto čase souřadnice y.
CELKOVÉ ŘEŠENÍ:
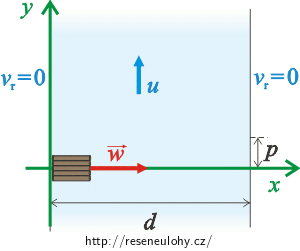
Obrázek 1 – situace:
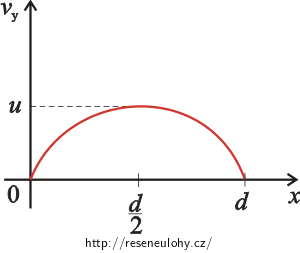
Obrázek 2 – průběh složky rychlosti vyvolané proudící vodou:
Na obrázku 1 je vr velikost rychlosti proudu řeky, velikost rychlosti voru vzhledem ke břehům máme označenou v, složky rychlosti voru jsou vx, vy.
Jedná se o skládání dvou pohybů (ve směru osy x a ve směru osy y).
Průběh rychlosti voru
Podle obrázků 1, 2 platí:
\[v_\mathrm{x}\,=\,w,\tag{1}\] \[v_\mathrm{y}\,=\,ax^{2}\,+\,bx\,+\,c.\tag{2}\]Průběh rychlosti voru ve směru osy y má tvar paraboly, popisuje ho kvadratická funkce.
Určení konstant a, b, c:
Na parabole leží body: \(\left[0,\,0\right],\) \(\left[\frac{d}{2},\,u\right],\) \(\left[d,\,0\right].\)
Dosazením bodu [0, 0] dostaneme:
\[c\,=\,0\,.\]Dosazením bodu \(\left[\frac{d}{2},\,u\right]\) dostaneme:
\[a\left(\frac{d}{2}\right)^{2}\,+\,b\frac{d}{2}\,=\,u\,.\tag{3}\]Dosazením bodu [d, 0] dostaneme:
\[ad^{2}\,+\,bd\,=\,0\,.\tag{4}\]Řešíme soustavu dvou rovnic o dvou neznámých a,b:
Z (4):
\[a\,=\, -\frac{b}{d}\,.\]Dosadíme do (3):
\[-\frac{bd^{2}}{4d} \,+\, \frac{bd}{2} \,=\, u,\] \[\frac{bd}{4} \,=\, u,\] \[b\,=\,\frac{4u}{d},\] \[a\,=\,-\frac{4u}{d^{2}}.\]Dosadíme za konstanty do (2):
\[v_\mathrm{y} \,=\, -\frac{4u}{d^{2}}x^{2}\,+\,\frac{4u}{d}x\,,\]kde z (1) \[x\,=\,wt\,,\]
\[v_\mathrm{y}\,=\,-\frac{4u}{d^{2}}w^{2}t^{2}\,+\,\frac{4u}{d}wt,\tag{5}\]
\[\vec{v}(t)\,=\,v_\mathrm{x}\vec{i} \,+\, v_\mathrm{y}\vec{j},\] \[\vec{v}(t)\,=\,w\vec{i}\,+\,\left(\frac{4u}{d}wt\,-\,\frac{4u}{d^{2}}w^{2}t^{2}\right)\vec{j},\]kde \(\vec{i}\), \(\vec{j}\) jsou jednotkové vektory ve směru souřadnicových os.
Průběh polohového vektoru voru
Složky rychlosti voru jsou podle (1) a (5):
\[v_\mathrm{x}\,=\,w,\] \[v_\mathrm{y}\,=\,-\frac{4u}{d^{2}}\,w^{2}t^{2}\,+\,\frac{4u}{d}\,wt.\]Souřadnice jsou pak:
\[x\,=\, wt,\] \[y\,=\,\int{v_\mathrm{y}}\,\mathrm{d}t\,=\,\int\left(-\frac{4u}{d^{2}}w^{2}t^{2}\,+\,\frac{4u}{d}wt\right)\,\mathrm{d}t\,=\, -\frac{4u}{3d^{2}}w^{2}t^{3}\,+\,\frac{4u}{2d}wt^{2}\,+\,k.\]Pro t = 0 s je y = 0 m, tedy k = 0:
\[y \,=\, -\,\frac{4u}{3d^{2}}\,w^{2}t^{3}\,+\,\frac{2u}{d}\,wt^{2},\tag{6}\]
\[\vec{r}(t)\,=\,x\vec{i}\,+\,y\vec{j}\,,\] \[\vec{r}(t)\,=\,wt\vec{i}\,+\,\left(\frac{2u}{d}\,wt^{2}\,-\,\frac{4u}{ 3d^{2}}\,w^{2}t^{3}\right)\vec{j}\,,\]kde \(\vec{i}\), \(\vec{j}\) jsou jednotkové vektory ve směru souřadnicových os.
Místo přistání voru
Vor se přes řeku dostane za čas \(t \,=\, \frac{d}{w}\), neboť rychlostí w ve směru osy x má urazit vzdálenost d.
Poloha místa, ve kterém vor přistane, má souřadnice:
\[x\,=\,d\,.\]Souřadnice y v čase \(t \,=\, \frac{d}{w}\) bude podle (6):
\[y \,=\, \frac{2uw}{d}t^{2}\,-\,\frac{4uw^{2}}{3d^{2}}t^{3} \,=\, \frac{2uw}{d}\,\frac{d^{2}}{w^{2}} \,-\,\frac{4uw^{2}}{3d^{2}}\,\frac{d^{3}}{w^{3}},\] \[y \,=\, \frac{2ud}{w} \,-\, \frac{4ud}{3w} \,=\, \frac{2ud}{3w}.\]Souřadnice místa, kde vor přistane, jsou:
\[x\,=\,d\,,\] \[y\,=\,\frac{2ud}{3w}\,.\]Odpověď
Průběh \(\vec{v}(t)\) rychlosti voru vzhledem ke břehu je:
\[\vec{v}(t)\,=\,w\vec{i}\,+\,\left(\frac{4u}{d}wt\,-\,\frac{4u}{d^{2}}w^{2}t^{2}\right)\vec{j}\,,\]kde \(\vec{i}\), \(\vec{j}\) jsou jednotkové vektory ve směru souřadnicových os.
Průběh \(\vec{r}(t)\) polohy voru je:
\[\vec{r}(t)\,=\,wt\vec{i}\,+\,\left(\frac{2u}{d}wt^{2}\,-\,\frac{4u}{ 3d^{2}}w^{2}t^{3}\right)\vec{j}\,,\]kde \(\vec{i}\), \(\vec{j}\) jsou jednotkové vektory ve směru souřadnicových os.
Poloha místa, ve kterém vor přistane u druhého břehu, je:
\[x\,=\,d\,,\] \[y\,=\,\frac{2ud}{3w}\,.\]




