Kutálení kuličky
Úloha číslo: 131
Malá kulička se skutálela po dráze tvaru nakloněné roviny délky l = 2 m, která svírá s vodorovnou rovinou úhel α = 30° a je zakončená obloukem o poloměru R = 0,4 m a středovém úhlu 90° (viz obrázek).
Velikost rychlosti, se kterou kulička opustila konec oblouku, byla v = 3,5 m·s−1 .
a) Určete maximální výšku H nad vodorovnou rovinou, do které se kulička dostane po opuštění dráhy.
b) Určete dobu T, po kterou se kulička nachází ve vzduchu po opuštění dráhy.
c) Určete vodorovnou vzdálenost L od místa, kde kulička opustí oblouk, k místu, na které dopadne.
Zápis
l = 2 m délka nakloněné roviny α = 30° úhel, který svírá nakloněná rovina s vodorovnou rovinou R = 0,4 m poloměr oblouku v = 3,5 m·s−1 rychlost, se kterou kulička opustila konec oblouku H = ? (m) maximální výška, do které se kulička dostane T = ? (s) doba, po kterou se kulička nachází ve vzduchu L = ? (m) vzdálenost, ve které kulička dopadne Z tabulek g = 9,81 m·s−2 tíhové zrychlení Nápověda 1: Obrázek situace
Jak můžete charakterizovat pohyb kuličky po opuštění dráhy?
Nakreslete si obrázek a vyznačte v něm veličiny, které budete k výpočtům potřebovat.
Napište si všechny potřebné vztahy mezi těmito veličinami, které vyplývají z obrázku.
Nápověda 2 pro a): Maximální výška
Jaké vztahy (pro souřadnice a složky rychlosti) platí pro vrh šikmo vzhůru s počáteční rychlostí velikosti v a elevačním úhlem 90° − α?
Jak z těchto vztahů vyjádříte maximální výšku, do které se kulička dostane po opuštění dráhy?
Nápověda 3 pro b): Doba letu kuličky
Celková doba, po kterou se kulička nachází ve vzduchu, se skládá z doby stoupání kuličky a z doby klesání kuličky.
Jak tyto doby vypočítáte?
Nápověda 4 pro c): Délka letu
Vodorovnou vzdálenost od místa, kde kulička opustí oblouk, si označte L a vyznačte si ji v obrázku.
Jak ji vypočítáte?
CELKOVÉ ŘEŠENÍ:
a) Výška výstupu
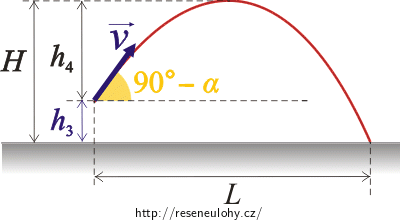
Jedná se o vrh šikmo vzhůru z počáteční výšky h3 nad vodorovnou rovinou pod úhlem 90° − α s počáteční rychlostí \(\vec{v}\) (viz obrázek 1).
Obrázek 1:
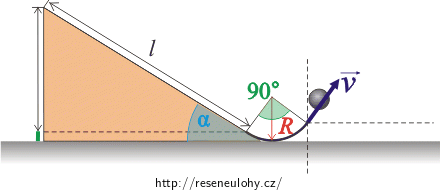
Obrázek 2:
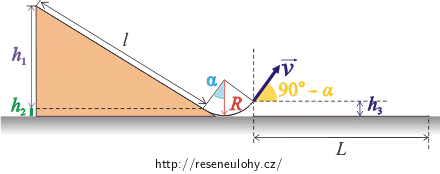
Z obrázků 1, 2 vyplývá několik vztahů pro úhel α a dané hodnoty:
\[h_1\,=\,l\sin\alpha\,,\] \[h_2\,=\,R\left(1\,-\,\cos\alpha\right)\,,\] \[h_3\,=\,R\left[1\,-\,\cos(90^{\circ}-\alpha)\right]\,=\,R\left(1\,-\,\sin\alpha\right)\,,\] \[H\,=\,h_3\,+\,h_4\,.\]Pro vrh šikmo vzhůru s počáteční rychlostí v a elevačním úhlem 90° − α pak dostáváme:
\[v_\mathrm{x}\,=\,v\,\cos(90^{\circ}-\alpha)\,=\,v\,\sin\alpha\,,\] \[v_\mathrm{y}=v\sin(90^{\circ}-\alpha)-gt=v\cos\alpha-gt\,,\] \[x\,=\,vt\,\sin\alpha\,,\] \[y\,=\,vt\,\cos\alpha\,-\,\frac{1}{2}gt^{2}\,.\]Pro maximální výšku:
\[v_\mathrm{y}\,=\,0\,,\] \[t_\mathrm{v}\,=\,\frac{v\,\cos\alpha}{g}\,,\] \[h_4\,=\, vt_\mathrm{v}\,\cos\alpha\,-\,\frac{1}{2}gt_\mathrm{v}^{2} \,=\, \frac{v^{2}\,\cos^{2}\alpha}{g}\,-\,\frac{gv^{2}\,\cos^{2}\alpha}{2g^{2}}\,=\,\frac{v^{2}\,\cos^{2}\alpha}{2g}\,,\] \[H \,=\, h_3 \,+\, h_4 \,=\, R\,\left(1\,-\,\sin\alpha\right)\,+\,\frac{v^{2}\,\cos^{2}\alpha}{2g}\,.\]Číselně:
\[H\,=\,\left[0{,}4\,\left(1\,-\,\frac{1}{2}\right)\,+\,\frac{3{,}5^{2}\cdot \left(\frac{\sqrt{3}}{2}\right)^{2}}{2{\cdot} 9{,}81}\right]\,\mathrm{m}\,,\] \[H\,\dot=\,0{,}67\,\mathrm{m}\,.\]b) Doba letu
Doba stoupání:
\[t_\mathrm{v}\,=\,T_1\,=\,\frac{v\,\cos\alpha}{g}\,.\]Doba klesání (kulička padá z výšky H):
\[H\,=\,\frac{1}{2}gT_2^{2}\,,\] \[T_2\,=\,\sqrt{\frac{2H}{g}}\,.\]Celková doba letu:
\[T\,=\,T_1\,+\,T_2\,=\,\frac{v\,\cos\alpha}{g}\,+\,\sqrt{\frac{2H}{g}}\,.\]Číselně:
\[T\,=\,\left[\frac{3{,}5\cdot\frac{\sqrt{3}}{2}}{9{,}81}\,+\,\sqrt{\frac{2{\cdot} 0{,}67}{9{,}81}}\right]\,\mathrm{s}\,,\] \[T\,\dot=\,0{,}68\,\mathrm{s}\,.\]c) Délka letu
Ve vodorovném směru se kulička pohybuje rovnoměrně přímočaře rychlostí v sin α po dobu T.
Vodorovná vzdálenost L od místa, kde kulička opustí oblouk, je tedy:
\[L\,=\,vT\,\sin\alpha\,.\]Číselně:
\[L=\left(3{,}5{\cdot} 0{,}68\cdot \frac{1}{2}\right)\,\mathrm{m}\,,\] \[L\,\dot=\,1{,}19\,\mathrm{m}\,.\]Odpověď
a) Pro maximální výšku nad vodorovnou rovinou, do které se kulička dostane po opuštění dráhy, platí:
\[H\,=\,R\left(1\,-\,\sin\alpha\right)\,+\,\frac{v^{2}\,\cos^{2}\alpha}{2g}\,\dot=\,0{,}67\,\mathrm{m}\,.\]b) Doba, po kterou se kulička nachází ve vzduchu po opuštění dráhy, je:
\[T\,=\,T_1\,+\,T_2\,=\,\frac{v\,\cos\alpha}{g}\,+\,\sqrt{\frac{2H}{g}}\,\dot=\,0{,}68\,\mathrm{s}\,.\]c) Vodorovná vzdálenost od místa, kde kulička opustí oblouk, je:
\[L\,=\,vT\,\sin\alpha\,\dot=\,1{,}19\,\mathrm{m}\,.\]