Těžiště různě uspořádaných soustav koulí

Úloha číslo: 1130

Určete polohu těžiště soustavy složené ze čtyř homogenních koulí o hmotnostech 1 kg, 2 kg, 3 kg a 4 kg v těchto případech:

A) koule leží na přímce ve stejných vzdálenostech,

B) koule leží ve vrcholech čtverce,

C) koule jsou umístěny ve čtyřech sousedních vrcholech krychle.

Ve všech případech jsou vzdálenosti mezi středy sousedních koulí rovny a. V případech B) a C) je nejtěžší koule v počátku souřadného systému.

Zápis

m₁ = 1 kg	hmotnost 1. koule
m₂ = 2 kg	hmotnost 2. koule
m₃ = 3 kg	hmotnost 3. koule
m₄ = 4 kg	hmotnost 4. koule
a	vzdálenost mezi středy libovolných dvou sousedních koulí
r_T = ?	poloha těžiště

Nápověda 1 (k části A)
Nakreslete si obrázek zachycující situaci a vhodně do něj zaveďte souřadný systém. Středům S₁, S₂, S₃, S₄ všech koulí připište ve vašem systému odpovídající souřadnice.
Řešení nápovědy 1
Jedno možné zavedení souřadného systému a umístění koulí ukazuje obrázek níže.

V tomto zavedení jsou souřadnice středů koulí:
\[S_1\,=\,[0{,}0,0],\] \[S_2\,=\,[a,0{,}0],\] \[S_3\,=\,[2a,0{,}0],\] \[S_4\,=\,[3a,0{,}0].\]
Nápověda 2 (k části A)
Umíte nyní bez počítání okamžitě určit y-ovou a z-ovou souřadnici těžiště?
Řešení nápovědy 2
Vzhledem k tomu, že středy (a tedy i těžiště) všech koulí leží na ose x, bude také těžiště celé soustavy ležet na ose x. Každý bod na ose x má ovšem y-ovou i z-ovou souřadnici nulovou:
\[y_\mathrm{T}\,=\,z_\mathrm{T}\,=\,0.\]
Zbývá tedy určit pouze x-ovou souřadnici těžiště.
Nápověda 3 (k části A)
Koule bez udaných rozměrů můžeme považovat za hmotné body, jejichž hmotnost je soustředěna do středů původních koulí. Využijeme tedy vztah pro výpočet polohy (polohového vektoru) těžiště soustavy hmotných bodů. Znáte jej? Jak se změní, zajímáme-li se již pouze o x-ovou souřadnici těžiště?
Řešení nápovědy 3
Vztah pro polohu těžiště soustavy n hmotných bodů vypadá následovně:
\[\vec{r}_\mathrm{T}\,=\,\frac{\sum_{i=1}^n{m_\mathrm{i}\vec{r}_\mathrm{i}}}{\sum_{i=1}^n{m_\mathrm{i}}},\]
kde m_i jsou hmotnosti jednotlivých hmotných bodů a r_i jim příslušející polohové vektory.

Protože souřadnice těžiště lze počítat po složkách, platí pro x-ovou souřadnici těžiště naší soustavy:
\[x_\mathrm{T}\,=\,\frac{\sum_{i=1}^4{m_\mathrm{i}x_\mathrm{i}}}{\sum_{i=1}^4{m_\mathrm{i}}}.\tag{1}\]
Souřadnice x_i zde znamená vzdálenost i-té koule od počátku souřadného systému.
Nápověda 4 (k části A)
Rozepište sumy ve vztahu (1) dle zadaných hodnot a dopočítejte souřadnici x_T.
Řešení nápovědy 4
Rozepsáním sum ve vztahu (1) dostáváme:
\[x_\mathrm{T}\,=\,\frac{m_1{\cdot}0\,+\,m_2{\cdot}a\,+\,m_3{\cdot}2a\,+\,m_4{\cdot}3a}{m_1\,+\,m_2\,+\,m_3\,+\,m_4}.\tag{2}\]
Nakonec číselně dosadíme do vztahu (2) hmotnosti ze zadání:
\[x_\mathrm{T}\,=\,\frac{1{\cdot}0\,+\,2{\cdot}a\,+\,3{\cdot}2a\,+\,4{\cdot}3a}{1\,+\,2\,+\,3\,+\,4}\,=\,\frac{20a}{10}\,=\,2a.\]
Těžiště T soustavy zadané v části A má souřadnice:
\[T\,=\,[2a,0{,}0].\]
Nápověda 5 (k části B)
Postupujte v části B stejně jako v části předchozí – nakreslete si obrázek a umístěte koule do souřadného systému (nezapomeňte, že nejhmotnější z nich má své místo v počátku soustavy souřadnic). Napište souřadnice středů koulí a výpočtem nebo úvahou rozhodněte, zda lze některou ze souřadnic těžiště určit přímo, bez výpočtu.
Řešení nápovědy 5
Jedno možné zavedení souřadného systému a umístění koulí ukazuje obrázek níže.

V tomto zavedení jsou souřadnice středů koulí:
\[S_1\,=\,[0,a,0],\] \[S_2\,=\,[a,a,0],\] \[S_3\,=\,[a,0{,}0],\] \[S_4\,=\,[0{,}0,0].\]
Vzhledem k tomu, že středy (a tedy i těžiště) všech koulí leží v rovině xy, bude také těžiště celé soustavy ležet v rovině xy. Každý bod této roviny má ovšem z-ovou souřadnici nulovou, tedy pro těžiště platí:
\[z_\mathrm{T}\,=\,0.\]
Zbývá tedy určit pouze x-ovou a y-ovou souřadnici těžiště.
Nápověda 6 (k části B)
K výpočtu x-ové a y-ové souřadnice těžiště použijte opět vztah (1), resp. jeho obměnu pro proměnnou y. Číselně obě souřadnice dopočítejte.
Řešení nápovědy 6
Pro x-ovou souřadnici těžiště x_T dle vztahu (1) platí:
\[x_\mathrm{T}\,=\,\frac{\sum_{i=1}^4{m_\mathrm{i}x_\mathrm{i}}}{\sum_{i=1}^4{m_\mathrm{i}}}\,=\,\frac{m_1{\cdot}0\,+\,m_2{\cdot}a\,+\,m_3{\cdot}a\,+\,m_4{\cdot}0}{m_1\,+\,m_2\,+\,m_3\,+\,m_4}.\]
Číselně:
\[x_\mathrm{T}\,=\,\frac{1{\cdot}0\,+\,2{\cdot}a\,+\,3{\cdot}a\,+\,4{\cdot}0}{1\,+\,2\,+\,3\,+\,4}\,=\,\frac{5a}{10}\,=\,\frac{a}{2}.\]
Pro výpočet y-ové souřadnice těžiště y_T použijeme vztah analogický vztahu (1), pouze pro proměnnou y:
\[y_\mathrm{T}\,=\,\frac{\sum_{i=1}^4{m_\mathrm{i}y_\mathrm{i}}}{\sum_{i=1}^4{m_\mathrm{i}}}\,=\,\frac{m_1{\cdot}a\,+\,m_2{\cdot}a\,+\,m_3{\cdot}0\,+\,m_4{\cdot}0}{m_1\,+\,m_2\,+\,m_3\,+\,m_4}.\]
Číselně:
\[y_\mathrm{T}\,=\,\frac{1{\cdot}a\,+\,2{\cdot}a\,+\,3{\cdot}0\,+\,4{\cdot}0}{1\,+\,2\,+\,3\,+\,4}\,=\,\frac{3a}{10}.\]
Těžiště T soustavy zadané v části B má souřadnice:
\[T\,=\,[\frac{a}{2},\frac{3a}{10},0].\]
Nápověda 7 (k části C)
Stejný postup zopakujte také potřetí, v části C. Nakreslete si obrázek, umístěte koule do souřadného systému, určete jejich souřadnice a dle vztahu (1) či jeho obměn (pro jiné souřadnice než x) určete postupně x_T, y_T, z_T.
Řešení nápovědy 7
Jedno možné zavedení souřadného systému a umístění koulí ukazuje obrázek níže.

V tomto zavedení jsou souřadnice středů koulí:
\[S_1\,=\,[0,a,0],\] \[S_2\,=\,[0{,}0,a],\] \[S_3\,=\,[a,0{,}0],\] \[S_4\,=\,[0{,}0,0].\]
Pro x-ovou souřadnici těžiště x_T dle vztahu (1) platí:
\[x_\mathrm{T}\,=\,\frac{\sum_{i=1}^4{m_\mathrm{i}x_\mathrm{i}}}{\sum_{i=1}^4{m_\mathrm{i}}}\,=\,\frac{m_1{\cdot}0\,+\,m_2{\cdot}0\,+\,m_3{\cdot}a\,+\,m_4{\cdot}0}{m_1\,+\,m_2\,+\,m_3\,+\,m_4}\,=\,\frac{3a}{10}.\]
Pro y-ovou souřadnici těžiště y_T analogicky platí:
\[y_\mathrm{T}\,=\,\frac{\sum_{i=1}^4{m_\mathrm{i}y_\mathrm{i}}}{\sum_{i=1}^4{m_\mathrm{i}}}\,=\,\frac{m_1{\cdot}a\,+\,m_2{\cdot}0\,+\,m_3{\cdot}0\,+\,m_4{\cdot}0}{m_1\,+\,m_2\,+\,m_3\,+\,m_4}\,=\,\frac{a}{10}.\]
Pro z-ovou souřadnici těžiště z_T analogicky platí:
\[z_\mathrm{T}\,=\,\frac{\sum_{i=1}^4{m_\mathrm{i}z_\mathrm{i}}}{\sum_{i=1}^4{m_\mathrm{i}}}\,=\,\frac{m_1{\cdot}0\,+\,m_2{\cdot}a\,+\,m_3{\cdot}0\,+\,m_4{\cdot}0}{m_1\,+\,m_2\,+\,m_3\,+\,m_4}\,=\,\frac{a}{5}.\]
Těžiště T soustavy zadané v části C má souřadnice:
\[T\,=\,[\frac{3a}{10},\frac{a}{10},\frac{a}{5}].\]
Komentář
Všechny získané výsledky se vztahují k námi zvoleným souřadným systémům a umístěním koulí, které jsou znázorněny na obrázcích. Při jiném umístění koulí do souřadných systémů se budou vaše výsledky číselně lišit!
Celkové řešení
Koule bez udaných rozměrů můžeme považovat za hmotné body, jejichž hmotnost je soustředěna do středů původních koulí. Na úvod každé části úlohy je nutné umístit soustavu koulí do vhodně zvoleného souřadného systému.

Část A:

Jedno možné zavedení souřadného systému a umístění koulí ukazuje obrázek níže.

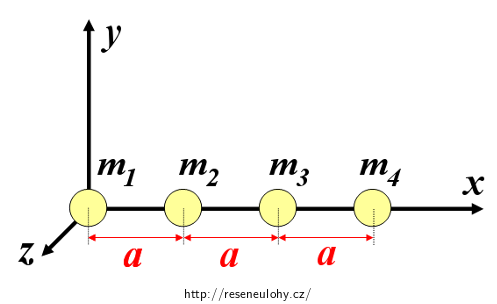
V tomto zavedení jsou souřadnice středů koulí:
\[S_1\,=\,[0{,}0,0],\] \[S_2\,=\,[a,0{,}0],\] \[S_3\,=\,[2a,0{,}0],\] \[S_4\,=\,[3a,0{,}0].\]
Vzhledem k tomu, že středy (a tedy i těžiště) všech koulí leží na ose x, bude také těžiště celé soustavy ležet na ose x. Každý bod na ose x má ovšem y-ovou i z-ovou souřadnici nulovou:
\[y_\mathrm{T}\,=\,z_\mathrm{T}\,=\,0.\]
Zbývá tedy určit pouze x-ovou souřadnici těžiště.

Vztah pro polohu těžiště soustavy n hmotných bodů vypadá následovně:
\[\vec{r}_\mathrm{T}\,=\,\frac{\sum_{i=1}^n{m_\mathrm{i}\vec{r}_\mathrm{i}}}{\sum_{i=1}^n{m_\mathrm{i}}},\]
kde m_i jsou hmotnosti jednotlivých hmotných bodů a r_i jim příslušející polohové vektory. Protože souřadnice těžiště lze počítat po složkách, platí pro x-ovou souřadnici těžiště naší soustavy:
\[x_\mathrm{T}\,=\,\frac{\sum_{i=1}^4{m_\mathrm{i}x_\mathrm{i}}}{\sum_{i=1}^4{m_\mathrm{i}}}.\tag{1}\]
Rozepsáním sum ve vztahu (1) dostáváme:
\[x_\mathrm{T}\,=\,\frac{m_1{\cdot}0\,+\,m_2{\cdot}a\,+\,m_3{\cdot}2a\,+\,m_4{\cdot}3a}{m_1\,+\,m_2\,+\,m_3\,+\,m_4}.\tag{2}\]
Nakonec číselně dosadíme do vztahu (2) hmotnosti ze zadání:
\[x_\mathrm{T}\,=\,\frac{1{\cdot}0\,+\,2{\cdot}a\,+\,3{\cdot}2a\,+\,4{\cdot}3a}{1\,+\,2\,+\,3\,+\,4}\,=\,\frac{20a}{10}\,=\,2a.\]
Těžiště T soustavy zadané v části A má souřadnice:
\[T\,=\,[2a,0{,}0].\]

Část B:

Jedno možné zavedení souřadného systému a umístění koulí ukazuje obrázek níže.

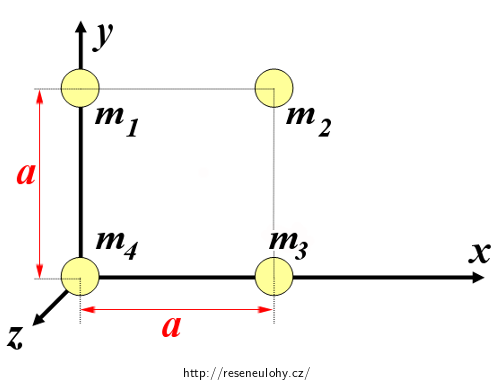
V tomto zavedení jsou souřadnice středů koulí:
\[S_1\,=\,[0,a,0],\] \[S_2\,=\,[a,a,0],\] \[S_3\,=\,[a,0{,}0],\] \[S_4\,=\,[0{,}0,0].\]
Vzhledem k tomu, že středy (a tedy i těžiště) všech koulí leží v rovině xy, bude také těžiště celé soustavy ležet v rovině xy. Každý bod této roviny má ovšem z-ovou souřadnici nulovou, tedy pro těžiště platí:
\[z_\mathrm{T}\,=\,0.\]
Zbývá tedy určit pouze x-ovou a y-ovou souřadnici těžiště.

Pro x-ovou souřadnici těžiště x_T dle vztahu (1) platí:
\[x_\mathrm{T}\,=\,\frac{\sum_{i=1}^4{m_\mathrm{i}x_\mathrm{i}}}{\sum_{i=1}^4{m_\mathrm{i}}}\,=\,\frac{m_1{\cdot}0\,+\,m_2{\cdot}a\,+\,m_3{\cdot}a\,+\,m_4{\cdot}0}{m_1\,+\,m_2\,+\,m_3\,+\,m_4}.\]
Číselně:
\[x_\mathrm{T}\,=\,\frac{1{\cdot}0\,+\,2{\cdot}a\,+\,3{\cdot}a\,+\,4{\cdot}0}{1\,+\,2\,+\,3\,+\,4}\,=\,\frac{5a}{10}\,=\,\frac{a}{2}.\]
Pro výpočet y-ové souřadnice těžiště y_T použijeme vztah analogický vztahu (1), pouze pro proměnnou y:
\[y_\mathrm{T}\,=\,\frac{\sum_{i=1}^4{m_\mathrm{i}y_\mathrm{i}}}{\sum_{i=1}^4{m_\mathrm{i}}}\,=\,\frac{m_1{\cdot}a\,+\,m_2{\cdot}a\,+\,m_3{\cdot}0\,+\,m_4{\cdot}0}{m_1\,+\,m_2\,+\,m_3\,+\,m_4}.\]
Číselně:
\[y_\mathrm{T}\,=\,\frac{1{\cdot}a\,+\,2{\cdot}a\,+\,3{\cdot}0\,+\,4{\cdot}0}{1\,+\,2\,+\,3\,+\,4}\,=\,\frac{3a}{10}.\]
Těžiště T soustavy zadané v části B má souřadnice:
\[T\,=\,[\frac{a}{2},\frac{3a}{10},0].\]

Část C:

Jedno možné zavedení souřadného systému a umístění koulí ukazuje obrázek níže.

V tomto zavedení jsou souřadnice středů koulí:
\[S_1\,=\,[0,a,0],\] \[S_2\,=\,[0{,}0,a],\] \[S_3\,=\,[a,0{,}0],\] \[S_4\,=\,[0{,}0,0].\]
Pro x-ovou souřadnici těžiště x_T dle vztahu (1) platí:
\[x_\mathrm{T}\,=\,\frac{\sum_{i=1}^4{m_\mathrm{i}x_\mathrm{i}}}{\sum_{i=1}^4{m_\mathrm{i}}}\,=\,\frac{m_1{\cdot}0\,+\,m_2{\cdot}0\,+\,m_3{\cdot}a\,+\,m_4{\cdot}0}{m_1\,+\,m_2\,+\,m_3\,+\,m_4}\,=\,\frac{3a}{10}.\]
Pro y-ovou souřadnici těžiště y_T analogicky platí:
\[y_\mathrm{T}\,=\,\frac{\sum_{i=1}^4{m_\mathrm{i}y_\mathrm{i}}}{\sum_{i=1}^4{m_\mathrm{i}}}\,=\,\frac{m_1{\cdot}a\,+\,m_2{\cdot}0\,+\,m_3{\cdot}0\,+\,m_4{\cdot}0}{m_1\,+\,m_2\,+\,m_3\,+\,m_4}\,=\,\frac{a}{10}.\]
Pro z-ovou souřadnici těžiště z_T analogicky platí:
\[z_\mathrm{T}\,=\,\frac{\sum_{i=1}^4{m_\mathrm{i}z_\mathrm{i}}}{\sum_{i=1}^4{m_\mathrm{i}}}\,=\,\frac{m_1{\cdot}0\,+\,m_2{\cdot}a\,+\,m_3{\cdot}0\,+\,m_4{\cdot}0}{m_1\,+\,m_2\,+\,m_3\,+\,m_4}\,=\,\frac{a}{5}.\]
Těžiště T soustavy zadané v části C má souřadnice:
\[T\,=\,[\frac{3a}{10},\frac{a}{10},\frac{a}{5}].\]
Poznámka: Všechny získané výsledky se vztahují k námi zvoleným souřadným systémům a umístěním koulí, které jsou znázorněny na obrázcích. Při jiném umístění koulí do souřadných systémů se budou vaše výsledky číselně lišit!
Odpověď
V námi zvolených souřadných systémech a umístěních koulí jsme vypočítali souřadnice těžiště následovně:
Část A: \[T\,=\,[2a,0{,}0].\] Část B: \[T\,=\,[\frac{a}{2},\frac{3a}{10},0].\] Část C: \[T\,=\,[\frac{3a}{10},\frac{a}{10},\frac{a}{5}].\]