Válec ponořený ve vodě
Úloha číslo: 149
Dřevěný válec plave ponořený ve vodě do 2/3 své výšky. Jakou práci je nutno vykonat na vytažení válce tak, že jeho spodní podstava se zvedne do výšky 20 cm nad hladinu? Poloměr válce je 10 cm a jeho výška 60 cm.
Zápis
r = 10 cm = 0,1 m poloměr válce h = 60 cm = 0,6 m výška válce x = 2/3h ponořená část válce a = 20 cm = 0,2 m výška nad hladinou, do které zvedáme válec W = ? (J) práce potřebná na zvednutí válce Nápověda 1 - plovoucí válec
Nakreslete si obrázek plovoucího válce a síly, které na něj působí. Co pro ně platí?
Nápověda 2 - síla potřebná na vytahování válce
Nakreslete si situaci, kdy je válec povytažený o výšku x z vody. Jaké síly na něj nyní působí? Jak velkou silou musíme válec přidržovat, aby se nepotopil?
Nápověda 3 - Práce na vytažení na úroveň hladiny
Jakou práci vykonáme při vytažení válce na úroveň hladiny? Znáte sílu, kterou válec vytahujeme, a dráhu, po které ho vytahujeme. Uvědomte si, že síla není konstantní, ale závisí na výšce povytažení.
Nápověda 4 - práce potřebná na vyzvednutí nad hladinu
Jak velkou práci vykonáme při zvednutí válce z úrovně hladiny do výšky a? Jaká bude celková práce?
Číselný výpočet
Dáno:
\[r\,=\,10\,\mathrm{cm}\,=\,0{,}1\,\mathrm{m},\] \[h\,=\,60\,\mathrm{cm}\,=\,0{,}6\,\mathrm{m},\] \[a\,=\,20\,\mathrm{cm}\,=\,0{,}2\,\mathrm{m},\] \[g\,=\,9{,}81\,\mathrm{m \cdot s^{-2}},\] \[\rho_\mathrm{v}\,=\,1000\,\mathrm{kg\,m^{-3}}.\]Hledáme:
\[W\,=\,?,\] \[W\,=\,\frac{2}{3}\rho_\mathrm{v} \pi r^2gh\left(\frac{1}{3}h+a\right),\] \[W\,=\,\frac {2}{3}\cdot1000{\cdot}3{,}14{\cdot} 0{,}1^2{\cdot}9{,}81{\cdot} 0{,}6\cdot\left(\frac{1}{3}\cdot0{,}6+0{,}2\right)\,\mathrm{J},\] \[W\,=\,49\,\mathrm{J}.\]Celkové řešení
Nejprve si rozmyslíme, jaké síly působí na válec, když plave, a co pro síly v této situaci platí.
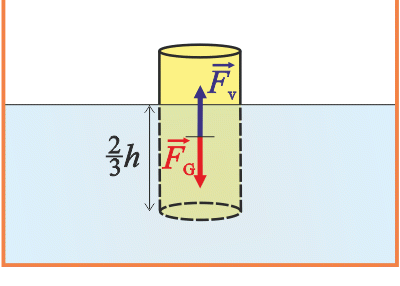
\(\vec{F_\mathrm{G}}\)…tíhová síla
\(\vec{F_\mathrm{v}}\)…vztlaková síla
\(h\)…výška válce
Když válec plave, je tíhová síla v rovnováze se vztlakovou silou.
Platí:
\[F_\mathrm{G}\,=\,F_\mathrm{v},\] \[mg\,=\,V_\mathrm{p}\rho_\mathrm{v} g,\]\(m\)…hmotnost válce,
\(g\)…tíhové zrychlení,
\(V_\mathrm{p}\)…objem ponořené části válce,
\(\rho_\mathrm{v}\)…hustota vody.
Hmotnost válce vyjádříme pomocí jeho hustoty a objemu:
\[\rho_\mathrm{d} V_\mathrm{v}g\,=\,V_\mathrm{p}\rho_\mathrm{v} g,\]\(\rho_\mathrm{d}\)…hustota dřeva,
\(V_\mathrm{v}\)…objem válce.
Objem válce a jeho ponořené části ještě vyjádříme pomocí výšky a plochy podstavy a zjistíme vztah mezi hustotou dřeva a vody:
\[\rho_\mathrm{d}Shg\,=\,\rho_\mathrm{v}S\frac{2}{3}h g,\] \[\rho_\mathrm{d}\,=\,\frac{2}{3}\rho_\mathrm{v}.\tag{1}\]Nyní rozebereme situaci, kdy je válec povytažený z vody o výšku x.
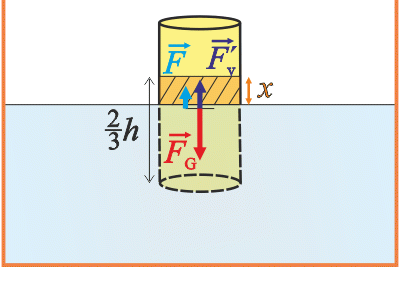
\(\vec{F_\mathrm{G}}\)…tíhová síla,
\(\vec{F_\mathrm{v}^{'}}\)…vztlaková síla,
\(\vec{F}\)…síla, kterou válec vytahujeme.
Povytáhneme-li válec o výšku x z vody, zmenší se ponořený objem válce, a tím i vztlaková síla, která na něj působí. Předpokládáme-li, že válec vytahujeme rovnoměrným pohybem, musíme ho v této situaci přidržovat silou, jejíž velikost je rovna právě úbytku vztlakové síly:
\[F\,=\,V_\mathrm{x}\rho_\mathrm{v}g\,=\,S\rho_\mathrm{v}gx.\tag{2}\]Síla, kterou válec vytahujeme, je úměrná jeho povytažení z vody.
Proměnná síla působí ve směru posunutí. Práci můžeme spočítat podle vztahu:
\[W_1\,=\,\int_\mathrm{x_1}^\mathrm{x_2}{F\mathrm{d}x}.\]Za F dosadíme ze vztahu (2), válec vytahujeme od x1 = 0 do x2 = 2/3 h.
\[W_1\,=\,\int_{0}^{\frac{2}{3}h}{S\rho_\mathrm{v}gx\mathrm{d}x}\,=\,S\rho_\mathrm{v}g\int_{0}^{\frac{2}{3}h}{x\mathrm{d}x},\] \[W_1\,=\,S\rho_\mathrm{v}g\left[\frac{x^{2}}{2}\right]_{0}^{\frac{2}{3}h}=S\rho_\mathrm{v}g\frac{2}{9}h^2,\] \[W_1\,=\,\frac{2}{9}\pi r^2\rho_\mathrm{v}h^2g.\tag{3}\]Poznámka: Grafické řešení
Práci potřebnou na vytažení válce z vody můžeme také určit s pomocí grafu závislosti síly F na výšce povytažení válce z vody x.
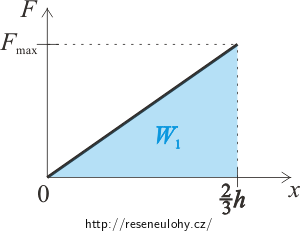
Plave-li válec ve vodě, je x = 0 a síla F = 0. Při vytažení válce na úroveň hladiny je \(x\,=\,\frac{2}{3}h\) a válec musíme držet silou Fmax, která je rovna jeho tíze:
\[F_\mathrm{max}\,=\,F_\mathrm{G}\,=\,mg\,=\,\rho_\mathrm{d} Vg=\frac{2}{3}\rho_\mathrm{v} \pi r^2hg.\]Práce je rovna obsahu plochy pod křivkou. Platí tedy:
\[W_1\,=\,\frac{F_\mathrm{max}\frac{2}{3}h}{2}\,=\,\frac{2}{9}\rho_\mathrm{v} \pi r^2h^2g.\]Práce, kterou musíme vykonat na zvednutí válce do výšky a nad hladinu, je rovna přírůstku potenciální energie válce:
\[W_2\,=\,\Delta E_\mathrm{p},\] \[W_2\,=\,mga,\] \[W_2\,=\,\rho_\mathrm{d}V_\mathrm{v}ga.\]Za \(\rho_\mathrm{d}\) dosadíme ze vztahu (1):
\[W_2\,=\,\frac{2}{3}\rho_\mathrm{v} \pi r^2 hga.\tag{4}\]Celková práce je rovna součtu práce potřebné na vytažení z vody a práce potřebné na zvednutí nad hladinu:
\[W\,=\,W_1+W_2,\] \[W\,=\,\frac{2}{9}\rho_\mathrm{v} \pi r^2h^2g+\frac{2}{3}\rho_\mathrm{v} \pi r^2 hga\,=\,\frac{2}{3}\rho_\mathrm{v} \pi r^2gh\left(\frac{1}{3}h+a\right),\] \[W\,=\,\frac {2}{3}\cdot1000{\cdot}3{,}14{\cdot} 0{,}1^2{\cdot}9{,}81{\cdot} 0{,}6(\frac{1}{3}\cdot0{,}6+0{,}2)\,\mathrm{J},\] \[W\,=\,49\,\mathrm{J}.\]Opdověď: Práce potřebná na zvednutí válce do výšky 20 cm je \(W\,=\,49\,\mathrm{J}.\)
Odpověď
Práce potřebná na zvednutí válce do výšky 20 cm je \[W=\frac{2}{3}\rho_\mathrm{v} \pi r^2gh\left(\frac{1}{3}h+a\right)\,=\,49\,\mathrm{J}.\]





