Přes příkop
Úloha číslo: 2265
Přes příkop je položené prkno délky \(L\) a hmotnosti \(M\). Vypočítejte, jak velké síly budou působit na prkno v místech A a B, kde se opírá o hrany příkopu, kráčí-li po něm člověk o hmotnosti \(m\) a nachází se:
a) ve třetině prkna,
b) ve středu prkna.
Rozbor
Nakresleme si obrázek situace.

Víme, že prkno je v klidu (neposouvá se, ani se neotáčí). Úkolem je určit velikost sil působících na něj v bodech A a B. Do obrázku vyznačíme všechny síly působící na prkno. K řešení následně využijeme podmínky rovnováhy pro síly a momenty sil, které říkají, že výslednice sil i výslednice momentů sil (vzhledem k libovolně zvolenému bodu) musí být nulové. Člověka budeme považovat za hmotný bod.
Nápověda 1
Nakreslete si obrázek a vyznačte do něj všechny síly působící na prkno. Člověka uvažujte jako hmotný bod v dané vzdálenosti od jednoho z bodů. Nezapomeňte, že prkno je také hmotné. Co platí pro výslednici sil působících na prkno, je-li v klidu?
Nápověda 2
Připomeňte si, jak je definovaný moment síly a jak zapíšeme jeho velikost. Rozmyslete si, co platí pro celkový moment sil, které působí na prkno.
Řešení a)
Nakreslíme si obrázek, do kterého vyznačíme všechny síly působící na prkno.
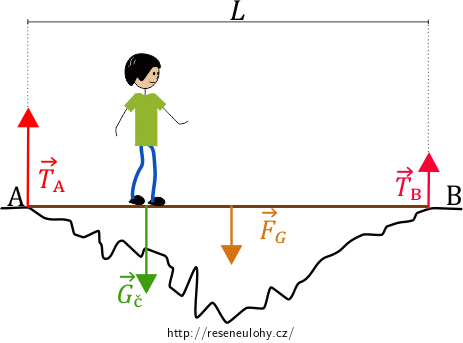
V bodě A, kde se prkno dotýká země, působí tlaková síla podložky \(\vec{T_\mathrm{A}}\) směrem kolmo vzhůru. Pro jednoduchost uvažujme člověka jako hmotný bod. Člověk se nachází ve vzdálenosti \(\frac{1}{3}L\) od bodu A a působí na prkno silou \(\vec{G_\mathrm{č}}\). V těžišti prkna, tedy ve vzdálenosti \(\frac{1}{2}L\) od bodu A, působí na prkno tíhová síla \(\vec{F_\mathrm{G}}\). V bodě B, kde je opřený druhý konec prkna, působí tlaková síla \(\vec{T_\mathrm{B}}\) opět kolmo vzhůru.
Prkno se nepohybuje, je v klidu, tzn. že výslednice všech sil působících na prkno musí být nulová. Platí tedy:
\[ \vec{T_\mathrm{A}} + \vec{T_\mathrm{B}} + \vec{G_\mathrm{č}} + \vec{F_\mathrm{G}} = 0. \]
Pro velikosti sil pak platí:
\[ T_\mathrm{A} + T_\mathrm{B} - G_\mathrm{č} - F_\mathrm{G} = 0. \tag{1}\]
Tíhu člověka a tíhovou sílu působící na prkno dokážeme určit. Ovšem stále máme jednu rovnici o dvou neznámých. K určení obou sil potřebujeme ještě jednu rovnici. Víme, že se prkno neotáčí. Výsledný moment sil působících na prkno musí být tedy nulový. Jako druhou rovnici využijeme momentovou větu.
Moment síly vzhledem ke zvolenému bodu určíme jako
\[\vec M = \vec r \times \vec F,\]
kde \(\vec F\) je působící síla a \(\vec r\) je polohový vektor, který začíná ve zvoleném bodě a míří do působiště síly \(\vec F\).
Momenty budeme vztahovat vzhledem k bodu A. (Proč je zrovna bod A vhodný, si lze přečíst v poznámce.) To znamená, že polohové vektory budou vycházet z tohoto bodu a budou vždy směřovat do působiště síly, jejíž moment síly určujeme. Pro sílu \(\vec {G_{č}}\) je rameno síly \(\vec {r_č}\) zakresleno v následujícím obrázku (viz obr. 3).
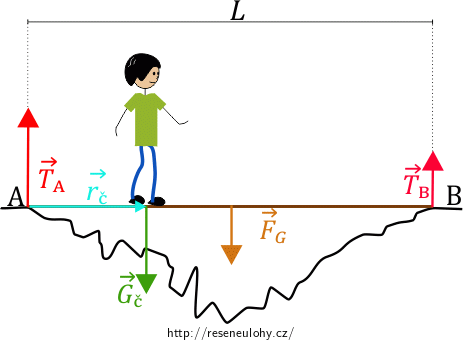
Velikost vektorového součinu, a tedy i momentu síly, můžeme zapsat jako
\[M = rF\sin{\alpha} ,\]
kde \(\alpha\) je úhel mezi polohovým vektorem a působící silou. Z obrázku je jasné, že síla \(\vec {G_{č}}\) a vektor \(\vec {r_č}\) svírají pravý úhel, a tedy sinus je roven 1. V tomto případě je velikost vektoru \(r_č\) rovna přímo ramenu síly, které udává kolmou vzdálenost bodu, k němuž moment vztahujeme od vektorové přímky síly.
Pro určení směru momentu síly používáme pravidlo pravé ruky, kdy prsty ukazují ve směru polohového vektoru a sklápí se do směru vektoru dané síly. Odtažený palec pak ukazuje směr momentu síly. Zvolme si, že s kladným znaménkem budeme uvažovat moment síly směřující do obrazovky. Nyní můžeme sestavit druhou rovnici pomocí momentové věty.
Moment síly \(T_\mathrm{A}\) je vzhledem k bodu A nulový, protože je nulové rameno této síly. Všechny ostatní síly svírají se svými rameny pravý úhel, dostáváme tedy:
\[\frac{1}{3}LG_\mathrm{č} + \frac{1}{2}LF_\mathrm{G} - LT_\mathrm{B} = 0.\tag{2}\]
Získali jsme soustavu dvou rovnic (1) a (2). Do obou dosadíme za \(G_\mathrm{č}\) a \(F_\mathrm{G}\) podle zadání:
\[T_\mathrm{A} + T_\mathrm{B} -mg-Mg=0,\]
\[\frac{1}{3}Lmg + \frac{1}{2}LMg - LT_\mathrm{B} = 0.\]
Z druhé rovnice dokážeme ihned vyjádřit \(T_\mathrm{B}\):
\[ T_\mathrm{B} = g(\frac{m}{3} + \frac{M}{2} ).\]
Získaný výsledek můžeme dosadit do první rovnice soustavy a vyjádřit \(T_\mathrm{A}\):
\[T_\mathrm{A} =mg + Mg - g(\frac{m}{3} + \frac{M}{2} )=g(\frac{2m}{3} + \frac{M}{2} ).\]
Řešení b)
Začněme opět nakreslením obrázku s vyznačenými silami.
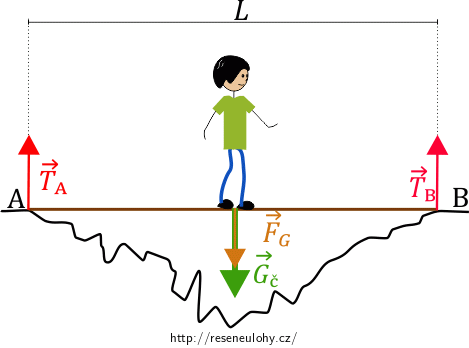
Můžeme postupovat obdobně jako v případě a) úlohy. Prkno je stále v klidu, výslednice sil je nulová. Zachováme kladné znaménko u sil směřujících nahoru a sestavíme rovnici pro velikosti sil:
\[T_\mathrm{A} + T_\mathrm{B} − G_\mathrm{č} − F_\mathrm{G} = 0.\tag{3}\]
Vidíme, že rovnice je stejná jako (1). Směr sil se nijak nezměnil, jedinou prozatím známou změnou (o velikosti sil \(\vec {T_\mathrm{A}}\) a \(\vec {T_\mathrm{B}}\) zatím nic nevíme) je poloha člověka a tím způsobený posun působiště síly \(\vec {G_\mathrm{č}}\).
Dál využijeme momentovou větu. Opět volíme kladné znaménko pro směr momentu síly do obrazovky. Momenty sil budeme vztahovat opět k bodu A, v rovnici (2) tak dojde k jediné změně, a sice velikosti vektoru \(\vec {r_\mathrm{č}}\). Působiště síly \(\vec {G_\mathrm{č}}\) se nyní nachází ve vzdálenosti \(\frac{1}{2}L\) od bodu A. Proto rovnice pro velikost celkového momentu síly bude vypadat následovně:
\[\frac{1}{2}LG_\mathrm{č} + \frac{1}{2}LF_\mathrm{G} - LT_\mathrm{B} = 0.\tag{4}\]
V rovnicích (3) a (4) vyjádříme velikosti sil \(G_\mathrm{č}\) a \(F_\mathrm{G}\). Dostaneme soustavu dvou rovnic o dvou neznámých:
\[{T_\mathrm{A}} + {T_\mathrm{B}} − mg − Mg = 0,\tag{5a}\]
\[\frac{m+M}{2}g - T_\mathrm{B} = 0.\tag{5b}\]
Z rovnice (5b) můžeme hned vyjádřit velikost síly \(T_\mathrm{B}\) a dosadit do rovnice (5a), ze které určíme \(T_\mathrm{B}\):
\[ T_\mathrm{B} =\frac{m+M}{2}g,\]
\[{T_\mathrm{A}} + \frac{m+M}{2}g − mg − Mg = 0,\]
\[{T_\mathrm{A}} = g(m+M) − \frac{m+M}{2}g,\]
\[{T_\mathrm{A}} = \frac{m+M}{2}g.\]
Odpověď a)
Jestliže člověk stojí v jedné třetině desky (blíže k bodu A), jsou velikosti sil působících v bodech A a B:
\[T_\mathrm{A}=g( \frac{2m}{3}+ \frac{M}{2}),\]
\[T_\mathrm{B}=g( \frac{m}{3}+ \frac{M}{2}).\]
Odpověď b)
Jestliže se člověk nachází ve středu desky, působí v bodech A a B síly o velikosti:
\[T_\mathrm{A}=T_\mathrm{B}=g \frac{M+m}{2}.\]
Poznámka: Proč jsme momenty sil vztahovali k bodu A?
V úloze jsme zvolili za vztažný bod pro momenty sil bod A. Proč jsme ho vybrali? Nemohli jsme zvolit jiný bod?
V zásadě je jedno, který z bodů zvolíme, některé jsou ale výhodnější, jiné méně. Šikovné je volit vztažný bod např. v působišti některé ze sil. Pak je její moment nulový, protože je nulové i její rameno a z rovnice pro momenty nám vypadne.
Pokud bychom za vztažný bod zvolili působiště tíhy člověka nebo tíhové síly působící na prkno, dostali bychom se ke stejnému výsledku, jen druhá rovnice by obsahovala obě neznámé. To by znamenalo o něco delší počítání a více úprav soustavy rovnic.
Zatímco při volbě jednoho z bodů působení našich neznámých sil, tedy A nebo B, jsme se jedné neznámé v rovnici zbavili díky nulovému rameni síly a z druhé rovnice soustavy jsme mohli hned vyjádřit jednu neznámou.
Volba bodu B by byla stejně účinná jako bodu A. V kombinaci s námi zvoleným kladným směrem momentu síly by vycházela opačná znaménka; z druhé rovnice soustavy bychom dostali neznámou \(T_\mathrm{A}\) namísto \(T_\mathrm{B}\).
Kontrola: A je to dobře?
Po vyřešení úlohy je dobré se na výsledky kriticky podívat a zhodnotit, zda je pro úlohu možné, aby takovým způsobem vyšla.
V řešení a) nám vyšla síla \(T_\mathrm{A}\) větší než \(T_\mathrm{B}\). Přičemž člověk stál blíž k bodu A. To je očekávatelný výsledek, protože větší část zátěže se nachází právě blíž k bodu A – na tomto konci je prkno namáháno více než u konce B.
Bude-li se člověk přibližovat k bodu B, síla v bodě A se bude zmenšovat a v bodě B zvětšovat. Podle této úvahy by pro člověka nacházejícího se ve středu desky měla nastat rovnost sil v bodě A a B. Podle výsledků části b) úlohy tomu tak skutečně je.

