Dřevěný hranol
Úloha číslo: 156
Dřevěný hranol o hmotnosti 3 kg leží na vodorovné podložce. Je zasažen střelou o hmotnosti 5 g pohybující se vodorovně. Střela v hranolu zůstane. Hranol se posune po podložce o 25 cm. Koeficient tření mezi hranolem a podložkou je 0,2. Určete počáteční rychlost střely.
Zápis
M = 3 kg hmotnost dřevěného hranolu m = 5 g = 5·10-3 kg hmotnost střely d = 25 cm = 0,25 m posunutí hranolu po podložce f = 0,2 koeficient tření mezi hranolem a podložkou v0 = ? (m·s-1) rychlost střely před zásahem hranolu Rozbor
K řešení úlohy využijeme zákon zachování hybnosti, pomocí kterého určíme rychlost hranolu po zásahu střelou, a zákon zachování energie.
Nápověda 1 - zákon zachování hybnosti (ZZH)
Nakreslete si obrázek situace. Napište, jaká je hybnost soustavy střela + hranol těsně před zásahem hranolu střelou a těsně po něm. Co pro tyto hybnosti platí?
Nápověda 2 - zákon zachování energie (ZZE)
Uvědomte si, na co se přemění kinetická energie, kterou má střela před zasažením hranolu.
Nápověda 3 - zastavení hranolu
Proč se hranol, který se dal po zásahu do pohybu, po čase zastaví? Na co se přemění jeho kinetická energie?
Číselný výpočet
Je dáno:
\[m=5\,\mathrm{g}=0{,}005\,\mathrm{kg},\] \[M=3\,\mathrm{kg},\] \[g=9{,}81\,\mathrm{m \cdot s^{-2}},\] \[d=25\,\mathrm{cm}=0{,}25\,\mathrm{m},\] \[f=0{,}2.\]Hledáme:
\[v_0=?,\] \[v_0=\frac{m+M}{m}\sqrt{2gdf},\] \[v_0=\frac{0{,}005+3}{0{,}005}\sqrt{2{\cdot}9{,}81{\cdot}0{,}25{\cdot}0{,}2}\,\mathrm{m \cdot s^{-1}},\] \[v_0=595\,\mathrm{m \cdot s^{-1}}. \]Odpověď
Střela se před zásahem hranolu pohybovala rychlostí \[v_0\,=\,\frac{m+M}{m}\sqrt{2gdf}\,=\,595\,\mathrm{m \cdot s^{-1}}.\]
Celkové řešení
K řešení úlohy využijeme zákon zachování hybnosti, pomocí kterého určíme rychlost hranolu po zásahu střelou, a zákon zachování energie.

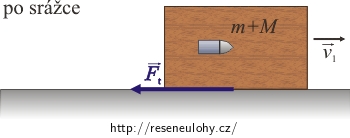
Podle zákona zachování hybnosti bude hybnost střely a hranolu před zásahem rovna hybnosti hranolu se střelou po zásahu:
\[\mathrm{ZZH:} \qquad \vec{p_0}+ \vec{p_h}=\vec{p_1}.\]p0…hybnost střely před zásahem
ph…hybnost hranolu před zásahem
p1…hybnost soustavy střela+hranol po zásahu
\[m\vec{v_0}+ 0\,=\,\left(m+M\right)\vec{v_1}\]v0…rychlost střely před zásahem
v1…rychlost soustavy střela+hranol po zásahu
Protože se střela i hranol pohybují v jedné přímce, můžeme ZZH přepsat skalárně:
\[mv_0\,=\,\left(m+M\right)v_1.\]Odtud vyjádříme rychlost v1:
\[v_1\,=\,\frac{mv_0}{m+M}.\tag{1}\]Část kinetické energie střely se přemění na kinetickou energii hranolu, který se dá po zásahu do pohybu. Další část kinetické energie střely se přemění na vnitřní energii střely a hranolu, které se při zásahu zahřejí. Zapíšeme to rovnicí:
\[E_\mathrm{ks}\,=\,E_\mathrm{k}+\Delta U,\]Eks…kinetická energie střely před zásahem,
Ek…kinetická energie soustavy střela+hranol těsně po zásahu,
ΔU…změna vnitřní energie střely a hranolu,
\[\frac{1}{2}mv_0^2,=\,\frac{1}{2}\left(M+m\right)v_1^2+\Delta U.\]Hranol, který se dal po zásahu střelou do pohybu, se po čase zastaví. Zapíšeme, co se stane s jeho kinetickou energií. Hranol se zastaví díky působení třecí síly. Třecí síla při zastavování hranolu koná práci, hranol i podložka se zahřívají a zvyšuje se jejich vnitřní energie. Kinetická energie hranolu se střelou, kterou má bezprostředně po zásahu, je rovna práci, kterou vykoná třecí síla na dráze zastavení.
\[E_\mathrm{k}\,=\,W\]Ek…kinetická energie soustavy střela+hranol těsně po zásahu
W…práce třecí síly
\[\frac{1}{2}\left(m+M\right)v_1^2\,=\,F_\mathrm{t}d\tag{2}\]Třecí síla je úměrná kolmé tlakové síle, kterou působí hranol se střelou na podložku:
\[F_\mathrm{t} \,=\, Nf \,=\, \left(M+m\right)gf.\]Dosadíme za třecí sílu do vztahu (2):
\[\frac{1}{2}\left(m+M\right)v_1^2\,=\,\left(M+m\right)gfd.\]Za v1 dosadíme ze vztahu (1):
\[\frac{1}{2}\left(M+m\right)\frac{m^2v_0^2}{\left(M+m\right)^2}\,=\,\left(M+m\right)gfd,\] \[v_0^2\,=\,\frac{2\left(M+m\right)^2}{m^2}gfd,\] \[v_0\,=\,\frac{M+m}{m}\sqrt{2gfd},\] \[v_0\,=\,\frac{0{,}005+3}{0{,}005}\sqrt{2{\cdot}9{,}81{\cdot}0{,}25{\cdot}0{,}2}\,\mathrm{m \cdot s^{-1}},\] \[v_0\,=\,595\,\mathrm{m \cdot s^{-1}}. \]Odpověď: Střela se před zásahem hranolu pohybovala rychlostí \[v_0\,=\,595\,\mathrm{m \cdot s^{-1}}.\]






