Trosečníci
Úloha číslo: 914
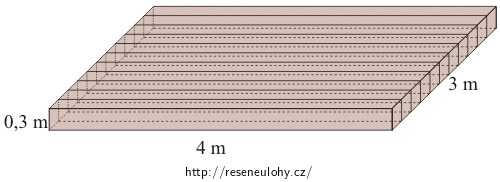
Dva trosečníci vypluli na voru, který si zhotovili z trámů. Délka voru je 4 m, šířka je 3 m, výška je 30 cm (viz obr.). Hustota dřeva, ze kterého je vor vyroben, je 600 kg/m3.
a) Potopí se vor s trosečníky, kteří i se zásobami váží 210 kg?
b) Mohou trosečníci přibrat ještě jednoho trosečníka, který váží 75 kg, aniž by se potopili?
c) Jakou maximální hmotnost mohou mít další trosečníci, kteří by přistoupili na vor, aby se vor ještě nepotopil?
Zápis
d = 4 m délka voru s = 3 m šířka voru v = 30 cm= 0,3 m výška voru ρ = 600 kg/m3 hustota dřeva m1 = 210 kg hmotnost trosečníků a zásob m2 = 75 kg hmotnost dalšího trosečníka Z tabulek: ρ = 1025 kg/m3 hustota mořské vody g = 10 N/kg číslo, kterým musíme vynásobit hmotnost, abychom dostali příslušnou gravitační sílu K části a: nápověda 1
Jaké síly působí na vor s trosečníky a jakým směrem?
K části a: nápověda 2
Jak vypočteme gravitační sílu působící na vor a trosečníky? Co k tomu ještě potřebujeme určit a jak to uděláme (uvědomte si, jaké údaje o voru znáte)?
K části a: nápověda 3
Na čem závisí vztlaková síla působící na vor? Jak ji vypočteme?
K části a: nápověda 4
Jak určíme, jaká část voru je nyní potopena? Uvědomte si, jaké jsou podmínky rovnováhy voru, a zapište je. Odtud již zjistíte objem ponořené části voru.
K části a: nápověda 5
Porovnejte objem V' ponořené části voru s celkovým objemem V voru (V budete muset dopočítat). Co z toho plyne?
K části b: nápověda 1
Co se změní po přistoupení dalšího trosečníka na vor a jak?
K části b: nápověda 2
Budeme postupovat obdobně jako v části a). Zajímá nás tedy, jaký bude nyní objem V'' ponořené části voru. Určete ho.
K části b: nápověda 3
Porovnejte objem V'' ponořené části voru s celkovým objemem V voru. Co z toho plyne?
K části c: nápověda 1
Popište, co je krajním případem, od kdy se začne vor potápět? Máme na mysli především objem ponořené části voru.
K části c: nápověda 2
Jaké síly působí na vor s trosečníky, co pro ně platí?
K části c: nápověda 3
Uvědomte si, co v rovnici (8) znáte nebo už jste vypočítali v předchozích úkolech a co chcete určit. Pomůže vám, když si rozepíšete, jak se síly v rovnici (8) vypočítají.
K části c: nápověda 4
Vyjádřete z rovnice (9) maximální hmotnost dalšího trosečníka a dopočítejte ji.
Celkové řešení
Část a):
Na vor s trosečníky působí směrem nahoru síla vztlaková a směrem dolů síla gravitační.
Gravitační síla je součtem gravitačních sil působících na jednotlivé trosečníky a samotný vor. Vypočte se podle vztahu:
\[F_\mathrm{g}\,=\,mg\,,\tag{1}\]kde m je hmotnost daného tělesa a g = 10 N/kg (číslo, kterým musíme vynásobit hmotnost, abychom dostali příslušnou gravitační sílu).
Potřebujeme tedy ještě určit hmotnost voru. To uděláme pomocí znalosti rozměrů voru a hustoty dřeva, ze kterého je vyroben:
\[m_\mathrm{voru}\,=\,\rho_\mathrm{D}{\cdot}V\,=\,\rho_\mathrm{D}{\cdot}s{\cdot}v{\cdot}d,\tag{2}\]kde ρD je hustota dřeva, s je šířka voru, v je výška voru a d je délka voru.
Číselná hodnota je:
\[m_\mathrm{voru}\,=\,600{\cdot}3{\cdot}0{,}3{\cdot}4\,\mathrm{kg}\,=\,2160\,\mathrm{kg}\,.\]Celková gravitační síla působící na vor s trosečníky bude:
\[F_\mathrm{g}\,=\,(m_\mathrm{voru} + m_1)g\,,\]kde m1 je hmotnost trosečníků se zásobami (210 kg) a mvoru je hmotnost voru.
Vztlaková síla působící na vor závisí na hustotě ρ okolní kapaliny, tedy mořské vody (hustotu mořské vody najdeme v tabulkách: ρ = 1025 kg/m3), na objemu V' ponořené části voru a na konstantě g = 10 N/kg (číslo, kterým musíme vynásobit hmotnost, abychom dostali příslušnou gravitační sílu). Vypočteme ji jako:
\[F_\mathrm{v}\,=\,V'{\rho}g\,. \tag{3}\]
Vor je v rovnováze, jestliže jsou vztlaková a gravitační síla vyrovnané. Proto můžeme napsat rovnici:
\[F_\mathrm{g}\,=\,F_\mathrm{v} \]a dosadit do ní za Fg a Fv ze vztahů (1) a (3), tím máme:
\[(m_\mathrm{voru}\,+\,m_1){\cdot}g\,=\,V'{\cdot}{\rho}{\cdot}g\,,\] \[(m_\mathrm{voru}\,+\,m_1)\,=\,V'{\cdot}{\rho}\,.\]Protože známe všechno kromě objemu V' ponořené části voru, můžeme tento objem z rovnice vyjádřit a dopočítat:
\[V'\,=\,\frac{(m_\mathrm{voru}\,+\,m_1)}{{\rho}}.\tag{4}\]Číselně:
\[V'\,=\,\frac{(2160\,+\,210)}{1025}\,\mathrm{m^3}\,\dot=\,2{,}31\,\mathrm{m^3}\,.\]Objem voru V určíme jako:
\[V \,=\,s{\cdot}v{\cdot}d\,,\tag{5}\]kde s je šířka voru, v je jeho výška a d jeho délka.
Číselně:
\[V\,=\,3{\cdot}0{,}3{\cdot}4\mathrm{m^3}\,=\,3{,}6\,\mathrm{m^3}\,.\]Platí \(V'\)<\(V\), takže vor trosečníky i s nákladem unese a nepotopí se.
Část b):
Po přistoupení dalšího trosečníka se zvětší celková hmotnost trosečníků a voru; na plavidlo bude tedy působit větší gravitační síla a vor se více ponoří.
Opět vycházíme z rovnosti gravitační a vztlakové síly, jedině tak se vor nebude hýbat nahoru ani dolů. Označíme je jinak, aby se nám nepletly se silami v části a). Tedy:
\[F_\mathrm{g2}\,=\,F_\mathrm{v2}\,,\] \[(m_\mathrm{voru}\,+\,m_1\,+\,m_2){\cdot}g\,=\,V''{\cdot}\rho{\cdot}g\,,\] \[(m_\mathrm{voru}\,+\,m_1\,+\,m_2)\,=\,V''{\cdot}\rho \,,\tag{6}\]kde mvoru je hmotnost voru, m1 hmotnost původních trosečníků se zásobami a m2 je hmotnost dalšího trosečníka (75 kg), V'' je objem ponořené části voru a g = 10 N/kg (číslo, kterým musíme vynásobit hmotnost, abychom dostali příslušnou gravitační sílu).
Z rovnice (6) vyjádříme:
\[V''\,=\,\frac{(m_\mathrm{voru}\,+\,m_1\,+\,m_2)}{\rho}\tag{7}\]a vypočteme. Číselná hodnota je:
\[V''\,=\,\frac{(2160\,+\,210\,+\,75)}{1025}\,\mathrm{m^3}\,\dot=\,2{,}39\,\mathrm{m^3}\,.\]Platí \(V''\)<\(V\), takže trosečníci mohou na palubu voru přibrat ještě dalšího trosečníka.
Část c):
Krajním případem, kdy se vor začne potápět, je stav, kdy je pod vodou celý objem voru, ale trosečníci a věci na voru jsou ještě nad vodou. Tuto situaci nyní budeme uvažovat pro další výpočty.
Víme, že směrem dolů působí gravitační síla, která je součtem dílčích gravitačních sil – viz část a). Teď ale neznáme gravitační sílu působící na další trosečníky, protože neznáme jejich hmotnost (tu právě chceme určit).
Směrem nahoru působí na vor vztlaková síla vody. Opět musí platit, že aby byl vor s trosečníky v rovnováze, výslednice sil, které na něj působí, musí být nulová. Musí platit (opět volíme jiné značení než v předchozích částech):
\[F_\mathrm{v3}\,=\,F_\mathrm{g3}\,.\tag{8}\]Rovnici (8) dále rozepíšeme na:
\[V{\cdot}\rho{\cdot}g\,=\,(m_\mathrm{voru}\,+\,m_1\,+\,m_\mathrm{max}){\cdot}g\,,\] \[V{\cdot}\rho\,=\,(m_\mathrm{voru}\,+\,m_1\,+\,m_\mathrm{max})\,,\tag{9}\]kde V je objem celého voru (tedy V = s·d·v),
ρ je hustota mořské vody (hustotu mořské vody najdeme v tabulkách: ρ = 1025 kg/m3),
mvoru je hmotnost voru (určeno v a)),
m1 hmotnost původních trosečníků se zásobami a mmax je maximální hmotnost dalších trosečníků, aby se vor ještě nepotopil,
g = 10 N/kg (číslo, kterým musíme vynásobit hmotnost, abychom dostali příslušnou gravitační sílu).
Skoro všechny veličiny v rovnici (9) známe, neznáme pouze mmax. Tuto veličinu tedy vyjádříme:
\[m_\mathrm{max}\,=\,V{\cdot}\rho\,-\,m_\mathrm{voru}\,-\,{m_1}\,.\]Číselná hodnota je:
\[m_\mathrm{max}\,=\,(0{,}3{\cdot}4{\cdot}3{\cdot}1025\,-\,210\,-\,2160)\,\mathrm{kg}\,=\,1320\,\mathrm{kg}\,.\]Další trosečníci by mohli vážit až 1320 kg.
Odpověď
a) Vor s trosečníky se nepotopí.
b) Dalšího trosečníka lze na vor přibrat.
c) Další trosečníci by mohli mít maximální hmotnost 1320 kg.







