Pád Země

Úloha číslo: 1241

Jak dlouho by trval pád Země ke Slunci, kdyby Země náhle ztratila svou oběžnou rychlost?

Obrázek k zadání

  • Zápis

    \(v=0 \mathrm{\frac{km}{s}}\) oběžná rychlost Země
    \(t= ?\) doba pádu Země ke Slunci

  • Nápověda 1

    Využitím zákona zachování energie sestavte pohybovou rovnici pro Zemi.

  • Nápověda 2

    Jak se dá pomocí vzdálenosti \(r\) a času \(t\) vyjádřit rychlost \(v_\mathrm{p}\)?

    Dosaďte tento vztah pro rychlost \(v_\mathrm{p}\) do rovnice (5), rozmyslete si, jak se mění vzdálenost \(r\) a vyjádřete čas \(t\).

  • Nápověda 3

    Dle http://www.wolframalpha.com/ platí: \[\int{\sqrt{\frac{r}{R_\mathrm{ZS}-r}}}\mathrm{d}r=\frac {\sqrt{\frac{r}{R_\mathrm{ZS}-r}} \left(\sqrt{r} \left(r-R_\mathrm{ZS} \right) + R_\mathrm{ZS}\sqrt{R_\mathrm{ZS}-r}  \mathrm{arctg}\,{\sqrt{\frac{r}{R_\mathrm{ZS}-r}}} \right) }{\sqrt {r}}+c,\] kde \(c\) je konstanta.

    Využitím derivace ověřte, zda to platí.

  • Nápověda 4

    Ověřili jsme, že platí \[\int{\sqrt{\frac{r}{R_\mathrm{ZS}-r}}}\mathrm{d}r= -\sqrt{r\left(R_\mathrm{ZS}-r\right)}+R_\mathrm{ZS} \mathrm{arctg}\,{\sqrt{\frac{r}{R_\mathrm{ZS}-r}}}+c.\] Využijte toho a dopočítejte čas \(t\) ze vztahu (6).

  • Celkové řešení

    Sestavení pohybové rovnice pro Zemi

     

    Ze zákona zachování energie víme, že součet kinetické energie \(E_\mathrm{k}\) a potenciální energie \(E_\mathrm{p}\) se nemění. Je tedy roven počáteční energii Země \(E_\mathrm{0}\): \[E_\mathrm{k}+E_\mathrm{p}=E_\mathrm{0}.\tag{1}\] Kinetická energie \(E_\mathrm{k}\) je rovna: \[E_\mathrm{k}=\frac{1}{2}M_\mathrm{Z}v_\mathrm{p}^2,\tag{2}\] kde \(M_\mathrm{Z}\) je hmotnost Země a \(v_\mathrm{p}\) je velikost rychlosti padající Země v daném okamžiku.

    Obrázek k řešení nápovědy

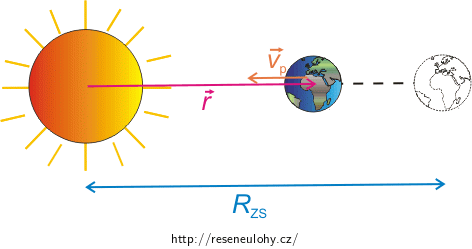
    Potenciální energie Země \(E_\mathrm{p}\) ve vzdálenosti \(r\) od Slunce je: \[E_\mathrm{p}=-\kappa \frac{M_\mathrm{Z}M_\mathrm{S}}{r},\tag{3}\] kde \(\kappa\) je gravitační konstanta a \(M_\mathrm{S}\) je hmotnost Slunce.

    Počáteční potenciální energie \(E_\mathrm{0}\) je rovna: \[ E_\mathrm{0}=-\kappa \frac{M_\mathrm{Z}M_\mathrm{S}}{R_\mathrm{ZS}},\tag{4}\] kde \(R_\mathrm{ZS}\) je vzdálenost Země od Slunce na začátku, když je Země ještě v klidu.

    Dosadíme (2), (3) a (4) do (1) a dostáváme pohybovou rovnici:

    \[\frac{1}{2}M_\mathrm{Z}v_\mathrm{p}^2-\kappa \frac{M_\mathrm{Z}M_\mathrm{S}}{r}=-\kappa \frac{M_\mathrm{Z}M_\mathrm{S}}{R_\mathrm{ZS}}.\]

    Obě strany rovnice vydělíme \(M_\mathrm{Z}\) a dostaneme: \[\frac{1}{2}v_\mathrm{p}^2-\kappa \frac{M_\mathrm{S}}{r}=-\kappa \frac{M_\mathrm{S}}{R_\mathrm{ZS}}.\tag{5}\]

     

    Vyjádření rychlosti \(v_\mathrm{p}\) a poté času \(t\)

     

    Rychlost \(v_\mathrm{p}\) můžeme vyjádřit jako derivaci vzdálenosti \(r\) podle času \(t\): \[v_\mathrm{p}=\frac{\mathrm{d}r}{\mathrm{d}t}.\]

    Dosadíme tento vztah do rovnice (5): \[\frac{1}{2}\left(\frac{\mathrm{d}r}{\mathrm{d}t}\right)^2-\kappa \frac{M_\mathrm{S}}{r}=-\kappa \frac{M_\mathrm{S}}{R_\mathrm{ZS}}.\]

    K oběma stranám rovnice přičteme \(\kappa \frac{M_\mathrm{S}}{r}\): \[\frac{1}{2}\left(\frac{\mathrm{d}r}{\mathrm{d}t}\right)^2=\kappa \frac{M_\mathrm{S}}{r}-\kappa \frac{M_\mathrm{S}}{R_\mathrm{ZS}}.\] Obě strany rovnice vynásobíme \(2\) a odmocníme: \[\left|\frac{\mathrm{d}r}{\mathrm{d}t}\right|=\sqrt{2\left(\kappa \frac{M_{S}}{r}-\kappa \frac{M_\mathrm{S}}{R_\mathrm{ZS}}\right)}.\]

    Vytkneme \(\kappa M_\mathrm{S}\): \[\left|\frac{\mathrm{d}r}{\mathrm{d}t}\right|=\sqrt{2\kappa M_\mathrm{S}\left( \frac{1}{r} - \frac{1}{R_\mathrm{ZS}} \right)}=\sqrt{2\kappa M_\mathrm{S}}\sqrt{ \frac{1}{r} - \frac{1}{R_\mathrm{ZS}}}.\]

    Obě strany rovnice vynásobíme \(\frac{\left|\mathrm{d}t\right|}{\sqrt{2\kappa M_\mathrm{S}}\sqrt{ \frac{1}{r} - \frac{1}{R_\mathrm{ZS}}}}\) a prohodíme levou a pravou stranu rovnice: \[\left| \mathrm{d}t \right|=\frac{\left|\mathrm{d}r\right|}{\sqrt{2\kappa M_\mathrm{S}}\sqrt{ \frac{1}{r} - \frac{1}{R_\mathrm{ZS}}}}.\]

    Vzdálenost \(r\) se s rostoucím časem \(t\) zmenšuje, proto po odstranění absolutních hodnot pro naši úlohu dostáváme: \[ \mathrm{d}t =\frac{-\mathrm{d}r}{\sqrt{2\kappa M_{S}}\sqrt{ \frac{1}{r} - \frac{1}{R_\mathrm{ZS}}}}.\]

    Obě strany rovnice integrujeme: \[t =\int_{R_\mathrm{ZS}}^{R_\mathrm{Z}+R_\mathrm{S}}{ \frac{-\mathrm{d}r}{\sqrt{2\kappa M_{S}}\sqrt{ \frac{1}{r} - \frac{1}{R_\mathrm{ZS}}}}},\] kde \(R_\mathrm{Z}\) je poloměr Země a \(R_\mathrm{S}\) je poloměr Slunce.

    Na začátku \(r\) odpovídá vzdálenosti \(R_\mathrm{ZS}\) a ve chvíli, kdy Země dopadne na Slunce, tak \(r\) je rovno součtu poloměru Země a Slunce \(R_\mathrm{Z}+R_\mathrm{S}\). Proto jsme zvolili meze integrálu \(R_\mathrm{ZS}\) a \(R_\mathrm{Z}+R_\mathrm{S}\).

    Prohodíme meze a tím se zbavíme mínusu před \(\mathrm{d}r\): \[t =\int_{R_\mathrm{Z}+R_\mathrm{S}}^{R_\mathrm{ZS}}{ \frac{\mathrm{d}r}{\sqrt{2\kappa M_\mathrm{S}}\sqrt{ \frac{1}{r} - \frac{1}{R_\mathrm{ZS}}}}}.\]

    Vytkneme konstantu \(\frac{1}{\sqrt{2\kappa M_\mathrm{S}}}\) před integrál: \[t =\frac{1}{\sqrt{2\kappa M_\mathrm{S}}}\int_{R_\mathrm{Z}+R_\mathrm{S}}^{R_\mathrm{ZS}}{ \frac{\mathrm{d}r}{\sqrt{ \frac{1}{r} - \frac{1}{R_\mathrm{ZS}}}}}.\]

    V integrálu členy pod odmocninou převedeme na společného jmenovatele a zlomek upravíme: \[t =\frac{1}{\sqrt{2\kappa M_\mathrm{S}}}\int_{R_\mathrm{Z}+R_\mathrm{S}}^{R_\mathrm{ZS}}{\sqrt{\frac{rR_\mathrm{ZS}}{R_\mathrm{ZS}-r}}}\mathrm{d}r.\]

    Vytkneme konstantu \(\sqrt{R_\mathrm{ZS}}\) před integrál: \[t =\sqrt{\frac{R_\mathrm{ZS}}{2\kappa M_\mathrm{S}}}\int_{R_\mathrm{Z}+R_\mathrm{S}}^{R_\mathrm{ZS}}{\sqrt{\frac{r}{R_\mathrm{ZS}-r}}}\mathrm{d}r.\tag{6}\]

     

    Řešení integrálu \(\int{\sqrt{\frac{r}{R_\mathrm{ZS}-r}}}\mathrm{d}r\)

     

    Dle http://www.wolframalpha.com/ platí: \[\int{\sqrt{\frac{r}{R_\mathrm{ZS}-r}}}\mathrm{d}r=\frac {\sqrt{\frac{r}{R_\mathrm{ZS}-r}} \left(\sqrt{r} \left(r-R_\mathrm{ZS} \right) + R_\mathrm{ZS}\sqrt{R_\mathrm{ZS}-r}  \mathrm{arctg}\,{\sqrt{\frac{r}{R_\mathrm{ZS}-r}}} \right) }{\sqrt {r}}+c,\] kde \(c\) je konstanta.

    Využitím derivace ověříme, zda to platí: \[{\sqrt{\frac{r}{R_\mathrm{ZS}-r}}}=\frac{\mathrm{d}}{\mathrm{d}r}\left(\frac {\sqrt{\frac{r}{R_\mathrm{ZS}-r}} \left(\sqrt{r} \left(r-R_\mathrm{ZS} \right) + R_\mathrm{RZ}\sqrt{R_\mathrm{ZS}-r}  \mathrm{arctg}\,{\sqrt{\frac{r}{R_\mathrm{RZ}-r}}} \right) }{\sqrt {r}}+c\right).\]

    Protože \(\frac{\mathrm{d}c}{\mathrm{d}r}=0\) dostáváme: \[{\sqrt{\frac{r}{R_\mathrm{ZS}-r}}}=\frac{\mathrm{d}}{\mathrm{d}r}\left(\frac {\sqrt{\frac{r}{R_\mathrm{ZS}-r}} \left(\sqrt{r} \left(r-R_\mathrm{ZS} \right) + R_\mathrm{ZS}\sqrt{R_\mathrm{ZS}-r}  \mathrm{arctg}\,{\sqrt{\frac{r}{R_\mathrm{ZS}-r}}} \right) }{\sqrt {r}}\right).\]

    Označíme levou stranu rovnice \(L\) a pravou stranu rovnice \(P\): \[L={\sqrt{\frac{r}{R_\mathrm{ZS}-r}}},\] \[P=\frac{\mathrm{d}}{\mathrm{d}r}\left(\frac {\sqrt{\frac{r}{R_\mathrm{ZS}-r}} \left(\sqrt{r} \left(r-R_\mathrm{ZS} \right) + R_\mathrm{ZS}\sqrt{R_\mathrm{ZS}-r}  \mathrm{arctg}\,{\sqrt{\frac{r}{R_\mathrm{ZS}-r}}} \right) }{\sqrt {r}}\right).\]

    Pravou stranu rovnice upravíme: \[P=\frac{\mathrm{d}}{\mathrm{d}r}\left( -\sqrt{r\left(R_\mathrm{ZS}-r\right)}+R_\mathrm{ZS} \mathrm{arctg}\,{\sqrt{\frac{r}{R_\mathrm{ZS}-r}}}\right).\]

    Zderivujeme závorku: \[P=-\frac{R_\mathrm{ZS}-2r}{2\sqrt{r\left(R_\mathrm{ZS}-r\right)}}+R_\mathrm{ZS}\frac{1}{1+\frac{r}{R_\mathrm{ZS}-r}}\cdot \frac{\frac{R_\mathrm{ZS}-r-r\left(-1\right)}{\left(R_\mathrm{ZS}-r \right)^2}}{2\sqrt{\frac{r}{R_\mathrm{ZS}-r}}}.\]

    Upravujeme výrazy: \[P=\frac{2r-R_\mathrm{ZS}}{2\sqrt{r}\sqrt{R_\mathrm{ZS}-r}} +R_\mathrm{ZS}\frac{1}{\frac{R_\mathrm{ZS}-r+r}{R_\mathrm{ZS}-r}}\cdot \frac{R_\mathrm{ZS}\sqrt{R_\mathrm{ZS}-r}}{2\sqrt{r}\left(R_\mathrm{ZS}-r \right)^2},\] \[P=\frac{2r-R_\mathrm{ZS}}{2\sqrt{r}\sqrt{R_\mathrm{ZS}-r}} +\left(R_\mathrm{ZS}-r\right)\cdot \frac{R_\mathrm{ZS}\sqrt{R_\mathrm{ZS}-r}}{2\sqrt{r}\left(R_\mathrm{ZS}-r \right)^2},\] \[P=\frac{2r-R_\mathrm{ZS}}{2\sqrt{r}\sqrt{R_\mathrm{ZS}-r}} + \frac{R_\mathrm{ZS}}{2\sqrt{r}\sqrt{R_\mathrm{ZS}-r}}=\frac{2r}{2\sqrt{r}\sqrt{R_\mathrm{ZS}-r}},\] \[P=\frac{\sqrt{r}}{\sqrt{R_\mathrm{ZS}-r}}=\sqrt{\frac{r}{R_\mathrm{ZS}-r}}.\]

    Tedy \[L=P.\]

     

    Výpočet \(t\)

     

    Ověřili jsme, že platí \[\int{\sqrt{\frac{r}{R_\mathrm{ZS}-r}}}\mathrm{d}r= -\sqrt{r\left(R_\mathrm{ZS}-r\right)}+R_\mathrm{ZS} \mathrm{arctg}\,{\sqrt{\frac{r}{R_\mathrm{ZS}-r}}}+c.\] Dosadíme za integrál do vztahu (6): \[t =\sqrt{\frac{R_\mathrm{ZS}}{2\kappa M_\mathrm{S}}} \left[-\sqrt{r\left(R_\mathrm{ZS}-r\right)}+R_\mathrm{ZS} \mathrm{arctg}\,{\sqrt{\frac{r}{R_\mathrm{ZS}-r}}}\right]_{R_\mathrm{Z}+R_\mathrm{S}}^{R_\mathrm{ZS}}.\] Dosadíme meze za \(r\): \(t =\sqrt{\frac{R_\mathrm{ZS}}{2\kappa M_\mathrm{S}}} \left(-\sqrt{R_\mathrm{ZS}\left(R_\mathrm{ZS}-R_\mathrm{ZS}\right)}+R_\mathrm{ZS} \lim_{r \to {R_\mathrm{ZS}}}\mathrm{arctg}\,{\sqrt{\frac{R_\mathrm{ZS}}{R_\mathrm{ZS}-r}}}\right) \) \( -\sqrt{\frac{R_\mathrm{ZS}}{2\kappa M_\mathrm{S}}}\left(-\sqrt{\left(R_\mathrm{Z}+R_\mathrm{S}\right)\left(R_\mathrm{ZS}-\left(R_\mathrm{Z}+R_\mathrm{S}\right)\right)}+R_\mathrm{ZS} \mathrm{arctg}\,{\sqrt{\frac{R_\mathrm{Z}+R_\mathrm{S}}{R_\mathrm{ZS}-\left(R_\mathrm{Z}+R_\mathrm{S}\right)}}}\right) . \)

    Platí \(\lim_{r \to {R_\mathrm{ZS}}}\mathrm{arctg}\,{\sqrt{\frac{R_\mathrm{ZS}}{R_\mathrm{ZS}-r}}}= \frac{\pi}{2}\), \(\left(R_\mathrm{ZS}-R_\mathrm{ZS}\right)=0\), \(\left(R_\mathrm{ZS}-\left(R_\mathrm{Z}+R_\mathrm{S}\right)\right)=\left(R_\mathrm{ZS}-R_\mathrm{Z}-R_\mathrm{S}\right)\) a \(\sqrt{\frac{R_\mathrm{ZS}}{2\kappa M_\mathrm{S}}}\) můžeme vytknout. Dostáváme tedy:

    \(t =\sqrt{\frac{R_\mathrm{ZS}}{2\kappa M_\mathrm{S}}} \left(R_\mathrm{ZS}\frac{\pi}{2}+\sqrt{\left(R_\mathrm{Z}+R_\mathrm{S}\right)\left(R_\mathrm{ZS}-R_\mathrm{Z}-R_\mathrm{S}\right)}-R_\mathrm{ZS} \mathrm{arctg}\,{\sqrt{\frac{R_\mathrm{Z}+R_\mathrm{S}}{R_\mathrm{ZS}-R_\mathrm{Z}-R_\mathrm{S}}}}\right). \)

    Číselné řešení:

    V tabulkách dohledáme \(\kappa\), \(R_\mathrm{Z}\), \(R_\mathrm{S}\), \(R_\mathrm{ZS}\), \(M_\mathrm{S}\) a \(\pi\):

    Gravitační konstanta: \(\kappa \dot= 6{,}67\cdot{10}^{-11} \mathrm{\frac{m^3}{kg\cdot s^2}}\).

    Poloměr Země: \(R_\mathrm{Z} \dot= 63{,}78\cdot{10}^{5} \mathrm{m}\).

    Poloměr Slunce: \(R_\mathrm{S} \dot= 6{,}96\cdot{10}^{8} \mathrm{m}\).

    Vzdálenost Země od Slunce \(R_\mathrm{ZS} \dot= 1{,}50\cdot{10}^{11} \mathrm{m}\).

    Hmotnost Slunce \(M_\mathrm{S} \dot= 1{,}99\cdot{10}^{30} \mathrm{kg}\).

    Ludolfovo číslo \(\pi \dot= 3{,}14\).

    Dosadíme: \(t  \dot= 23{,}77{\cdot} 10^{-6} \left(23{,}55{\cdot} 10^{10}+10{,}24{\cdot} 10^{9}-1{,}5{\cdot} 10^{11} \mathrm{arctg}\,{0{,}0686} \right) \mathrm{s}  \dot=  5{,}6{\cdot} 10^{6}   \mathrm{s}. \)

    Převedeme-li a výsledek zaokrouhlíme na celé dny, dostáváme: \[ t \dot= 65 \mathrm{d}.\]

  • Odpověď

    Země by padala ke Slunci dobu: \(t =\sqrt{\frac{R_\mathrm{ZS}}{2\kappa M_\mathrm{S}}} \left(R_\mathrm{ZS}\frac{\pi}{2}+\sqrt{\left(R_\mathrm{Z}+R_\mathrm{S}\right)\left(R_\mathrm{ZS}-R_\mathrm{Z}-R_\mathrm{S}\right)}-R_\mathrm{ZS}\mathrm{arctg}\,{\sqrt{\frac{R_\mathrm{Z}+R_\mathrm{S}}{R_\mathrm{ZS}-R_\mathrm{Z}-R_\mathrm{S}}}}\right). \)

    Číselně: \(t  \dot=  5{,}6{\cdot} 10^{6}  \mathrm{s}. \)

    Převedeme-li a výsledek zaokrouhlíme na celé dny, dostáváme: \[ t \dot= 65 \mathrm{d}.\]

  • Rozbor SŠ řešení

    Úlohu lze řešit i středoškolsky pomocí Keplerových zákonů. Představíme si, že Země se ke Slunci přibližuje po velmi úzké elipse. Při zužování elipsy se ohniska posouvají po hlavní poloose k hlavním vrcholům elipsy. Slunce tak leží v ohnisku takové elipsy. K řešení pak využijeme 3. Keplerův zákon.

  • SŠŘ nápověda 1

    Do jednoho obrázku nakreslete Slunce, Zemi, trajektorii Země, která neztratila svou oběžnou rychlost, a trajektorii Země, která ztratila svou oběžnou rychlost. Trajektorii Země, která ztratila svou oběžnou rychlost, zakreslete jako úzkou elipsu. V obrázku vyznačte délku hlavních poloos trajektorií.

  • SŠŘ nápověda 2

    Formulujte třetí Keplerův zákon.

  • SŠŘ nápověda 3

    Napište třetí Keplerův zákon pro případ Země, která neztratila a která ztratila svou oběžnou rychlost. Vyjádřete odtud hledanou dobu pádu \(t\).

  • Celkové řešení SŠŘ

    Obrázek znázorňující trajektorii Země, která neztratila svou oběžnou rychlost, a trajektorii Země, která ztratila svou oběžnou rychlost.

     

    trajektorie

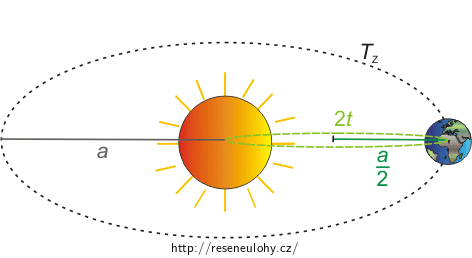
    \(T_\mathrm{Z}\) je doba oběhu Země, která neztratila svou oběžnou rychlost, a \(a\) je hlavní poloosa této trajektorie.

    \(2t\) je doba oběhu Země, která ztratila svou oběžnou rychlost, a \(\frac{a}{2}\) je hlavní poloosa této trajektorie.

     

    Třetí Keplerův zákon

     

    Poměr druhých mocnin oběžných dob dvou planet se rovná poměru třetích mocnin délek hlavních poloos jejich trajektorií.

     

    Výpočet \(t\)

     

    Dle obrázku (trajektorie) a třetího Keplerova zákona dostáváme: \[\frac{\left(2t\right)^2}{T_\mathrm{Z}^2}=\frac{\left(\frac{a}{2}\right)^3}{a^3}.\]

    Na pravé straně vykrátíme \(a\) a umocníme \(\frac{1}{2}\): \[\frac{\left(2t\right)^2}{T_\mathrm{Z}^2}=\frac{1}{8}.\]

    Obě strany rovnice vynásobíme \(\frac{T_\mathrm{Z}^2}{4}\): \[t^2=\frac{1}{8}\frac{T_\mathrm{Z}^2}{4}.\]

    Obě strany rovnice odmocníme a dostáváme: \[t=\sqrt{\frac{1}{8}}\frac{T_\mathrm{Z}}{2}.\]

    Číselné řešení:

    V tabulkách dohledáme \(T_\mathrm{Z}=365{,}26 \mathrm{d}\) a dosadíme: \[t=\sqrt{\frac{1}{8}}\frac{365{,}26}{2} \mathrm{d}  \dot= 65 \mathrm{d}.\]

  • Odpověď SŠŘ

    Země by padala ke Slunci dobu \(t=\sqrt{\frac{1}{8}}\frac{T_{Z}}{2}\).

    Číselně: \(t  \dot= 65 \mathrm{d}.\)

Úroveň náročnosti: Vysokoškolská úloha
K řešení úlohy je třeba vyhledat nějaké údaje.
Původní zdroj: Upraveno podle: Nahodil J.: Sbírka úloh z fyziky kolem nás pro střední školy. Zpracováno v bakalářské práci Michaely Jungové (2013).
×Původní zdroj: Upraveno podle: Nahodil J.: Sbírka úloh z fyziky kolem nás pro střední školy. Zpracováno v bakalářské práci Michaely Jungové (2013).
En translation
Zaslat komentář k úloze