Stoupající auto
Úloha číslo: 216
Auto o hmotnosti 1200 kg má motor o výkonu 33 kW. V jakém největším stoupání je schopno udržet rychlost 72 km·h−1?
Zápis
m = 1200 kg hmotnost auta P = 33 kW výkon motoru v = 72 km·h−1 rychlost auta α = ? (°) sklon kopce Doporučení
Než se do příkladu pustíte, pročtěte si řešení úlohy Nákladní auto a kopec.
Rozbor
Známe maximální výkon motoru auta a rychlost, kterou se auto pohybuje. Odtud můžeme zjistit maximální tažnou sílu motoru auta. Z podmínky, která musí platit pro výslednici sil působících na auto, pak spočítáme příslušný úhel stoupání.
Alternativní možností je vyjádřit si, o kolik se zvýší potenciální energie auta za určitý čas. Tento přírůstek potenciální energie je pak roven práci, kterou vykoná za tuto dobu motor auta při uvedeném výkonu.
Nápověda 1
Jaké síly na auto během pohybu působí? Jaký mají směr? Nakreslete si obrázek.
Nápověda 2
Co platí podle 1. Newtonova zákona pro výslednici těchto sil, jede-li auto stálou rychlostí?
Nápověda 3
Rozložte tíhovou sílu \(\vec{F}_\mathrm{G}\) na složku rovnoběžnou s vozovkou a na složku kolmou k vozovce. Dává 1. Newtonův zákon nějaké podmínky pro tyto složky?
Nápověda 4
Umíte vyjádřit velikost složky F0 z tíhové síly? Použijte vhodnou goniometrickou funkci.
Nápověda 5
Zbývá nám vyjádřit tažnou sílu motoru Fm. Máme zadaný výkon automobilu a jeho rychlost. Umíte z těchto údajů sílu Fm vyjádřit?
Nápověda 6
Pomocí vztahů (4), (7), (8) vyjádřete úhel α.
Celkové řešení
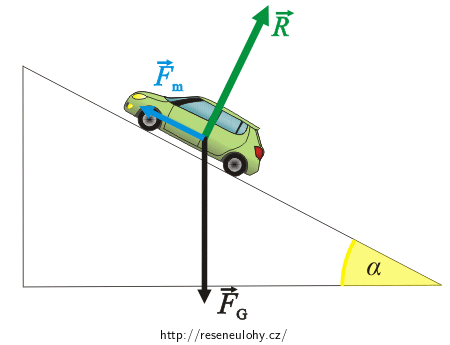
Na auto působí celkem tři síly (odpor vzduchu neuvažujeme):
1) Tíhová síla \(\vec{F}_\mathrm{G}\) působí svisle dolů.
2) Reakční síla vozovky \(\vec{R}\) (auto tlačí do vozovky a podle 3. Newtonova zákona tlačí vozovka do auta). Tato síla působí kolmo na vozovku.
3) Tahová síla motoru \(\vec{F}_\mathrm{m}\), která působí ve směru pohybu. (Reálně touto silou působí vozovka na kola auta.)
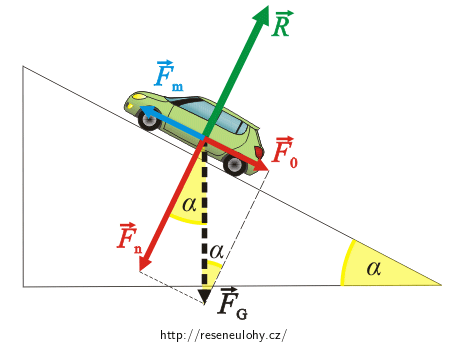
Protože se automobil pohybuje rovnoměrně přímočaře, musí být výslednice tří výše zmíněných sil nulová (nulový vektor):
\[\vec{F}_\mathrm{G} \,+\,\vec{R}\,+\,\vec{F}_\mathrm{m}\,=\,\vec{o}.\]Rozklad tíhové síly \(\vec{F}_\mathrm{G}\) na síly \(\vec{F}_0\) a \(\vec{F}_\mathrm{n}\) ukazuje obrázek:
Z něj je také patrné, že má-li být výslednice všech sil působících na automobil nulová, musí být nulové také výslednice ve směru rovnoběžném s vozovkou a ve směru kolmém k vozovce. Musí tedy platit:
\[\vec{F}_\mathrm{n}\,+\,\vec{R}\,=\,\vec{o},\tag{1}\] \[\vec{F}_0\,+\,\vec{F}_\mathrm{m}\,=\,\vec{o}.\tag{2}\]Protože síly \(\vec{F}_\mathrm{n}\) a \(\vec{R}\) mají opačný směr a síly \(\vec{F}_0\) a \(\vec{F}_\mathrm{m}\) mají také opačný směr, lze pro velikosti těchto sil psát:
\[F_\mathrm{n}\,-\,R\,=\,0,\tag{3}\] \[F_0\,-\,F_\mathrm{m}\,=\,0.\tag{4}\]Pro další výpočet nám postačí pracovat s rovnicí (4).
Z geometrie úlohy (viz obrázek výše) je patrné, že platí:
\[\sin{\alpha}\,=\,\frac{F_0}{F_\mathrm{G}}.\]Tedy:
\[F_0\,=\,F_\mathrm{G}\sin{\alpha}.\tag{5}\]Tíhovou sílu FG můžeme pomocí hmotnosti automobilu vyjádřit jako:
\[F_\mathrm{G}\,=\,mg\,,\tag{6}\]kde g je tíhové zrychlení. Dosazením vztahu (6) do vztahu (5) dostáváme:
\[F_0\,=\,mg\sin{\alpha}.\tag{7}\]Zbývá určit velikost síly \(\vec{F}_\mathrm{m}\). Vyjdeme ze vztahu \(P\,=\,F_\mathrm{m}v\), který platí pro tzv. okamžitý výkon, tedy pro okamžité hodnoty síly i rychlosti. Zřejmě nás tedy bude zajímat okamžitá velikost síly Fm při špičkovém výkonu P a rychlosti v, kterou lze vyjádřit jako:
\[F_\mathrm{m}\,=\,\frac{P}{v}.\tag{8}\]Dosadíme vztahy (7) a (8) do rovnice (4):
\[F_0\,-\,F_\mathrm{m}\,=\,0,\] \[mg\sin{\alpha}\,-\,\frac{P}{v}\,=\,0\,\Rightarrow\,sin{\alpha}\,=\,\frac{P}{mgv}.\]Číselně:
\[P\,=\,33\,\mathrm{kW}\,=\,33000\,\mathrm{W},\] \[m\,=\,1200\,\mathrm{kg},\] \[g\,=\,9{,}81\,\mathrm{m{\cdot}s^{-2}},\] \[v\,=\,72\,\mathrm{km{\cdot}h^{-1}}\,=\,20\,\mathrm{m{\cdot}s^{-1}},\] \[\sin{\alpha}\,=\,\frac{P}{mgv}\,=\,\frac{33000}{1200{\cdot}9{,}81{\cdot}20}\,\dot{=}\,0{,}140\,\Rightarrow\,\alpha\,\dot{=}\,8^{\circ}3^{\prime}.\]Kopec tedy může stoupat maximálně pod úhlem přibližně \(8^{\circ}3^{\prime}\), což představuje stoupání asi \(14{,}1\,\%\). (Stoupáním se rozumí hodnota tangenty úhlu přepočtená na procenta.)
Alternativní řešení
Za čas t ujede auto dráhu s = v·t, vystoupí tedy do výšky h = vt sin α. Jeho potenciální energie se zvýší o ΔEp:
\[{\Delta}E_\mathrm{p}\,=\,mgh\,=\,mgvt\sin{\alpha}.\]Toto zvýšení energie se rovná práci, kterou za čas t vykonal motor:
\[ W\,=\,Pt.\]Platí tedy:
\[\Delta E_\mathrm{p}\,=\,W\hspace{10px} \Rightarrow \hspace{10px}mgvt\,\sin\alpha\,=\,Pt.\]Odtud:
\[\sin\alpha\,=\,\frac{P}{mgv}\,,\]což je vztah, který jsme dostali v našem prvním řešení.
Výsledek
\[\sin{\alpha}\,=\,\frac{P}{mgv}\,=\,0{,}140\,\Rightarrow\,\alpha\,\dot{=}\,8^{\circ}3^{\prime}\]Kopec může stoupat maximálně pod úhlem přibližně \(8^{\circ}3^{\prime}\), což představuje stoupání asi \(14{,}1\,\%\).



