Brusný kotouč
Úloha číslo: 116
Brusný kotouč o poloměru R se roztáčí z klidu s konstantním úhlovým zrychlením ε okolo vodorovné osy x v kladném smyslu. V čase 0 s se bod B ležící na jeho okraji nachází v poloze B0 = [0, R] nad osou.
a) Určete závislost polohového vektoru \(\vec{r}\left(t\right)\) bodu B a jeho rychlosti \(\vec{v}\left(t\right)\) a zrychlení \(\vec{a}\left(t\right)\) na čase.
b) Určete závislost tečného zrychlení \(\vec{a}_\mathrm{t}\left(t\right)\) bodu B na čase.
c) Určete závislost normálového zrychlení \(\vec{a}_\mathrm{n}\left(t\right)\) bodu B na čase.
d) Určete úhel, který svírá celkové a normálové zrychlení bodu B.
Nápověda 1 pro a): Obrázek situace
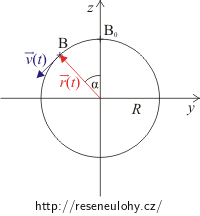
Nakreslete si obrázek, vyznačte počáteční polohu bodu B0 a polohu bodu B za okamžik t. Vyznačte i úhel α, o který se bod B za čas t pootočil. Zapište souřadnice bodu B v čase t s pomocí poloměru kola a úhlu α.
Nápověda 2 pro a): Úhlová rychlost otáčení kotouče
Kotouč se roztáčí s konstantním úhlovým zrychlením ε. Jak se mění s časem úhlová rychlost ω a jak úhel α?
Nápověda 3 pro a): Polohový vektor bodu B
Víte, jak se mění s časem souřadnice bodu B. Zapište s jejich pomocí jeho polohový vektor.
Nápověda 4 pro a): Rychlost bodu B
Jak od souřadnice x(t) a y(t) přejdete ke složkám rychlosti vx(t) a vy(t)? S jejich pomocí pak zapište vektor rychlosti \(\vec{v}\left(t\right)\).
Nápověda 5 pro a): Celkové zrychlení bodu B
Obdobně jako jste došli od souřadnic ke složkám rychlosti, přejděte od složek rychlosti ke složkám celkového zrychlení. Pomocí složek pak zapište vektor zrychlení.
Nápověda 6 pro b): Tečné zrychlení
Spočítejte nejprve velikost tečného zrychlení.
Jakým směrem míří tečné zrychlení?
Jak zapíšete jednotkový vektor ve směru rychlosti?
Znáte-li velikost tečného zrychlení a jednotkový vektor v jeho směru, zapíšete již snadno vektor tečného zrychlení.
Nápověda 7 pro c): Normálové zrychlení
Spočítejte nejprve velikost normálového zrychlení.
Jakým směrem míří normálové zrychlení?
Jak zapíšete jednotkový vektor ve směru polohového vektoru?
Znáte-li velikost normálového zrychlení a jednotkový vektor v jeho směru, zapíšete již snadno vektor normálového zrychlení.
Nápověda 8 pro d): Úhel mezi celkovým a normálovým zrychlením
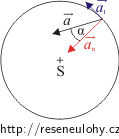
Nakreslete obrázek, ve kterém vyznačíte normálové, celkové a tečné zrychlení a hledaný úhel. Jaká goniometrická funkce je spojuje, jistě snadno objevíte.
K výpočtu budete potřebovat ještě velikost celkového zrychlení. Pomůže vám buď znalost at a an, nebo ay a az.
CELKOVÉ ŘEŠENÍ
a) Polohový vektor bodu B
Nakreslíme obrázek situace.
Obrázek 1:
Souřadnice bodu B:
\[y\,=\,-R\,\sin\alpha,\] \[z\,=\,R\,\cos\alpha.\]Výpočet velikosti úhlové rychlosti ω a úhlu α:
\[\varepsilon\,=\,\mathrm{konst.}\,,\] \[\omega\,=\,\int{\varepsilon}\,\mathrm{d}t\,=\,\varepsilon{t}+C\,.\]Konstantu C určíme z počátečních podmínek.
Pro t = 0 je \(\omega \,=\,0\), a tedy:
\[0\,=\,0+C\,.\]Odtud C = 0:
\[\omega \,=\, \varepsilon t\,.\]Pro úhel α platí:
\[\alpha\,=\,\int{\omega}\,\mathrm{d}t\,=\, \int{\left(\varepsilon t\right)\mathrm{d}t} \,=\, \frac{1}{2}\varepsilon{t^{2}}+K\,.\]Konstantu K určíme z počátečních podmínek.
Pro t = 0 je α = 0, a tedy:
\[0\,=\,0+K\,.\]Odtud K = 0:
\[ \alpha\,=\,\frac{1}{2}\varepsilon{t^{2}}\,.\tag{1}\]Polohový vektor bodu B:
\[\vec{r}\left(t\right)\,=\, y\vec{j}+ z\vec{k}\,,\]kde \(\vec{j}\), \(\vec{k}\) jsou jednotkové vektory ve směru souřadnicových os y a z:
\[\vec{r}\left(t\right)\,=\,-R\,\sin\alpha\vec{j}+ R\,\cos\alpha\vec{k}\,.\]Dosadíme za α ze vztahu (1):
\[\vec{r}\left(t\right)\,=\,-R\,\sin\frac{\varepsilon{t^{2}}}{2}\vec{j}+R\,\cos\frac{\varepsilon{t^{2}}}{2}\vec{k}\,.\tag{2}\]a) Rychlost bodu B
Pro průběh rychlosti bodu B na obvodu kotouče platí:
\[\vec{v}\left(t\right)\,=\,\frac{\mathrm{d}\vec{r}\left(t\right)}{\mathrm{d}t}\,=\,\frac{\mathrm{d}y\left(t\right)}{\mathrm{d}t}\vec{j}+\frac{\mathrm{d}z\left(t\right)}{\mathrm{d}t}\vec{k}\,,\] \[v_\mathrm{y}\,=\,\frac{\mathrm{d}y\left(t\right)}{\mathrm{d}t}\,=\, \frac{\mathrm{d}}{\mathrm{d}t}\left(-R\,\sin\frac{\varepsilon{t^{2}}}{2}\right)\,=\, -R\varepsilon{t}\,\cos\frac{\varepsilon{t^{2}}}{2}\,,\] \[v_\mathrm{z}\,=\,\frac{\mathrm{d}z\left(t\right)}{\mathrm{d}t}\,=\, \frac{\mathrm{d}}{\mathrm{d}t}(R\,\cos\frac{\varepsilon{t^{2}}}{2})\,=\, -R\varepsilon{t}\,\sin\frac{\varepsilon{t^{2}}}{2}\,,\] \[\vec{v}\left(t\right)\,=\, v_\mathrm{y}\left(t\right)\vec{j}+ v_\mathrm{z}\left(t\right)\vec{k}\,,\] \[\vec{v}\left(t\right)\,=\,-R\varepsilon{t}\,\cos\frac{\varepsilon{t^{2}}}{2}\vec{j}-R\varepsilon{t}\,\sin\frac{\varepsilon{t^{2}}}{2}\vec{k}\,,\tag{3}\]kde \(\vec{j}\), \(\vec{k}\) jsou jednotkové vektory ve směru souřadnicových os.
Pro velikost rychlosti platí:
\[ v\left(t\right)\,=\,\sqrt{v_\mathrm{y}^{2}+v_\mathrm{z}^{2}}\,=\,R\varepsilon t\sqrt{\cos^{2}{\frac{\varepsilon t^2}{2}} + \sin^{2}{\frac{\varepsilon t^2}{2}}}\,=\, R\varepsilon t\,.\tag{4}\]a) Zrychlení bodu B
Průběh zrychlení:
\[\vec{a}\left(t\right)\,=\,\frac{\mathrm{d}\vec{v}\left(t\right)}{\mathrm{d}t} \,=\,\frac{\mathrm{d}v_\mathrm{y}\left(t\right)}{\mathrm{d}t}\vec{j}+\frac{\mathrm{d}v_\mathrm{z}\left(t\right)}{\mathrm{d}t}\vec{k}\,,\] \[a_\mathrm{y}\,=\,\frac{\mathrm{d}v_\mathrm{y}\left(t\right)}{\mathrm{d}t}\,=\, \frac{\mathrm{d}}{\mathrm{d}t}\left(-R\varepsilon t\,\cos\frac{\varepsilon{t^{2}}}{2}\right)\,,\] \[a_\mathrm{y}\,=\, -R\varepsilon\,\cos\frac{\varepsilon{t^{2}}}{2}+R\varepsilon^{2}t^{2}\,\sin\frac{\varepsilon{t^{2}}}{2}\,,\] \[a_\mathrm{z}\,=\,\frac{\mathrm{d}v_\mathrm{z}\left(t\right)}{\mathrm{d}t} \,=\, \frac{\mathrm{d}}{\mathrm{d}t}(-R\varepsilon{t}\,\sin\frac{\varepsilon{t^{2}}}{2})\,,\] \[a_\mathrm{z}\,=\, -R\varepsilon\,\sin\frac{\varepsilon{t^{2}}}{2}-R\varepsilon^{2}t^{2}\,\cos\frac{\varepsilon{t^{2}}}{2}\,,\] \[\vec{a}\left(t\right)\,=\, a_\mathrm{y}\left(t\right)\vec{\,j\,}+ a_\mathrm{z}\left(t\right)\vec{\,k\,}\,,\]\[\vec{a}\left(t\right)=\left(R\varepsilon^{2}t^{2}\,\sin\frac{\varepsilon{t^{2}}}{2}-R\varepsilon\cos\frac{\varepsilon{t^{2}}}{2}\right)\vec{j}-\left(R\varepsilon\sin\frac{\varepsilon{t^{2}}}{2}+R\varepsilon^{2}t^{2}\,\cos\frac{\varepsilon{t^{2}}}{2}\right)\vec{k}\,,\]
kde \(\vec{j}\), \(\vec{k}\) jsou jednotkové vektory ve směru souřadnicových os.
b) Tečné zrychlení bodu B
Velikost tečného zrychlení:
\[a_t\left(t\right)\,=\,\frac{\mathrm{d}v\left(t\right)}{\mathrm{d}t}\,=\,\frac{\mathrm{d}}{\mathrm{d}t}\left(R\varepsilon{t}\right)\,=\,R\varepsilon\,.\]Tečné zrychlení má směr rychlosti:
\[\vec{a}_\mathrm{t}\,=\,a_\mathrm{t}\vec{v}_\mathrm{ok}\,. \]kde \(\vec{v}_\mathrm{ok} \) je jednotkový vektor ve směru rychlosti.
Jednotkový vektor získáme, když vektor vydělíme jeho velikostí, tedy:
\[\vec{v}_\mathrm{ok}\,=\,\frac{\vec{v}}{v}\,.\]Podílem vztahu (3) a (4) dostaneme:
\[\vec{v}_\mathrm{ok} \,=\,\frac{\vec{v}}{v} \,=\, -\cos\frac{\varepsilon{t^{2}}}{2}\vec{j}-\sin\frac{\varepsilon{t^{2}}}{2}\vec{k}\,,\]kde \(\vec{j}\), \(\vec{k}\) jsou jednotkové vektory ve směru souřadnicových os.
Tečné zrychlení je pak rovno:
\[\vec{a}_\mathrm{t}\left(t\right)\,=\, a_\mathrm{t}\vec{v}_\mathrm{ok} \,=\, -R\varepsilon\,\cos\frac{\varepsilon{t^{2}}}{2}\vec{\,j\,}-R\varepsilon\,\sin\frac{\varepsilon{t^{2}}}{2}\vec{\,k\,}\,.\]c) Normálové zrychlení bodu B
Velikost normálového zrychlení:
\[a_\mathrm{n}\,=\,\frac{v^{2}}{R}\,=\,\frac{R^{2}\varepsilon^{2}t^{2}}{R}\,=\,R\varepsilon^{2}t^{2}\,.\]Normálové zrychlení má směr polohového vektoru, ale je opačně orientované:
\[\vec{a}_\mathrm{n}\left(t\right)\,=\, a_\mathrm{n} \left(- \vec{r}_o\right)\,,\]kde \(\vec{r}_0\) je jednotkový vektor ve směru polohového vektoru.
Jednotkový vektor získáme, když vektor vydělíme jeho velikostí, tedy:
\[\vec{r}_0\,=\,\frac{\vec{r}}{r}\,.\]Vydělením vztahu (2) poloměrem R dostaneme:
\[\vec{r}_0 \,=\,\frac{\vec{r}}{r} \,=\, -\sin\frac{\varepsilon{t^{2}}}{2}\vec{j}+\cos\frac{\varepsilon{t^{2}}}{2}\vec{k}\,,\]kde \(\vec{j}\), \(\vec{k}\) jsou jednotkové vektory ve směru souřadnicových os.
Normálové zrychlení je pak rovno:
\[\vec{a}_\mathrm{n}\left(t\right)\,=\, a_\mathrm{n} \left(- \vec{r}_0\right)\,=\, R\varepsilon^{2}t^{2}\,\sin\frac{\varepsilon{t^{2}}}{2}\vec{j}- R\varepsilon^{2}t^{2}\,\cos\frac{\varepsilon{t^{2}}}{2}\vec{k}\,.\]Poznámka: Tečné a normálové zrychlení jsou na sebe kolmá. Jednotkový vektor ve směru normálového zrychlení lze také získat tak, že napíšeme vektor kolmý na jednotkový vektor ve směru tečného zrychlení.
d) Úhel α, který svírá celkové a normálové zrychlení
Obrázek 2:
Pro úhel α platí:
\[\cos\alpha\,=\,\frac{a_\mathrm{n}}{a}\,.\tag{5}\]Výpočet velikosti celkového zrychlení a:
\[a\,=\,\sqrt{a_\mathrm{t}^{2}+a_\mathrm{n}^{2}} \,=\,\sqrt{\left(R\varepsilon\right)^{2}+ \left(R\varepsilon^{2}t^{2}\right)^{2}}\,=\, R\varepsilon\sqrt{1+\varepsilon^{2}t^{4}}\,.\]Dosadíme do (5):
\[\cos\alpha\,=\,\frac{a_\mathrm{n}}{a}\,=\,\frac{R\varepsilon^{2}t^{2}}{R\varepsilon\sqrt{1+\varepsilon^{2}t^{4}}}\,=\,\left(1+\frac{1}{\varepsilon^{2}t^{4}}\right)^{-\frac{1}{2}}\,.\]Odpověď
a) Polohový vektor bodu B:
\[\vec{r}(t)\,=\,-R\,\sin\frac{\varepsilon{t^{2}}}{2}\vec{j}+R\,\cos\frac{\varepsilon{t^{2}}}{2}\vec{k}\,. \]Průběh rychlosti bodu B:\[\vec{v}\left(t\right)\,=\,-R\varepsilon{t}\,\cos\frac{\varepsilon{t^{2}}}{2}\vec{j}-R\varepsilon{t}\,\sin\frac{\varepsilon{t^{2}}}{2}\vec{k}\,.\]Průběh zrychlení bodu B:\[\vec{a}\left(t\right)=\left(R\varepsilon^{2}t^{2}\sin\frac{\varepsilon{t^{2}}}{2}-R\varepsilon\cos\frac{\varepsilon{t^{2}}}{2}\right)\vec{j}-\left(R\varepsilon\,\sin\frac{\varepsilon{t^{2}}}{2}+R\varepsilon^{2}t^{2}\,\cos\frac{\varepsilon{t^{2}}}{2}\right)\vec{k}\,,\]
kde \(\vec{j}\), \(\vec{k}\) jsou jednotkové vektory ve směru souřadnicových os.
b) Tečné zrychlení:
\[\vec{a}_\mathrm{t}\left(t\right)\,=\,-R\varepsilon\,\cos\frac{\varepsilon{t^{2}}}{2}\vec{j}-R\varepsilon\,\sin\frac{\varepsilon{t^{2}}}{2}\vec{\,k\,}\,,\]kde \(\vec{\,j\,}\), \(\vec{k}\) jsou jednotkové vektory ve směru souřadnicových os.
c) Normálové zrychlení:
\[\vec{a}_\mathrm{n}\left(t\right)\,=\,\varepsilon^{2}Rt^{2}\,\sin\frac{\varepsilon{t^{2}}}{2}\vec{j}- \varepsilon^{2}Rt^{2}\,\cos\frac{\varepsilon{t^{2}}}{2}\vec{k}\,,\]kde \(\vec{j}\), \(\vec{k}\) jsou jednotkové vektory ve směru souřadnicových os.
d) Úhel α, který svírá celkové a normálové zrychlení:
\[\cos\alpha\,=\,\frac{a_\mathrm{n}}{a}\,=\,\frac{R\varepsilon^{2}t^{2}}{R\varepsilon\sqrt{1+\varepsilon^{2}t^{4}}}\,=\,\left(1+\frac{1}{\varepsilon^{2}t^{4}}\right)^{-\frac{1}{2}}\,.\]