Volně padající kámen
Úloha číslo: 126
Volně padající kámen má v jednom bodě své dráhy okamžitou rychlost 5 m·s−1 a v jiném, níže položeném bodě má rychlost 8 m·s−1. Za jaký čas doletí kámen z prvního bodu do druhého a jak daleko jsou oba dva body od sebe vzdálené?
Zápis
v1 = 5 m·s−1 rychlost kamenu v jednom bodě v2 = 8 m·s−1 rychlost kamenu v níže položeném bodě t = ? (s) čas, za který kámen doletí z prvního bodu do druhého s = ? (m) vzdálenost bodů Z tabulek: g = 9,81 m·s−2 tíhové zrychlení Nápověda 1: Čas doletu tělesa z prvního bodu do druhého
Jakým pohybem se kámen pohybuje? Připomeňte si, jaký vztah platí mezi velikostí rychlosti a dobou tohoto pohybu.
Jak vyjádříte čas doletu kamene z jednoho bodu své dráhy do druhého? Znáte všechny veličiny, které k výpočtu potřebujete?
Nápověda 2: Vzdálenost bodů
Víte, že se kámen pohyboval volným pádem. Jak zjistíte vzdálenost dvou bodů, kterými proletěl neboli dráhu, kterou uletěl z prvního bodu do druhého?
Při výpočtu využijte vztahy (1), (2) z minulé nápovědy.
CELKOVÉ ŘEŠENÍ
Čas letu z bodu 1 do bodu 2
Kámen se pohybuje rovnoměrně zrychleným pohybem.
Pro závislost rychlosti volného pádu na čase platí: \(v(t) \,=\, gt.\)
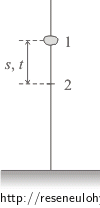
Čas t, za který se přemístí kámen z jednoho bodu do druhého, se rovná rozdílu časů, ve kterých byl kámen v bodě 2 a v bodě 1 (viz obrázek), tedy:
\[t\,=\,t_2\,-\,t_1.\]Ze zadání víme, že se jedná o volný pád. Rychlost v bodě 1 je rovna
\[v_1 \,=\, gt_1\,.\]Odtud:
\[t_1 \,=\, \frac{v_1}{g}\,.\tag{1}\]Rychlost v bodě 2 je rovna
\[v_2 \,=\, gt_2\,.\]Odtud:
\[t_2 \,=\, \frac{v_2}{g}\,.\tag{2}\]Pro čas t dostaneme:
\[t\,=\,\frac{v_2}{g}\,-\,\frac{v_1}{g}\,=\,\frac{v_2\,-\,v_1}{g}\,.\]Číselně:
\[t\,=\,\frac{8\,-\,5}{9{,}81}\,\mathrm{s}\,\dot=\,0{,}3\,\mathrm{s}\,.\]Vzdálenost bodů 1 a 2
Pro závislost dráhy volného pádu na čase platí:
\[s \,=\, \frac{1}{2}\,gt^{2}\,.\]Vzdálenost bodů 1 a 2 určíme jako rozdíl dráhy, kterou kámen urazil do bodu 2, a dráhy, kterou urazil do bodu 1:
\[s\,=\,s_2\,-\,s_1\,=\,\frac{gt_2^{2}}{2}\,-\,\frac{gt_1^{2}}{2}\,=\,\frac{g}{2}\,\left(t_2^{2}\,-\,t_1^{2}\right).\]Za t2 a t1 dosadíme ze vztahů (1) a (2):
\[s\,=\,\frac{g}{2}\,\left(\frac{v_2^{2}}{g^{2}}\,-\,\frac{v_1^{2}}{g^{2}}\right)\,=\,\frac{1}{2g}(v_2^{2}\,-\,v_1^{2}).\]Číselně:
\[s\,=\,\frac{1}{2{\cdot} 9{,}81}\cdot(8^{2}-5^{2})\,\mathrm{m}\,\dot=\,2\,\mathrm{m}\,.\]Odpověď
Kámen doletí z prvního do druhého bodu za čas
\[t\,=\,\frac{v_2\,-\,v_1}{g}\,\dot=\,0{,}3\,\mathrm{s}\,.\]Vzdálenost dvou bodů, kterými kámen proletěl, je
\[s\,=\,\frac{1}{2g}(v_2^{2}\,-\,v_1^{2})\,\dot=\,2\,\mathrm{m}\,.\]





