Stěhování nákladu
Úloha číslo: 2266
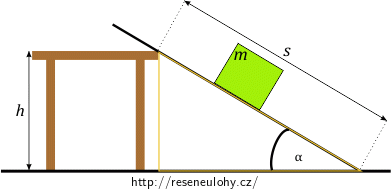
Náklad o hmotnosti \(20\,\mathrm{kg}\) přesunujeme konstantní rychlostí ze stolu vysokého \(1{,}2\,\mathrm{m}\) po nakloněném prkně po dráze \(2{,}4\,\mathrm{m}\) na podlahu. Koeficient tření je \(0{,}5\).
a) Je nutné náklad tlačit dolů nebo přidržovat zpět? Jak velkou silou?
b) Nechť je nyní náklad přesouván z podlahy na stůl působením síly \(200\,\mathrm{N}\) rovnoběžné s prknem. Jakou rychlost, kinetickou energii a potenciální energii bude mít náklad na horním konci prkna?
c) Jak velká je práce vykonaná třecí silou?
Zápis a rozbor
\(m=20\,\mathrm{kg}\)…hmotnost nákladu
\(s=2{,}4\,\mathrm{m}\)…délka prkna
\(h=1{,}2\,\mathrm{m}\)…výška stolu
\(f=0{,}5\)…koeficient tření
\(\vec {v_0}= konst.\) …přesun konstantní rychlostí
\(F_1=200\,\mathrm{N}\)…síla, kterou posouváme bednu
Obrázek situace:
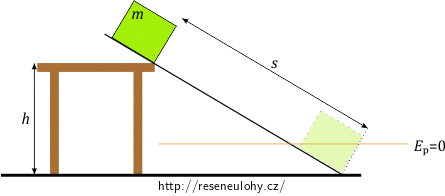
Bedna je umístěna na nakloněné rovině (prkně). Působí na ni tedy několik sil, které budou ovlivňovat její pohyb. Pokud je bedna v klidu nebo v rovnoměrném přímočarém pohybu, je výslednice všech sil, které na bednu působí, nulová.
Působí-li na bednu nenulová výsledná síla, udává jí zrychlení podle druhého Newtonova zákona. Bedna se pohybuje rovnoměrně zrychleným/zpomaleným pohybem.
Abychom mohli určit potenciální energii, musíme zvolit její nulovou hladinu. Nechť prochází těžištěm bedny v situaci, kdy se dotkla podlahy (viz obr.). Kinetická energie závisí na rychlosti, která se v případě rovnoměrně zrychleného pohybu s rostoucí uraženou drahou zvyšuje.
Práci konáme, jestliže působíme silou po dráze. Pozor, působí-li síla kolmo ke směru pohybu, práci nekonáme!
Nápověda a)
Rozmyslete si, jaké všechny síly na bednu působí a zda mají vliv na její pohyb po prkně. Chceme-li, aby se bedna pohybovala konstantní rychlostí, co to znamená pro výslednici sil?
Nápověda b)
Působí-li na bednu nenulová výslednice sil, co můžeme říct o typu jejího pohybu? Co platí pro dráhu a rychlost takového pohybu?
Nápověda c)
Třecí síla je po dobu pohybu konstantní a působí rovnoběžně se směrem posunu bedny. Jakým způsobem budeme v takovém případě počítat práci?
Řešení a)
Na bednu působí tíhová síla \(\vec {F_\mathrm{G}}\) v těžišti, třecí síla \(\vec{F_\mathrm{t}}\) mezi bednou a podložkou proti směru pohybu bedny, tlaková síla podložky \(\vec N\) (kolmá na podložku). Nakreslíme si obrázek a do něj vyznačíme síly:
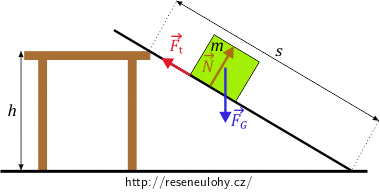
Bednu máme po nakloněné rovině posunovat konstantní rychlostí. To znamená, že rychlost bedny se nemění, a její pohyb je tedy rovnoměrný. Předpokládáme, že prkno je rovné a bedna se pohybuje po přímce - pohyb je přímočarý.
Rovnoměrný přímočarý pohyb nastane pouze tehdy, je-li výslednice sil působících na bednu nulová. Rozdělíme síly na rovnoběžné s prknem a kolmé k prknu. Vidíme, že tíhovou sílu nemůžeme hned do jedné z těchto skupin zařadit, proto ji do požadovaných směrů rozložíme. Rozklad uděláme pomocí doplnění na rovnoběžník. Složky tíhové síly v daných směrech označíme \(F_\mathrm{Gx}\) a \(F_\mathrm{Gy}\).
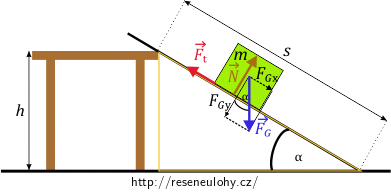
Věnujme se nejprve silám, které jsou kolmé k prknu. Jejich výslednice je nulová, protože se bedna v tomto směru nepohybuje. Velikosti sil \(F_\mathrm{Gy}\) a \(N\), působících v opačných směrech, musí být tedy stejné:
\[F_\mathrm{Gy}=N.\tag{1}\]
Zda bude bednu potřeba tlačit, nebo brzdit poznáme podle výslednice sil rovnoběžných s prknem. Vypočteme velikosti sil \({F_\mathrm{t}}\) a \(F_\mathrm{Gx}\). Bude-li větší třecí síla, musíme bednu tlačit, v opačném případě ji musíme brzdit.
Pro velikost třecí síly platí:
\[F_\mathrm{t} = Nf,\]
kde \(N\) je obecně síla kolmá k podložce. Podle (1) můžeme psát
\[F_\mathrm{t}=F_\mathrm{Gy}f.\tag{2}\]
Z obrázku 2 a podobnosti trojúhelníků vidíme, že úhel \(\alpha\) svírají \(F_\mathrm{Gy}\) s \(F_\mathrm{G}\). Velikost úhlu \(\alpha\) jsme odvodili v poznámce.
S využitím goniometrických funkcí vyjádříme:
\[F_\mathrm{Gy}=F_\mathrm{G} \cos{\alpha},\tag{3}\]
\[F_\mathrm{Gx}=F_\mathrm{G} \sin{\alpha}.\tag{4}\]
Dosazením do (2) z (3) a použitím (4) dostáváme:
\[F_\mathrm{t}=fF_\mathrm{G} \cos{\alpha}=fmg\cos{\alpha},\]
\[F_\mathrm{Gx}=F_\mathrm{G} \sin{\alpha}=mg\sin{\alpha}.\]
Dosadíme hodnoty a vypočteme:
\[F_\mathrm{t}=0{,}5 {\cdot} 20 \cdot 10\cdot \cos{30^{\circ}} \,\mathrm{N}=100\cdot \frac{\sqrt 3}{2} \,\mathrm{N}=\sqrt 3 {\cdot} 50 \,\mathrm{N} \doteq 86{,}6 \,\mathrm N,\]
\[F_\mathrm{Gx}=20 {\cdot} 10 \cdot \sin{30^{\circ}}\,\mathrm N = 200 \cdot \frac{1}{2} \,\mathrm{N}=100 \,\mathrm{N}.\]
Dospěli jsme tedy k výsledku. Složka tíhové síly rovnoběžná s prknem je větší než třecí síla. Bedna se bude pohybovat zrychleně dolů, proto je třeba ji brzdit.
Brzdit ji musíme tak velkou silou, aby byla výslednice sil nulová. Tedy:
\[F_\mathrm{b} = F_\mathrm{Gx} - F_\mathrm{t} = (100 - 86{,}6)\,\mathrm N = 13{,}4\,\mathrm N.\]
Řešení b)
Označme sílu, kterou je bedna posunována, jako \(\vec{F_1}\). Touto silou tlačíme bednu rovnoběžně s deskou. Abychom dokázali určit rychlost \(\vec v\), potenciální energii \(E_\mathrm{p}\) a kinetickou energii \(E_\mathrm{k}\) na horním konci prkna, potřebujeme určit výslednou sílu, která na bednu působí. Zakresleme si všechny síly působící na bednu do obrázku.
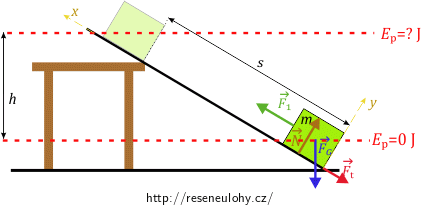
Podle druhého Newtonova zákona platí:
\[\vec{F_\mathrm{G}} + \vec {F_{1}} + \vec {F_\mathrm{t}}+\vec{N}=m\vec{a}.\]
Zvolme souřadný systém podle obrázku a rozepišme silové rovnice skalárně po složkách:
\[x: F_1-F_\mathrm{G_{x}}-F_\mathrm{t}=ma,\]
\[y: N-F_\mathrm{G_{y}}=0.\]
Složky tíhové síly umíme vyjádřit pomocí úhlu sklonu \(\alpha\) nakloněné roviny (viz poznámka) a třecí sílu počítáme opět podle vztahu (2). Po úpravě dostaneme:
\[x: F_1 -mg\sin{\alpha}-Nf=ma,\]
\[y: N=mg\cos{\alpha}.\]
Nyní můžeme dosadit z druhé rovnice do první za \(N\) a vyjádřit zrychlení:
\[a=\frac{F_1 -mg\sin {\alpha}-fmg\cos {\alpha}}{m},\tag{6}\]
\[a = \frac{200 - 20 {\cdot} 10 \cdot \sin {30^{\circ}}-0{,}5{\cdot} 20 \cdot 10 \cdot \cos {30^{\circ}}}{20} = \frac{200 - 200 {\cdot} 0{,}5-0{,}5{\cdot} 200 \cdot \frac{\sqrt{3}}{2}}{20} \,\dot=\, 0{,}7\,\mathrm{m \cdot s^{-2}}. \]
Chceme určit rychlost na druhém konci prkna. To znamená, že bedna urazí dráhu \(s\). Bedna na této dráze rovnoměrně zrychluje. Rychlost a dráhu rovnoměrně zrychleného pohybu umíme zapsat:
\[s = \frac{1}{2}at^2,\tag{7}\]
\[ v = a t,\tag{8}\]
kde \(t\) je čas, za který bedna dráhu urazí.
Budeme-li uvažovat velikosti zmíněných veličin, můžeme ze soustavy rovnic (6), (7), (8) vyjádřit a spočítat hledanou rychlost \(v\).
Z rovnice (8) vyjádříme čas \(t\) a dosadíme do rovnice (7). Vyjádříme hledanou rychlost \(v\), přičemž zrychlení \(a\) máme již určené z rovnice (6).
Nejprve obecně:
\[t =\frac{v}{a}, \]
\[s = \frac{a}{2} \frac{v^2}{a^2}=\frac{v^2}{2a},\]
\[v =\sqrt{2sa}.\]
Nyní dosadíme \(a = 0{,}7\,\mathrm {m \cdot s^{-2}}\), \(s = 2{,}4\,\mathrm m\), \(m = 20\,\mathrm {kg}\):
\[v = \sqrt{2{\cdot} 2{,}4 {\cdot} 0{,}7} \,\mathrm{m\cdot s^{-1}}\,\dot=\,1{,}8\,\mathrm{m\cdot s^{-1}}.\]
Pro kinetickou energii \(E_\mathrm{k}\) obecně platí:
\[E_\mathrm{k}=\frac{1}{2}mv^2.\]
Rychlost v místě, kde chceme kinetickou energii určit, jsme již spočetli. Stačí pouze dosadit. Dostaneme:
\[E_\mathrm{k} \,\dot=\, \frac{1}{2}\cdot 20 \cdot {1{,}8}^2 \,\mathrm{J}= 10{\cdot} 3{,}24 \,\mathrm{J}= 32{,}4\,\mathrm{J}.\]
Zbývá určit potenciální energii. Podle obrázku (viz obr. 4) je zřejmé, že těleso zvedneme do výšky stolu \(h\). Potenciální energii určíme podle vztahu:
\[E_\mathrm{p} = mgh,\]
\[E_\mathrm{p} = 20{\cdot} 10\cdot 1{,}2\,\mathrm{J} = 240\,\mathrm{J}.\]
Řešení c)
Třecí síla působí ve směru pohybu, práci můžeme počítat podle vztahu:
\[W = F_\mathrm{t} s.\]
Velikost třecí síly jsme určili v řešení části a).
Dostaneme:
\[W=sfmg\cos{\alpha},\]
\[W=86{,}6{\cdot} 2{,}4 \,\mathrm J \,\dot=\, 207{,}8\,\mathrm J.\]
Odpověď a)
Bednu je třeba přidržovat zpět silou o velikosti 13,4 N.
Odpověď b)
Náklad bude mít na horním konci prkna rychlost \(v\,\dot=\,1{,}8\,\mathrm {m\cdot s^{-1}}\), kinetickou energii \(E_\mathrm{k}\,\dot=\,32{,}4\,\mathrm{J}\) a potenciální energii \(E_\mathrm{p} = 240\,\mathrm{J}\).
Odpověď c)
Práce, kterou vykoná třecí síla, je \(W\,\dot=\,207{,}8\,\mathrm J\).