Chlapec na kladce
Úloha číslo: 142
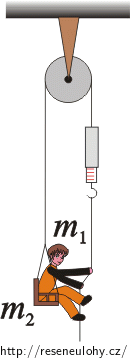
Na pevné kladce je zavěšeno lano, na jehož jednom konci je ocelová sedačka o hmotnosti 32 kg a na druhém konci siloměr. Chlapec o hmotnosti 64 kg sedící na zavěšené sedačce táhne za siloměr tak, že ukazuje 600 N.
a) Vypočtěte velikost zrychlení, s jakým se chlapec a sedačka pohybují a určete, zda je za daných podmínek zrychlení obou těles namířeno vzhůru či dolů.
b) Určete velikost síly, kterou působí chlapec na sedačku.
Hmotnost kladky a lana neuvažujte.
Zápis
m2 = 32 kg hmotnost sedačky m1 = 64 kg hmotnost chlapce 600 N údaj na siloměru a = ? m·s−2 zrychlení, s jakým se chlapec a sedačka pohybují N2 = ? N velikost síly, kterou působí chlapec na sedačku Nápověda 1 – pohybové rovnice (výpočet zrychlení)
Uvědomte si, jaké síly působí na chlapce a na sedačku. Nakreslete si obrázek a síly v něm vyznačte. Napište pohybové rovnice pro chlapce a sedačku.
Doporučení: Pro přehlednost si nakreslete síly působící na chlapce a sedačku zvlášt do dvou obrázků.
Nápověda 2 – pohybové rovnice skalárně, vztahy mezi tahovými silami a tlakovými silami
Zvolte si vhodně soustavu souřadnic a přepište pohybové rovnice skalárně. Uvědomte si, jaký je vztah mezi tlakovou silou, kterou působí sedačka na chlapce, a tlakovou silou, kterou působí chlapec na sedačku. Podobně se zamyslete nad tahovými silami.
Nápověda 3 – výpočet zrychlení
Sečtěte rovnice (5) a (6) a vyjádřete zrychlení.
Nápověda 4 – velikost tlakové síly
Velikost tlakové síly, kterou působí chlapec na sedačku, můžete vyjádřit z rovnice (6) a dosadit za zrychlení.
CELKOVÉ ŘEŠENÍ
Nejprve nakreslíme do obrázku všechny síly působící na chlapce a na sedačku a napíšeme pro ně pohybové rovnice.
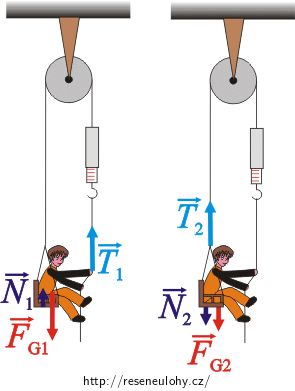
Na chlapce působí následující síly:
\(\vec{N}_1\)…tlaková síla, kterou sedačka působí na chlapce,
\(\vec{T}_1\)…tahová síla, kterou lano působí na chlapce,
\(\vec{F}_\mathrm{G_1}\)…tíhová síla, kterou Země působí na chlapce.
Na sedačku působí následující síly:
\(\vec{N}_2\)…tlaková síla, kterou chlapec působí na sedačku,
\(\vec{T}_2\)…tahová síla, kterou lano působí na sedačku,
\(\vec{F}_\mathrm{G_2}\)…tíhová síla, kterou Země působí na sedačku.
Pohybová rovnice pro chlapce:
\[\vec{T}_1+\vec{N}_1+\vec{F}_\mathrm{G_1}\,=\, m_1\vec{a}.\tag{1}\]Pohybová rovnice pro sedačku:
\[\vec{T}_2+\vec{N}_2+\vec{F}_\mathrm{G_2}\,=\, m_2\vec{a}.\tag{2}\]Abychom mohli pohybové rovnice přepsat skalárně, zvolíme si vhodně soustavu souřadnic. Osu y volíme ve směru pohybu chlapce i sedačky a orientujeme ji směrem vzhůru.
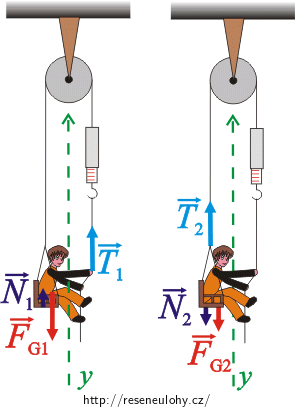
Pohybová rovnice skalárně pro chlapce:
\[T_1+N_1-F_\mathrm{G_1}\,=\, m_1a.\tag{3}\]Pohybová rovnice skalárně pro sedačku:
\[T_2-N_2-F_\mathrm{G_2}\,=\, m_2a.\tag{4}\]Jelikož hmotnost kladky zanedbáváme, nemá žádný moment setrvačnosti a neovlivňuje tah lana. Pro velikosti tahových sil lana podle 3. Newtonova zákona platí:
\[|\vec{T}_1|\,=\,|\vec{T}_2|.\]Tlaková síla, kterou působí chlapec na sedačku, je podle 3. Newtonova zákona stejně velká jako síla, kterou působí sedačka na chlapce:
\[|\vec{N}_1|\,=\,|\vec{N}_2|.\]Přepíšeme rovnice (3) a (4):
\[T_2+N_2-F_\mathrm{G_1}\,=\, m_1a,\tag{5}\] \[T_2-N_2-F_\mathrm{G_2}\,=\, m_2a.\tag{6}\]Výpočet velikosti zrychlení a:
Rovnice (5) a (6) sečteme:
\[2T_2-F_\mathrm{G_2}-F_\mathrm{G_1}\,=\,(m_2+m_1)a.\]Vyjádříme zrychlení:
\[a\,=\,\frac{2T_2-F_\mathrm{G_2}-F_\mathrm{G_1}}{m_2+m_1},\] \[a\,=\,\frac{2T_2-m_2g-m_1g}{m_2+m_1},\] \[a\,=\,\frac{2T_2}{m_2+m_1}-\frac{m_2g+m_1g}{m_2+m_1}\,=\, \frac{2T_2}{m_2+m_1}-g.\tag{7}\]Do vztahu (7) dosadíme číselně:
\[a\,=\,\left(\frac{2\,\cdot\,600}{32\,+\,64}\,-\,9{,}81\right)\,\mathrm{m\cdot s^{-2}} \,=\,\left(\frac{1\,200}{96}\,-\,9{,}81\right)\,\mathrm{m\cdot s^{-2}},\] \[a \,=\,(12{,}5\,-\,9{,}81)\,\mathrm{m\cdot s^{-2}}\,=\,2{,}69\,\mathrm{m\cdot s^{-2}}.\]Poznámka: Velikost zrychlení vyšla kladně. Chlapec se sedačkou se tedy pohybují vzhůru ve směru osy y. V případě, že bychom zvolili směr osy y dolů, vyšlo by zrychlení záporné. Z této skutečnosti bychom mohli usoudit, že směr zrychlení je opačný.
Výpočet velikosti tlakové síly N2:
Z rovnice (6) vyjádříme N2:
\[N_2\,=\,T_2-F_\mathrm{G_2}-m_2a,\] \[N_2\,=\,T_2-m_2g-m_2a.\]Dosadíme za zrychlení ze vztahu (7):
\[N_2\,=\,T_2-m_2g-m_2\left(\frac{2T_2}{m_2+m_1}\,-\,g\right),\] \[N_2\,=\,T_2-\frac{2T_2m_2}{m_2+m_1},\] \[N_2\,=\,\frac{T_2m_1+T_2m_2-2T_2m_2}{m_2+m_1},\] \[N_2\,=\,T_2\left(\frac{m_1-m_2}{m_2+m_1}\right).\tag{8}\]Do vztahu (8) dosadíme číselně:
\[N_2\,=\,600\,\left(\frac{64\,-\,32}{32\,+\,64}\right)\,\mathrm{N}\,=\,\frac{600 {\cdot} 32}{96}\,\mathrm{N}\,=\,\frac{600}{3}\,\mathrm{N}\,=\,200\,\mathrm{N}.\]Celková odpověď
Zrychlení, s jakým se chlapec a sedačka pohybují, je \[a \,=\, \frac{2T_2}{m_2+m_1}\,-\,g \,=\, 2{,}69\,\mathrm{m\cdot s^{-2}}.\]
Zrychlení je za daných podmínek orientováno vzhůru.
Velikost síly, kterou působí chlapec na sedačku, je \[N_2 \,=\, T_2\,\left(\frac{m_1-m_2}{m_2+m_1}\right)\,=\,200\,\mathrm{N}.\]






