Dvojice závaží na kladce
Úloha číslo: 529
Přes kladku je vedeno vlákno, na jehož koncích visí závaží o hmotnostech m1 a m2 (m2 > m1). Předpokládejme, že vlákno je nehmotné a kladka homogenní válec o poloměru r a hmotnosti m3. Určete zrychlení závaží.
Zápis
m1 hmotnost prvního závaží m2 hmotnost druhého závaží m3 hmotnost kladky r poloměr kladky a = ? zrychlení závaží Moment setrvačnosti válce
Podle tabulek je moment setrvačnosti válce při otáčení podle osy symetrie \(J=\frac{1}{2}mr^2\).
Rozbor
Úlohu je možné řešit dvěma způsoby. Buď pomocí zákona zachování mechanické energie (A), nebo přes impulsové věty (B). V prvním případě je třeba zvolit dvě vhodné situace, ve kterých budete mechanickou energii kladky a obou závaží srovnávat.
Při řešení přes impulsové věty je třeba uvážit, které všechny síly působí na jednotlivá závaží a kladku a co platí pro jejich výslednici. Pro otáčející se kladku je třeba napsat i druhou větu impulsovou.
(Impulsové věty viz úloha Kutálející se obruč.)
Nápověda 1A
Vyberte dvě situace, ve kterých budete mechanickou energii obou závaží a kladky srovnávat. Nezapomeňte zvolit hladinu nulové potenciální energie.
Nápověda 2A
Vyjádřete si jednotlivé energie (potenciální a kinetickou) obou závaží a kladky v situaci 1 a 2. Dosaďte do vztahu (1).Zapeklitá otázka 3A
Ve vztazích pro kinetickou energii figuruje rychlost. Vyjádřete ji pomocí zrychlení a uražené dráhy h.
Nápověda 1B
Nakreslete do obrázku všechny síly, které působí na obě závaží a kladku.
Nápověda 2B
Napište, co platí pro výslednice sil působící na jednotlivá závaží i kladku. Pro kladku napište i druhou větu impulsovou.
Nápověda 3B
Z rovnic (3), (4), (5) vyjádřete hledané zrychlení.
Celkové řešení pomocí zákona zachování mechanické energie
Vybereme dvě situace, ve kterých budeme mechanickou energii obou závaží a kladky srovnávat. Zvolíme hladinu nulové potenciální energie.
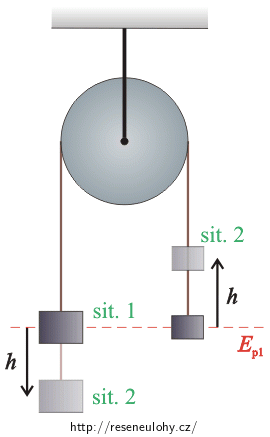
V první situaci nastavíme závaží, aby těžiště byla ve stejné výšce, a tu použijeme jako nulovou hladinu potenciální energie.
Porovnáme mechanické energie Ep1, Ek1 obou závaží a kladky na počátku (sit. 1) a po uražení dráhy h: Ep2, Ek2 (sit. 2).
Podle zákona zachování mechanické energie platí:
\[E_\mathrm{p1}+E_\mathrm{k1} = E_\mathrm{p2}+E_\mathrm{k2}\,.\tag{1}\]Jelikož se soustava na počátku nehýbe, je
\[E_\mathrm{k1}=0.\]Potenciální energie obou závaží je rovněž nulová. Jediná část soustavy, která z nulové hladiny vyčnívá, je kladka. Její potenciální energii označíme Epkladky:
\[E_\mathrm{p1}=E_\mathrm{pkladky}.\]Potenciální energie těžšího závaží ubývá, v situaci 2 je rovna -m2gh, naopak u lehčího závaží přibývá a v situaci 2 je rovna m1gh. Potenciální energie kladky se nemění. Celková potenciální energie soustavy v situaci 2 je rovna:
\[E_\mathrm{p2}=(m_1-m_2)gh+E_\mathrm{pkladky}\,.\]Kinetická energie závaží je rovna součtu kinetických energií obou závaží \(E_\mathrm{kz}=\frac{1}{2}m_1v^2+\frac{1}{2}m_2v^2=\frac{1}{2}(m_1+m_2)v^2\) a kinetické energie otáčení kladky \(E_\mathrm{ot}=\frac{1}{2}J\omega^2\).
Obvodová rychlost kladky je rovna rychlosti pohybu závaží, proto \(\omega=\frac{v}{r}\).
Moment setrvačnosti kladky \(J=\frac{1}{2}m_3r^2\).
Dosadíme:
\[E_\mathrm{ot}=\frac{1}{2}(\frac{1}{2}m_3r^2)(\frac{v}{r})^2=\frac{1}{4}m_3v^2.\]Celková kinetická energie soustavy v situaci 2 je rovna:
\[E_\mathrm{k2} = \frac{1}{2}(m_1+m_2)v^2 + \frac{1}{4}m_3v^2\,.\]Dosazením do vztahu (1) dostaneme:
\[E_\mathrm{pkladky} = (m_1-m_2)gh+E_\mathrm{pkladky} + \frac{1}{2}(m_1+m_2)v^2 + \frac{1}{4}m_3v^2\,.\]Upravíme:
\[(m_2-m_1)gh = \frac{1}{2}(m_1+m_2 + \frac{1}{2}m_3)v^2\,.\tag{2}\]Ve vztazích pro kinetickou energii figuruje rychlost. Vyjádříme ji pomocí zrychlení a uražené dráhy h.
Závaží se pohybují rovnoměrně zrychleným pohybem. Pro uraženou dráhu h platí:
\[h=\frac{1}{2}at^2\,.\]Pro rychlost platí:
\[v=at\,.\]Pak:
\[h=\frac{v^2}{2a}\,.\]Odtud:
\[v^2 = 2ah\,.\]Dosadíme do (2):
\[(m_2-m_1)gh = \frac{1}{2}(m_1+m_2 + \frac{1}{2}m_3)2ah\,.\]Zkrátíme h:
\[(m_2-m_1)g = (m_1+m_2 + \frac{1}{2}m_3)a\,.\]Vyjádříme a:
\[a=\frac{(m_2-m_1)g}{m_1+m_2+\frac{1}{2}m_3}\,.\]Celkové řešení pomocí impulsových vět
Do obrázku nakreslíme všechny síly, které působí na obě závaží a kladku.
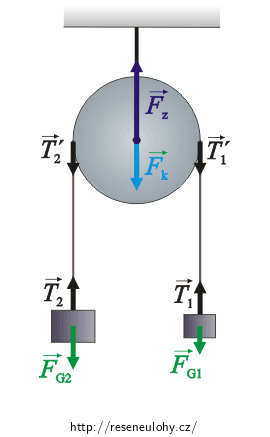
Na závaží působí tíhové síly \(\vec{F}_\mathrm{G1}\), \(\vec{F}_\mathrm{G2}\) a tahy vlákna \(\vec{T_1}\), \(\vec{T_2}\) které podle 3. Newtonova zákona působí stejně velkou, opačně orientovanou silou \(\vec{T_1^,}\) a \(\vec{T_2^,}\) na kladku.
Dále na kladku působí tíhová síla \(\vec{F}_\mathrm{k}\) a síla \(\vec{F}_\mathrm{z}\), kterou působí závěs kladky tak, aby kladka nespadla.
Pro výslednice sil platí:
Závaží 1:
\[\vec{F}_\mathrm{G1} + \vec{T}_1= m_1\vec{a}\,.\]Skalárně (soustava souřadná je zavedena tak, aby směr nahoru byl kladný):
\[T_1 - F_\mathrm{G1} = m_1a. \tag{3}\]Závaží 2:
\[\vec{F}_\mathrm{G2} + \vec{T}_2= m_2\vec{a}\,.\]Skalárně:
\[T_2 - F_\mathrm{G2} = -m_2a\,,\] \[- T_2 + F_\mathrm{G2} = m_2a\,.\tag{4}\]Kladka:
\[\vec{F}_\mathrm{k} + \vec{F}_\mathrm{z} + \vec{T^,}_{1}+ \vec{T^,}_{2} = 0\,.\]Skalárně:
\[-F_\mathrm{k} + F_\mathrm{z} - T_{1}^, - T_{2}^, = 0\,.\]Pro výslednici momentů sil působících na kladku vzhledem ke středu platí:
\[\vec{r} \times \vec{T^,}_{1}+ \vec{r} \times \vec{T^,}_{2} = J\vec{\epsilon}\,.\]Skalárně:
(Směr otáčení hodinových ručiček bereme jako záporný.)
\[r T_{2}^, - r T_{1}^, = J\epsilon.\]Dosadíme za \(J=\frac{1}{2}m_3r^2\), \(\epsilon = \frac{a}{r}\), \(T_{1}^,=T_{1}\), \(T_{2}^,=T_{2}\):
\[r T_{2} - r T_{1} = (\frac{1}{2}m_3r^2)\frac{a}{r},\] \[T_{2} - T_{1} = \frac{1}{2}m_3a.\tag{5}\]Z rovnic (3), (4), (5) vyjádříme hledané zrychlení:
\[T_1 - F_\mathrm{G1} = m_1a, \tag{3}\] \[- T_2 + F_\mathrm{G2} = m_2a, \tag{4}\] \[T_{2} - T_{1} = \frac{1}{2}m_3a.\tag{5}\]Součtem rovnic (3), (4) a (5) dostáváme:
\[F_\mathrm{G2}-F_\mathrm{G1}=m_1a+m_2a+\frac{1}{2}m_3a\,,\] \[a=\frac{F_\mathrm{G2}-F_\mathrm{G1}}{m_1+m_2+\frac{1}{2}m_3}\,,\] \[a=\frac{g(m_2-m_1)}{m_1+m_2+\frac{1}{2}m_3}\,.\]Odpověď
Velikost zrychlení závaží je \[a=\frac{(m_2-m_1)g}{m_1+m_2+\frac{1}{2}m_3}.\]




