Srážka aut
Úloha číslo: 745
Dvě auta jedou přímo proti sobě. První rychlostí o velikosti 20 m·s-1, druhé rychlostí o velikosti 30 m·s-1. Obě auta jsou schopna zastavit z rychlosti o velikosti 25 m·s-1 za 5 s.
a) Jak daleko musí být od sebe auta, aby se nesrazila?
b) Jak daleko by auta musela být, kdybychom započetli reakční dobu řidičů, která je rovna asi 0,2 s?
Zápis
v1 = 20 m·s−1 rychlost jízdy prvního auta v2 = 30 m·s−1 rychlost jízdy druhého auta v0 = 25 m·s−1 počáteční rychlost aut t0 = 5 s čas, za který auta zastaví z rychlosti v0 tr = 0,2 s reakční doba řidičů a) s = ? (m) vzdálenost aut b) sr = ? (m) vzdálenost aut při započtení reakční doby Nápověda 1 pro a): Grafické řešení – graf závislosti rychlosti na čase
Zkuste úlohu vyřešit nejprve graficky.
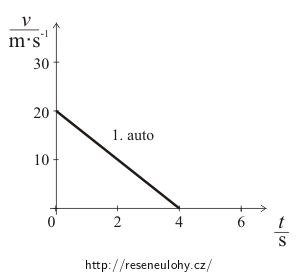
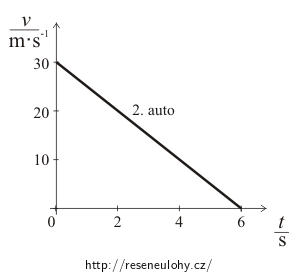
Nakreslete si grafy závislostí rychlostí obou aut na čase při jejich zastavování.
Předpokládejte, že pokles rychlosti obou aut je rovnoměrný.
Nápověda 2 pro a): Grafické řešení – dráha zastavení
Kde je v grafech z předchozí nápovědy schovaná dráha zastavení obou aut?
Nápověda 3 pro a): Početní řešení – dráhy zastavení
Nyní budeme řešit úlohu početně s využitím vztahů pro rovnoměrně zpomalený přímočarý pohyb.
Znáte velikosti rychlostí obou aut a za předpokladu, že pokles rychlosti obou aut je rovnoměrný, znáte i jejich zrychlení.
Jak vypočtete dráhy zastavení obou aut?
Nápověda 4 pro b): Reakční doba řidičů
Je třeba započítat reakční dobu řidičů.
K dráze vypočítané v bodě a) musíme tedy připočítat dráhu, kterou oba řidiči ujedou, než stačí zareagovat.
Jak ji zjistíme?
CELKOVÉ ŘEŠENÍ:
a) Grafické řešení:
Předpokládáme, že pokles rychlosti je rovnoměrný.
Velikosti rychlostí obou aut se tedy sníží za 1 s o 5 m·s-1.
První auto tak zastaví za 4 s, druhé auto zastaví za 6 s.
Obrázek 1 – Graf závislosti rychlosti prvního auta na čase:
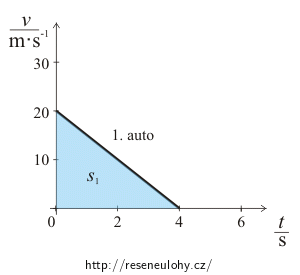
Dráha zastavení prvního auta odpovídá ploše pod křivkou prvního grafu.
Pro dráhu s1 zastavení prvního auta platí:
\[s_1=\frac{20{\cdot}4}{2}\,\mathrm{m}=40\,\mathrm{m}.\]Obrázek 2 – Graf závislosti rychlosti druhého auta na čase:
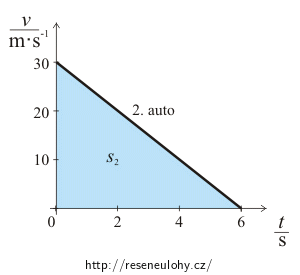
Dráha zastavení druhého auta odpovídá ploše pod křivkou druhého grafu.
Pro dráhu s2 zastavení druhého auta platí:
\[s_2=\frac{30{\cdot}6}{2}\,\mathrm{m}=90\,\mathrm{m}.\]Aby se auta nesrazila, musela by být od sebe vzdálena:
\[s=s_1+s_2 =130\,\mathrm{m}.\]a) Početní řešení:
Velikosti rychlostí aut:
\[v_1= 20\,\mathrm{m\cdot s^{-1}},\] \[v_2= 30\,\mathrm{m\cdot s^{-1}}.\]Zrychlení aut:
Obě auta jsou schopna zastavit z rychlosti 25 m·s-1 za 5 s. Za 1 s se rychlost sníží při rovnoměrném brzdění o 5 m·s-1. Velikost zrychlení aut je tedy:
\[a= \frac{v_0}{t_0} = 5\,\mathrm{m\cdot s^{-2}}.\]Výpočet dráhy zastavení:
Rychlost a dráha rovnoměrně zpomaleného přímočarého pohybu se s časem mění podle níže uvedených vztahů, známých ze střední školy:
\[v \,=\, v_\mathrm{p}-at,\tag{1}\] \[s \,=\, v_\mathrm{p}t-{\frac{1}{2}}at^2,\tag{2}\]kde vp je počáteční rychlost, ze které se začíná brzdit.
V okamžiku zastavení bude rychlost auta nulová. Ze vztahu (1) pro rychlost zjistíme čas zastavení tz. Platí:
\(0=v_\mathrm{p} - at_\mathrm{z}.\)Odtud:
\(t_\mathrm{z}\,=\,\frac{v_\mathrm{p}}{a}.\)Dráhu zastavení sz dostaneme dosazením za čas zastavení do vztahu (2):
\[s_\mathrm{z}\,=\, v_\mathrm{p}t_\mathrm{z}- {\frac{1}{2}}at_\mathrm{z}^2 \,=\,v_\mathrm{p}\left(\frac{v_\mathrm{p}}{a}\right)-{\frac{1}{2}}a\left(\frac{v_\mathrm{p}}{a}\right)^2,\] \[s_\mathrm{z}=\frac{v_\mathrm{p}^{2}}{2a}.\]Dráha zastavení prvního auta:
\[s_1=\frac{v_1^{2}}{2a},\] \[s_1=\frac{20^{2}}{2{\cdot}5}\,\mathrm{m}=40\,\mathrm{m}.\]Dráha zastavení druhého auta:
\[s_2=\frac{v_2^{2}}{2a},\] \[s_2=\frac{30^{2}}{2{\cdot}5}\,\mathrm{m}=90\,\mathrm{m}.\]Aby se auta nesrazila, musela by být od sebe vzdálena:
\[s=s_1+s_2 = \frac{v_1^{2}+v_2^{2} }{2a} = 130\,\mathrm{m}.\]b) Početní řešení se započtením reakční doby řidičů:
Vzdálenost aut (tak, aby se nesrazila) vypočítaná v bodě a):
\[s_1+s_2 =(40+90)\,\mathrm{m}=130\,\mathrm{m}.\]K tomu je třeba ještě připočítat dráhu, kterou oba řidiči ujedou, než stačí zareagovat a začnou brzdit.
Reakční dobu si označíme tr:
\[t_\mathrm{r}=0{,}2\,\mathrm{s}.\]Dráha, kterou ujede první auto, než řidič zareaguje, je:
\[s_\mathrm{r1}=v_1\cdot t_\mathrm{r}=(20{\cdot}0{,}2)\,\mathrm{m}=4\,\mathrm{m}.\]Dráha, kterou ujede druhé auto, než řidič zareaguje, je:
\[s_\mathrm{r2}=v_2\cdot t_\mathrm{r}=(30{\cdot}0{,}2)\,\mathrm{m}=6\,\mathrm{m}.\]Celková vzdálenost aut by pak musela být:
\[s_\mathrm{r}=(s_1+s_2+s_\mathrm{r1}+s_\mathrm{r2})=(40+90+6+4)\,\mathrm{m}=140\,\mathrm{m}.\]Odpověď
a) Aby se auta nesrazila, musela by být od sebe vzdálena:
\[s=s_1+s_2 = \frac{v_1^{2}+v_2^{2}}{2a} = 130\,\mathrm{m},\] \[(a = \frac{v_0}{t_0} = 5\,\mathrm{m\cdot s^{-2}}).\]b) Se započtením reakční doby řidičů by celková vzdálenost aut (aby nedošlo ke srážce) musela být:
\[s_\mathrm{r} =(s_1+s_2+s_\mathrm{r1}+s_\mathrm{r2})=(\frac{v_1^{2}+v_2^{2}}{2a} + v_1t_\mathrm{r} + v_2t_\mathrm{r})\,\mathrm{m}=140\,\mathrm{m}.\]