Sbírka řešených úloh

Intenzita gravitačního pole mezi Zemí a Měsícem

Úloha číslo: 517

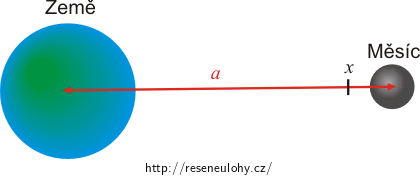
Ve kterém místě spojnice Země – Měsíc je výsledná intenzita gravitačního pole obou těles nulová? Vyjádřete pomocí hmotnosti Země, Měsíce a vzdálenosti a jejich středů.

• Teorie – intenzita gravitačního pole

  Intenzita gravitačního pole \(\vec {K}\) je vektorová veličina definovaná vztahem:

  \[\vec {K} = \frac{\vec {F}_g}{m}\,.\]

  Kde F_g je gravitační síla působící v daném místě pole na testovací objekt hmotnosti m.

  Používá se k modelování prostorových vlastností pole. Jednoduchými úpravami totiž dojdeme k tomu, že nezávisí na hmotnosti testovacího objektu:

  \[\vec {K} = -\kappa \frac{M}{r^2} \frac{\vec {r}}{r}\,.\tag{1}\]

  M je hmotnost tělesa, které tvoří centrální gravitační pole, r je vzdálenost jeho středu (resp. polohový vektor) od zkoumaného místa a κ je gravitační konstatnta.

  A naopak právě jen její znalost a znalost hmotnosti zkoumaného tělesa stačí k určení gravitační síly na tělesou působící:

  \[\vec {F}_g = m\vec {K}\,.\]

• Nápověda 1

  Hledáme místo na spojnici Země a Měsíce, kde bude výsledná intenzita gravitačního pole nulová. Nakreslete si do obrázku, kam bude směřovat vektor intenzity gravitačního pole Země a totéž pro Měsíc. Co bude platit pro jejich velikosti, pokud neuvažujeme působení ostatních vesmírných těles?

• Řešení nápovědy 1

  

  Výsledná intenzita v hledaném místě má být nulová. Platí tedy:

  \[\vec{K}_{celk.} = \vec{K}_{Zeme} + \vec{K}_{Mesic} = 0\,.\]

  Vzhledem k tomu, že hledáme místo na spojnici obou těles, pak oba polohové vektory určující směr a vzdálenost místa od Země (resp. od Měsíce) budou rovnoběžné a budou mít opačný směr.

  Vektorovou rovnici přepíšeme skalárně:

  \[K_{celk.} = K_{Zeme} - K_{Mesic} = 0\,.\]

  V místě, kde příspěvky Země a Měsíce budou stejné, pak musí platit:

  \[K_{Zeme} = K_{Mesic}\,.\]

• Nápověda 2

  Pomocí vztahu (1) vyjádřete intenzitu gravitačního pole Země a Měsíce v hledaném místě.

  Zvažte, jak vhodně zapsat vzdálenost r, aby z ní bylo možno vyjádřit polohu bodu x.

• Řešení nápovědy 2

  Víme, že platí: \(K = \kappa \frac{M}{r^2}\) a  \(K_{Zeme} = K_{Mesic}\)

  Z obrázku je zřejmé, že můžeme psát (počítáme-li x jako vzdálenost od středu Země):

  \[\kappa \frac{M}{x^2} = \kappa \frac{m}{(a-x)^2}\,,\]

  pro x z intervalu (R_Z; a − R_M).

  Odtud:

  \[\frac{M}{x^2} = \frac{m}{(a-x)^2}\,,\] \[\frac{x^2}{M} = \frac{(a-x)^2}{m}\,.\]

  Hmotnosti i vzdálenosti jsou kladné, odmocnění je tedy ekvivalentní úprava.

  \[\frac{x}{\sqrt{M}} = \frac{(a-x)}{\sqrt{m}}\]

  Odtud:

  \[x = a \frac{\sqrt{M}}{\sqrt{M}+\sqrt{m}}\,.\]

• Nápověda 3 – hodnoty z tabulek

  K číselnému řešení úlohy, budete potřebovat údaje, které nejsou zadané. Vyhledejte je v tabulkách nebo na internetu.

• Řešení nápovědy 3

  Gravitační konstanta κ ≈ 6,67 · 10^-11 m³kg^-1s^-2

  Hmotnost Země M ≈ 6 · 10²⁴ kg

  Hmotnost Měsíce m ≈ 7,3 · 10²² kg

  Vzdálenost Země – Měsíc a ≈ 384 000 km

  Číselný výpočet:

  \[x = a \frac{\sqrt{M}}{\sqrt{M}+\sqrt{m}},\] \[x = 384 000 \cdot \frac{\sqrt{6 {\cdot} 10^{24}}}{\sqrt{6 {\cdot} 10^{24}}+\sqrt{7{,}3 {\cdot} 10^{22}}}\,\mathrm{km} \approx 346 000\,\mathrm{km}.\]

• Celkové řešení

  

  Výsledná intenzita v hledaném místě má být nulová. Platí tedy:

  \[\vec{K}_{celk.} = \vec{K}_{Zeme} + \vec{K}_{Mesic} = 0\,.\]

  Vektorovou rovnici přepíšeme skalárně (viz náčrtek):

  \[K_{celk.} = K_{Zeme} - K_{Mesic} = 0\,.\]

  V místě, kde příspěvky Země a Měsíce budou stejné, pak musí platit:

  \(K_{Zeme} = K_{Mesic}\,,\)

  \(\kappa \frac{M}{x^2} = \kappa \frac{m}{(a-x)^2}\,,\)       pro x z intervalu (R_Z; a − R_M)

  \(\frac{M}{x^2} = \frac{m}{(a-x)^2}\,,\)

  \(\frac{x^2}{M} = \frac{(a-x)^2}{m}\,.\)

  Hmotnosti i vzdálenosti jsou kladné, odmocnění je tedy ekvivalentní úprava.

  \[\frac{x}{\sqrt{M}} = \frac{(a-x)}{\sqrt{m}}\]

  Odtud:

  \[x = a \frac{\sqrt{M}}{\sqrt{M}+\sqrt{m}}\,.\]

  Číselně:

  \[x = 384 000 \cdot \frac{\sqrt{6 {\cdot} 10^{24}}}{\sqrt{6 {\cdot} 10^{24}}+\sqrt{7{,}3 {\cdot} 10^{22}}} km \approx 346 000\,\mathrm{km}.\]

• Odpověď

  Intenzita gravitačního pole mezi Zemí a Měsícem je nulová v bodě x (měřeno od Země), pro který platí:

  \[x = a \frac{\sqrt{M}}{\sqrt{M}+\sqrt{m}}\,.\]

  Číselně: x ≈ 346000 km.