Práce vykonaná při přenesení náboje
Úloha číslo: 180
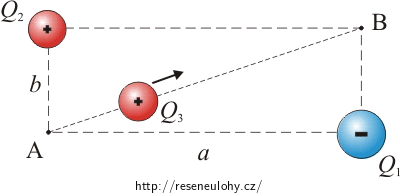
Obdélník na obrázku má strany dlouhé a = 15 cm a b = 5 cm. V protilehlých vrcholech jsou umístěny náboje Q1 = −5 µC a Q2 = +2 µC. Jakou práci vykoná elektrická síla při přenesení třetího náboje Q3 = +3 µC z vrcholu A po úhlopříčce obdélníka do vrcholu B?
Nápověda: Výpočet práce
Práce vykonaná elektrickou silou při přenesení náboje v elektrickém poli závisí na velikosti přeneseného náboje a rozdílu potenciálu v počátečním a koncovém bodě.
Nápověda: Potenciál bodového náboje
Potenciál pole bodového náboje závisí na velikosti a vzdálenosti náboje.
Rozbor
Práce vykonaná elektrickou silou při přenesení náboje v elektrickém poli je rovna rozdílu elektrické potenciální energie v počátečním a koncovém bodě. (Je to stejné jako s prací tíhové síly v tíhovém poli. Práce vykonaná tíhovou silou je rovna tomu, o kolik se zmenší tíhová potenciální energie.)
Potenciál v daném bodě je roven elektrické potenciální energii v tomto bodě vztažené na jednotkový náboj. Elektrická potenciální energie je tedy přímo úměrná elektrickému potenciálu v daném bodě a velikosti náboje umístěného v tomto bodě.
Naše pole vytváří dva bodové náboje. V takovém případě je celkový potenciál roven součtu potenciálů pole jednoho a druhého náboje.
Potenciál elektrického pole bodového náboje je přímo úměrný velikosti náboje a nepřímo úměrný vzdálenosti náboje od místa, kde potenciál zjišťujeme. Má stejné znaménko jako samotný náboj.
Abychom tedy úlohu vyřešili, určíme nejprve potenciály v bodě A a B. Z nich určíme elektrickou potenciální energii třetího náboje v těchto místech. Práce, kterou vykonají elektrické síly, je pak rovná rozdílu těchto potenciálních energii.
Výpočet potenciálu v bodě A a B
Práce vykonaná elektrickou silou na přenesení náboje v elektrickém poli je rovna rozdílu elektrické potenciální energie v počátečním bodě A a v koncovém bodě B:
\[W\,=\,E_\mathrm{pA} - E_\mathrm{pB}.\]Potenciál elektrického pole je potenciální energie vztažená na jednotkový náboj. Potenciální energii si tedy vyjádříme pomocí potenciálu Ep = Q3φ. Práci pak vypočítáme:
\[W\,=\,Q_3\left( \varphi_\mathrm{A}-\varphi_\mathrm{B}\right)\,.\]V této části řešení spočítáme potenciály pole v bodech A a B a v následující části řešení pak dopočítáme práci.
Potenciál pole vyvolaného prvním a druhým nábojem v bodě A je roven součtu potenciálů polí jednotlivých nábojů:
\[\varphi_\mathrm{A} \,=\,\varphi_\mathrm{1A} + \varphi_\mathrm{2A}\, ,\tag{1}\]kde φ1A je potenciál pole prvního náboje a φ2A potenciál pole druhého náboje v bodě A.
Analogický vztah platí pro potenciál v bodě B:
\[\varphi_\mathrm{B}\,=\,\varphi_\mathrm{1B}+\varphi_\mathrm{2B}.\tag{2}\]Pro elektrický potenciál pole bodového náboje Q ve vzdálenosti r od něj platí obecný vztah:
\[\varphi\,=\,\frac{1}{4 \pi \epsilon_0}\frac{Q}{r}\,.\]Náboj Q1 má od bodu A vzdálenost a. Potenciál pole vyvolaného prvním nábojem v bodě A je tedy:
\[\varphi_\mathrm{1A}\,=\,\frac{1}{4 \pi \epsilon_0}\frac{Q_1}{a}\,.\]Od bodu B má náboj Q1 vzdálenost b. Potenciál v bodě B je tedy:
\[\varphi_\mathrm{1B}\,=\,\frac{1}{4 \pi \epsilon_0}\frac{Q_1}{b}\,.\]Analogicky si vyjádříme potenciál pole vyvolaného druhým nábojem v bodě A
\[\varphi_\mathrm{2A}\,=\,\frac{1}{4 \pi \epsilon_0}\frac{Q_2}{b}\,,\] \[\varphi_\mathrm{2B}\,=\,\frac{1}{4 \pi \epsilon_0}\frac{Q_2}{a}\,.\]Vztahy dosadíme do vzorce (1) pro výpočet celkového potenciálu v bodě A:
\[\varphi_\mathrm{A} \,=\,\,\frac{1}{4 \pi \epsilon_0} \left(\frac{Q_1}{a} + \frac{Q_2}{b}\right).\tag{*}\]a do vzorce (2) pro výpočet celkového potenciálu v bodě B:
\[\varphi_\mathrm{B}\,=\,\frac{1}{4 \pi \epsilon_0} \left(\frac{Q_1}{b} + \frac{Q_2}{a}\right).\tag{**}\]Získali jsme celkové potenciály elektrického pole v bodech A a B.
Výpočet práce
V předchozí části řešení jsme již řekli, že práce vykonaná elektrickou silou je přímo úměrná velikosti přeneseného náboje a rozdílu potenciálu pole v počátečním a koncovém bodě:
\[W\,=\,Q_3\left( \varphi_\mathrm{A}-\varphi_\mathrm{B}\right).\tag{***}\]Potenciály v bodě A a B jsme spočítali v předchozím oddíle (Výpočet potenciálu v bodě A a B):
\[\varphi_\mathrm{A} \,=\,\,\frac{1}{4 \pi \epsilon_0} \left(\frac{Q_1}{a} + \frac{Q_2}{b}\right),\] \[\varphi_\mathrm{B}\,=\,\frac{1}{4 \pi \epsilon_0} \left(\frac{Q_1}{b} + \frac{Q_2}{a}\right).\]Nyní oba vztahy pro potenciály dosadíme do vzorce pro výpočet práce (***):
\[W\,=\,\frac{Q_3}{4 \pi \epsilon_0}\left[ \left(\frac{Q_1}{a} + \frac{Q_2}{b}\right)- \left(\frac{Q_1}{b} + \frac{Q_2}{a}\right)\right].\]Výraz budeme upravovat, abychom ho zjednodušili. Nejdříve dáme zlomky se stejným jmenovatelem k sobě:
\[W\,=\,\frac{Q_3}{4 \pi \epsilon_0}\left( \frac{Q_1}{a} + \frac{Q_2}{b}- \frac{Q_1}{b} - \frac{Q_2}{a}\right)\,=\,\frac{Q_3}{4 \pi \epsilon_0}\left( \frac{Q_1-Q_2}{a} + \frac{Q_2-Q_1}{b} \right).\]Čitatele druhého zlomku v závorce upravíme tak, aby byl stejný jako čitatel prvního zlomku a mohli jsme ho vytknout:
\[W\,=\,\frac{Q_3}{4 \pi \epsilon_0}\left( \frac{Q_1-Q_2}{a} - \frac{Q_1-Q_2}{b} \right).\]Čitatele zlomků vytkneme, a tím získáme výsledný vztah pro výpočet vykonané práce:
\[W\,=\,\frac{Q_3\left(Q_1-Q_2\right)}{4 \pi \epsilon_0}\left( \frac{1}{a} - \frac{1}{b} \right).\]Zápis a číselné dosazení
\(a\,=\,15\,\mathrm{cm}\,=\,1{,}5{\cdot}10^{-1}\,\mathrm{m}\)
\(b\,=\,5\,\mathrm{cm}\,=\,5{\cdot}10^{-2}\,\mathrm{m}\)
\(Q_1\,=\,-5\,\mathrm{\mu C}\,=\,-5{\cdot}10^{-6}\,\mathrm{ C}\)
\(Q_2\,=\,+2\,\mathrm{\mu C}\,=\,+2{\cdot}10^{-6}\,\mathrm{ C}\)
\(Q_3\,=\,+3\,\mathrm{\mu C}\,=\,+3{\cdot}10^{-6}\,\mathrm{ C}\)
\(W\,=\,?\,\left(\mathrm{J}\right)\)
Z tabulek:
\(\varepsilon_0\,=\,8{,}85{\cdot} 10^{-12}\,\mathrm{ C^2\,N^{-1}\,m^{-2}}\)
\[\begin{eqnarray} W\,&=&\,\frac{Q_3\left(Q_1-Q_2\right)}{4 \pi \epsilon_0} \,\left(\frac{1}{a} - \frac{1}{b} \right)\\ W\,&=&\,\frac{3{\cdot}10^{-6}\left(-5{\cdot}10^{-6}-2{\cdot}10^{-6}\right)}{4 \pi\cdot 8{,}85{\cdot} 10^{-12}} \,\cdot\left(\frac{1}{1{,}5{\cdot}10^{-1}} - \frac{1}{5{\cdot}10^{-2}} \right)\,\mathrm{J}\\ W\,&=&\,2{,}5 \, \mathrm{J}\end{eqnarray}\]Odpověď
Při přenesení náboje z vrcholu A do vrcholu B obdélníka vykoná elektrická síla práci
\[W\,=\,\frac{Q_3\left(Q_1-Q_2\right)}{4 \pi \epsilon_0} \,\left(\frac{1}{a} - \frac{1}{b} \right)\,=\,2{,}5\,\mathrm{J}.\]Co když vyjde práce záporná?
Pokud je práce vykonaná elektrickou silou záporná, znamená to, že se náboj přesunul z místa s menší elektrickou potenciální energií do místa s větší elektrickou potenciální energií. V takovém případě nevykonala práci elektrická síla, ale práci vykonala vnější síla.
Je to stejné jako v tíhovém poli. Pokud těleso padá (pohybuje se z místa s vyšší potenciální energií do místa s nižší potenciální energií) koná práci tíhová síla. Naopak pokud chceme, aby se těleso dostalo z místa s nižší potenciální energií do místa s vyšší potenciální energií, musí vykonat práci vnější síla.
Práce vykonaná elektrickou silou a vnější silou je stejně velká, ale podle používané konvence se liší znaménkem.





