Sbírka řešených úloh

Magnetická indukce v bodech na rovině souměrnosti dvou přímých vodičů

Úloha číslo: 470

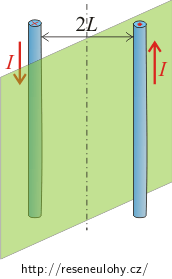
Dva tenké nekonečné rovnoběžné vodiče jsou umístněny ve vzdálenosti 2L. Oběma prochází proud I. Směry proudů ve vodičích jsou opačné. Určete velikost a směr magnetické indukce v bodech roviny souměrnosti (tj. na rovině uprostřed mezi vodiči).

• Nápověda

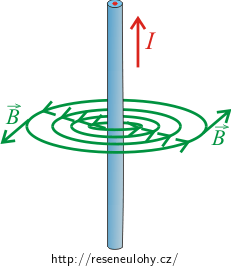
  Nakreslete si magnetické pole, které ve svém okolí vytváří přímý vodič s proudem.

  Výsledný vektor magnetické indukce se rovná součtu vektorů magnetických indukcí od obou vodičů.

• Řešení nápovědy – Magnetické pole přímého vodiče s proudem

  V okolí vodiče, kterým prochází elektrický proud, se vytváří magnetické pole charakterizované magnetickou indukcí. Indukční čáry vektoru magnetické indukce \(\vec{B}\) mají tvar soustředných kružnic se středem ve vodiči.

  

  Směr vektoru magnetické indukce \(\vec{B}\) určíme pomocí Ampérova pravidla pravé ruky a to tak, že položíme palec pravé ruky ve směru proudu ve vodiči a zahnuté prsty ukazují směr magnetických indukčních čar.

  Pro velikost vektoru magnetické indukce B od dlouhého přímého vodiče s proudem platí vztah

  \[B= \frac{\mu_\mathrm0}{2\pi}\,\frac{I}{R},\]

  kde I je proud procházející vodičem a R je kolmá vzdálenost od vodiče, ve které určujeme velikost magnetické indukce.

  Podrobné odvození tohoto vztahu naleznete v úloze Magnetické pole dlouhého přímého vodiče s proudem.

• Rozbor

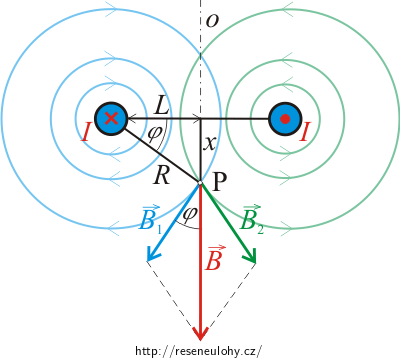
  Velikost výsledné magnetické indukce určíme v obecném bodě P na rovině souměrnosti o, která je kolmá k rovině vodičů. Velikost výsledné magnetické indukce v tomto bodě se rovná vektorovému součtu vektorů magnetických indukcí od obou vodičů. Protože vodiči prochází proudy o stejné velikosti a bod, v němž určujeme výslednou magnetickou indukci, je od obou vodičů stejně vzdálen, budou mít magnetické indukce od obou vodičů v tomto bodě stejnou velikost. Lišit se budou pouze směrem, který určíme pomocí Ampérova pravidla pravé ruky.

• Řešení

  Vektor výsledné magnetické indukce v bodě P na rovině souměrnosti o mezi vodiči určíme jako součet vektorů magnetických indukcí od jednotlivých vodičů:

  \[\vec{B}=\vec{B_1}+\vec{B_2}.\]

  Směry jednotlivých magnetických indukcí určíme pomocí Ampérova pravidla pravé ruky (viz obrázek).

  

  Protože vodiči prochází stejně veliké proudy, vytváří v bodě P na rovině souměrnosti o magnetická pole o stejných velikostech. Pro jejich velikosti platí vztah

  \[B_1=B_2=\frac{\mu_\mathrm{0}}{2\pi}\,\frac{I}{R},\]

  kde I je proud procházející každým z vodičů a R je vzdálenost bodu P od vodiče, kterou vyjádříme jako

  \[R=\sqrt{L^2+x^2}.\]

  Pro velikost magnetické indukce B₁ tak platí

  \[B_1=\frac{\mu_\mathrm{0}}{2\pi}\,\frac{I}{\sqrt{L^2+x^2}}.\]

   

  Z obrázku vyplývá, že výsledná magnetická indukce \(\vec{B}\) bude ležet v rovině souměrnosti o. Její velikost B získáme tedy sečtením velikostí průmětů obou vektorů \(\vec{B_1}\) a \(\vec{B_2}\) do roviny o, tzn.

  \[B=B_1\cos{\varphi}+B_2\cos{\varphi}=2B_1\cos{\varphi}.\tag{1}\]

  Úhel φ vyjádříme pomocí vlastností pravoúhlého trojúhelníku (viz obrázek) jako

  \[\cos{\varphi}=\frac{L}{R}=\frac{L}{\sqrt{L^2+x^2}}.\]

  Vztahy pro velikost vektoru B₁ a cosφ dosadíme do rovnice (1) pro velikost celkové magnetické indukce B:

  \[B=2\frac{\mu_\mathrm{0}}{2\pi}\,\frac{I}{\sqrt{L^2+x^2}}\,\frac{L}{\sqrt{L^2+x^2}}.\] Výraz upravíme a získáme vztah pro velikost magnetické indukce B v libovolném bodě P na rovině souměrnosti o mezi vodiči: \[B=\frac{\mu_\mathrm{0}IL}{\pi(L^2+x^2)}.\]

• Odpověď

  Vektor celkové magnetické indukce v bodech roviny souměrnosti leží v této rovině. Pro jeho velikost jsme odvodili vztah

  \[B=\frac{\mu_\mathrm{0}IL}{\pi(L^2+x^2)}.\]

• Komentář – Magnetická indukce ve středu mezi vodiči

  Vztah pro velikost výsledné magnetické indukce v rovině souměrnosti obou vodičů ověříme tím, že určíme velikost magnetické indukce ve středu mezi vodiči. To znamená, že do vztahu

  \[B=\frac{\mu_\mathrm{0}IL}{\pi(L^2+x^2)},\]

  dosadíme x = 0.

  Pro magnetickou indukci ve středu mezi vodiči pak platí vztah

  \[B=\frac{\mu_\mathrm{0}I}{\pi L},\]

  který odpovídá součtu magnetických indukcí od jednotlivých vodičů s proudy o stejné velikosti a směru.