Krátký a dlouhý solenoid
Úloha číslo: 256
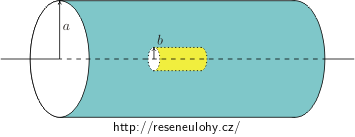
Krátký solenoid délky l, s poloměrem b a n2 závity na jednotku délky leží v ose velmi dlouhého solenoidu o poloměru a (přitom a > b) a n1 závity na jednotku délky.
Krátkým solenoidem protéká proud I. Jaký je magnetický indukční tok dlouhým solenoidem? Určete konstantu vzájemné indukčnosti tohoto uspořádání solenoidů.
Než se pustíte do řešení, můžete se také podívat na obdobnou jednodušší úlohu Vzájemná indukčnost cívek.
Nápověda 1
Jaký je vztah mezi indukčním tokem v dlouhém solenoidu, proudem v krátkém solenoidu a konstantou vzájemné indukčnosti?
Jaký je vztah mezi indukčním tokem v krátkém solenoidu, proudem v dlouhém solenoidu a konstantou vzájemné indukčnosti?
Liší se konstanta vzájemné indukčnosti v obou případech?
Nápověda 2
V úloze máme najít indukční tok dlouhým solenoidem vyvolaný proudem v solenoidu krátkém. Počítání přímo podle definice indukčního toku je obtížně proveditelné, pole krátkého solenoidu má (zvláště vně něj) složitý průběh. Pomohlo by nám, pokud bychom znali konstantu vzájemné indukčnosti.
Uměli byste vyřešit opačnou (duální) úlohu — stanovit indukční tok krátkým solenoidem při proudu tekoucím dlouhým solenoidem? V dlouhém solenoidu přece magnetické pole můžeme považovat za homogenní.
Jak nám řešení této duální úlohy pomůže?
Rozbor
Úlohu není možné řešit pouze tak, že pole je uvnitř krátkého solenoidu homogenní a vně něj není žádné, protože indukční čáry jsou pochopitelně uzavřené a uzavírají se právě v okolí malého solenoidu. Není také dost dobře možné počítat přímou integrací, protože pole vně krátkého solenoidu a na jeho okrajích je velmi složité.
Vyjdeme tedy z definice vzájemné indukčnosti M, podle které platí:
\[\Phi_1 = M_{12}I_2, \qquad \Phi_2 = M_{21}I_1, \qquad M_{21} = M_{12} = M.\]Stačí tedy zkoumat duální problém: jaký je tok krátkým solenoidem, jestliže dlouhým protéká proud. Oba toky jsou shodné.
Pole uvnitř dlouhého solenoidu je (dobře) homogenní a okrajové části a vnější část pole leží mimo krátký solenoid. Proto můžeme použít jednoduchého vztahu pro magnetickou indukci pole v dlouhém solenoidu a indukční tok krátkým solenoidem pak spočteme jako součin magnetické indukce, hustoty závitů, délky krátkého solenoidu a plochy jednoho jeho závitu.
Řešení
Budeme řešit duální problém: Jaký je tok Φ2 krátkým solenoidem, jestliže dlouhým protéká proud I1. Náš původní problém má podle vztahů uvedených v rozboru úlohy stejné řešení.
Pole v dlouhém solenoidu je na počítání mnohem jednodušší, neboť je (s velkou přesností) homogenní. Jestliže dlouhým solenoidem protéká proud I1, magnetický indukční tok krátkým solenoidem je
\[\Phi_2 = N_2S_2B_1 = n_2l\pi b^2B_1,\]kde N2 = n2l je počet závitů krátkého solenoidu, S2 = πb2 plocha závitu krátkého solenoidu a za B1 dosadíme ze vztahu pro magnetickou indukci uvnitř dlouhého solenoidu B1 = μ0n1I1:
\[\Phi_2 = \mu_0n_1n_2l\pi b^2I_1.\]Jestliže je proud krátkým solenoidem I2 = I1 = I, potom magnetický indukční tok Φ1 dlouhým solenoidem má podle vztahů výše stejnou velikost jako Φ2.
Pro konstantu M vzájemné indukčnosti platí, že
\[\Phi_2 = MI_1,\]a proto
\[M = \mu_0n_1n_2l\pi b^2.\]Výsledek
Magnetický indukční tok Φ dlouhým solenoidem, jestliže krátkým solenoidem protéká proud I, je určen vztahem
\[\Phi = \mu_0n_1n_2l\pi b^2I.\]Pro konstantu M vzájemné indukčnosti platí, že
\[\Phi = MI,\]a proto
\[M = \mu_0n_1n_2l\pi b^2.\]Komentář ke konstantě vzájemné indukčnosti
Stručně popíšeme, proč jsou konstanty vzájemné indukčnosti M12 a M21 stejné. Odvození provedeme pro jednoduchost na případu dvou smyček s proudy I1 a I2.
Označme Φ1 indukční tok tekoucí první smyčkou s proudem I1 a Φ2 indukční tok tekoucí druhou smyčkou s proudem I2.
Podle Biotova-Savartova-Laplaceova zákona je příspěvek k magnetické indukci \(\vec{B}_1\) od první smyčky (v kterémkoli místě druhé smyčky) přímo úměrný proudu I1 tekoucímu první smyčkou.
V následujícím textu budeme značit S1,2 plochu první, resp. druhé smyčky a ∂S1,2 jejich hranice.
Vyjdeme z definice indukčního toku a vektorového potenciálu a použijeme Stokesovu větu, čímž dostaneme, že příspěvek první smyčky k indukčnímu toku druhou smyčkou je
\[\Phi_2 = \int_\mathrm{S_2} \vec B_1\cdot \mathrm{d}\vec S_2 = \int_\mathrm{S_2} (\nabla\times \vec A_1)\cdot \mathrm{d}\vec S_2 = \oint_\mathrm{\partial S_2} \vec A_1\cdot \mathrm{d}\vec l_2.\]Přitom pro vektorový potenciál \(\vec{A}_1\) pole první smyčky platí obecný vztah
\[\vec A_1 = \frac{\mu_0I_1}{4\pi}\oint_\mathrm{\partial S_1} \frac{ \mathrm{d}\vec l_1}{r},\]kde integrujeme podél hranice první smyčky a r značí vzdálenost elementu \( \mathrm{d}\vec{l}_1\) od místa, kde vektorový potenciál počítáme. Dosazením do vztahu pro indukční tok dostaneme
\[\Phi_2 = \frac{\mu_0I_1}{4\pi}\oint_\mathrm{\partial S_2} \left(\oint_\mathrm{\partial S_1} \frac{ \mathrm{d}\vec l_1}{r}\right)\cdot \mathrm{d}\vec l_2 = \frac{\mu_0I_1}{4\pi}\iint_\mathrm{\partial S_2\times \partial S_1} \frac{ \mathrm{d}\vec l_1\cdot \mathrm{d}\vec l_2}{r},\]odkud porovnáním se vztahem Φ2 = M21I1 dostáváme konstantu vzájemné indukčnosti M21
\[M_{21} = \frac{\mu_0}{4\pi}\iint_\mathrm{\partial S_2\times \partial S_1} \frac{ \mathrm{d}\vec l_1\cdot \mathrm{d}\vec l_2}{r}.\]Tomuto vztahu se někdy říká Neumannův vztah nebo Neumannova formule.
Z tohoto vztahu vyplývá, co jsme naznačili již dříve v úloze: totiž, že konstanta vzájemné indukčnosti závisí pouze na geometrii situace, jmenovitě na relativní vzdálenosti obou smyček a jejich tvaru a velikosti.
Stejným způsobem, pouze záměnou indexů 1 a 2, můžeme odvodit vztah pro konstantu M12 a dostaneme tak hledanou rovnost:
\[M_{12} = \frac{\mu_0}{4\pi}\iint_\mathrm{\partial S_2\times \partial S_1} \frac{ \mathrm{d}\vec l_2\cdot \mathrm{d}\vec l_1}{r} = \frac{\mu_0}{4\pi}\iint_\mathrm{\partial S_1\times \partial S_2} \frac{\ \mathrm{d}\vec l_1\cdot \mathrm{d}\vec l_2}{r} = M_{21}.\]Podobná úloha

