Rezonance v sériovém RLC obvodu
Úloha číslo: 515
Rezistor o elektrickém odporu 50 Ω je zapojen do série s cívkou o indukčnosti 100 mH (odpor vinutí je zanedbatelný) a kondenzátorem o kapacitě 1,0 μF. Obvod je připojen ke zdroji proměnné frekvence při amplitudě napětí 12 V. Určete:
a) amplitudu proudu v obvodu při frekvenci zdroje 50 Hz,
b) určete fázové posunutí mezi napětím a proudem při frekvenci zdroje 50 Hz,
c) frekvenci zdroje, při které je obvod v rezonanci,
d) amplitudu proudu ve stavu rezonance,
e) určete fázové posunutí mezi napětím a proudem při rezonanční frekvenci.
Nápověda – rezonance
Rezonance je stav, kdy obvodem teče největší proud. To nastane, když bude celková impedance obvodu nejmenší (z Ohmova zákona). Toho docílíme tím, že budeme hledat vhodnou frekvenci, při které se kapacitance vyrovná s induktancí a RLC obvod se pak bude chovat pouze jako elektrický odpor (parametry obvodu neměníme, pouze frekvenci napětí zdroje).
Celkovou impedanci sériového RLC obvodu lze obecně získat ze vztahu
\[ Z = \sqrt{ R^2 + (X_\mathrm{L} - X_\mathrm{C})^2} .\]Je patrné, že bude nejmenší, pokud nastane rovnost induktance a kapacitance.
Odvoďte, pro jakou frekvenci nastane rovnost induktance a kapacitance.
Rozbor
Rezonanční frekvenci získáme pomocí Thompsonova vztahu, který je odvozen z rovnosti kapacitance a induktance.
Proud získáme z Ohmova zákona, do kterého dosadíme skutečnost, že při rezonanční frekvenci je kapacitance stejně velká jako induktance.
Fázové posuny získáme pomocí fázorových diagramů. Pro jednotlivé případy (dle frekvencí) je rozlišíme pouze rozdílnými velikostmi fázorů, které se projeví ve velikosti fázového posunu.
Řešení
a) Amplitudu proudu I protékající obvodem při frekvenci f = 50 Hz získáme z Ohmova zákona pro obvod se střídavým napětím:
\[ I = \frac{U}{Z}, \]kde U je amplituda napětí zdroje a Z je celková impedance obvodu, kterou získáme například z fázorového diagramu překresléného pro impedanci. Nápovědu naleznete například v úloze Sériový RLC obvod:
\[ I = \frac{U}{Z}=\frac{U}{\sqrt{R^2 + (X_\mathrm{L}- X_\mathrm{C})^2}} = \frac{U}{\sqrt{R^2 + (\omega L - \frac{1}{\omega C})^2}}=\frac{U}{\sqrt{R^2 + (2 \pi f L - \frac{1}{2 \pi f C})^2}}.\]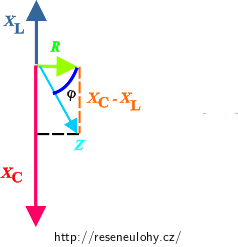
b) Fázový posun φ získáme pomocí stejného fázorového diagramu uvedeného v oddíle výše:
\[ \mathrm{tg} \varphi = \frac{X_\mathrm{L}-X_\mathrm{C}}{R}=\frac{\omega L - \frac{1}{\omega C}}{R}=\frac{2 \pi f L - \frac{1}{2 \pi f C}}{R}.\]
c) Rezonanční frekvenci fr vypočteme pomocí vztahu (jeho odvození je uvedeno v nápovědě):
\[f_\mathrm{r}=\frac{1}{2 \pi\,\sqrt{LC}}.\]
d) Amplitudu proudu v obvodu Ir při rezonanční frekvenci fr vypočteme z Ohmova zákona pro obvod se střídavým napětím, kde se celková impedance obvodu rovná elektrickému odporu:
\[ I_\mathrm{r} = \frac{U}{R}. \]
e) Fázový posun φr získáme pomocí fázorového diagramu pro rezonanční obvod, kde se kapacitance rovná induktanci:
\[ {\varphi}_\mathrm{r} = 0 ^{\circ}.\]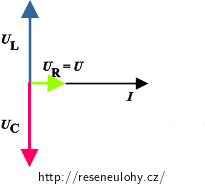
Zápis a číselné dosazení
R = 50 Ω elektrický odpor rezistoru L = 100 mH = 0,1 H indukčnost cívky C = 1,0 μF = 1,0·10-6 F kapacita kondenzátoru U = 12 V amplituda napětí zdroje f = 50 Hz frekvence zdroje I = ? (A) amplituda proudu při frekvenci 50 Hz φ = ? (°) fázový posun mezi napětím a proudem při frekvenci 50 Hz fr = ? (Hz) rezonanční frekvence Ir = ? (A) amplituda proudu při rezonanční frekvenci φr = ? (°) fázový posun mezi napětím a proudem při rezonanční frekvenci
a)
\[I=\frac{U}{\sqrt{R^2 + (2 \pi f L - \frac{1}{2 \pi f C})^2}}=\frac{12}{\sqrt{50^2 + (2\cdot \pi\cdot50{\cdot} 0{,}1 - \frac{1}{2\cdot \pi \cdot 50 {\cdot} 10^{-6}})^2}}\,\dot=\,3{,}8\,\mathrm{mA}\]b)
\[ \mathrm{tg}\, \varphi =\frac{2 \pi f L - \frac{1}{2 \pi f C}}{R}=\frac{2 \cdot \pi \cdot 50 {\cdot} 0{,}1 - \frac{1}{2\cdot \pi\cdot 50 {\cdot} 10^{-6}}}{50}\,\dot=\,-63 \ \Rightarrow \ \varphi \,\dot=\, -89^{\circ}\]c)
\[f_\mathrm{r}=\frac{1}{2\pi\,\sqrt{LC}}=\frac{1}{2\pi\,\sqrt{0{,}1 {\cdot} 10^{-6}}}\,\dot=\, 500\,\mathrm {Hz}\]d)
\[I_r = \frac{U}{R}= \frac{12}{50}=0{,}24\,\mathrm A\]e) viz Řešení:
\[{\varphi}_\mathrm{r} = 0 ^{\circ}.\]Odpověď
Proud v obvodu při frekvenci 50 Hz je asi 3,8 mA a fázový posun mezi napětím a proudem se přibližně rovná −89°, což znamená, že proud předbíhá napětí.
Rezonanční frekvence obvodu je přibližně 500 Hz, proud tekoucí obvodem při této frekvenci je 0,24 A.
Fázový posun mezi napětím a proudem při rezonanční frekvenci je nulový, tzn. napětí je ve fázi s proudem.


