Proudová smyčka ve tvaru U
Úloha číslo: 2283
Nekonečně dlouhý vodič protékaný proudem I je ohnut do tvaru U tak, jak je znázorněno na obrázku. Určete magnetické pole v bodě P, který leží ve středu polokružnice.
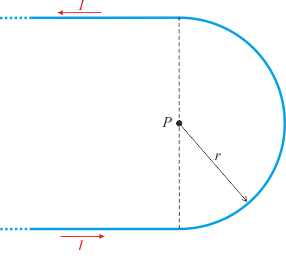
Nápověda
V řešení úlohy využijeme výsledků z úloh Magnetické pole dlouhého přímého vodiče s proudem a Magnetická indukce na ose kruhového závitu. Pokud jste úlohy neřešili, doporučuji je první vyřešit a pak se vrátit k této úloze.
Z úlohy Magnetické pole dlouhého přímého vodiče s proudem, Odpověď využijeme vztah pro velikost magnetické indukce, kterou v bodě P vytváří přímý vodič konečné délky, jímž protéká proud I:
\[B=\frac{\mu_0}{4\pi}\frac{I}{R}(\cos\alpha-\cos\beta).\]Význam úhlů \(\alpha\) a \(\beta\) ilustruje následující obrázek a \(R\) označuje vzdálenost bodu P a přímky, na které vodič leží.
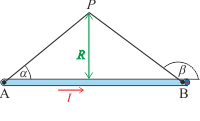
Z úlohy Magnetická indukce na ose kruhového závitu, Magnetické pole ve středu půlkruhového závitu využijeme vztah pro velikost magnetické indukce ve středu půlkruhového závitu o poloměru r, kterým protéká proud I:
\[B=\frac{\mu_0}{4}\frac{I}{r}.\]Uvědomte si, že magnetická indukce je vektorová veličina. Proto nemůžeme spočítat velikosti příspěvků od jednotlivých částí proudové smyčky a pak je sečíst. Musíme provést vektorový součet, tedy uvažovat směry jednotlivých příspěvků.
Jakým způsobem rozdělíme zadaný vodič?
Nápověda – směry magnetické indukce od jednotlivých částí
Pro určení směru magnetické indukce od jednotlivých částí připomeňme vzorec pro elementární příspěvek k magnetické indukci, tzv. Biotův-Savartův zákon (Magnetické pole dlouhého přímého vodiče s proudem, Řešení nápovědy):
\[\mathrm{d}\vec{B}=\frac{\mu_0}{4\pi}\frac{I\mathrm{d}\vec{x}\times\vec{r}}{r^3},\]kde \(\vec{x}\) je vektor ve směru protékajícího proudu v místě elementárního kousku drátu a \(\vec{r}\) je vektor spojující infinitezimální kousek drátu a bod, v němž magnetickou indukci počítáme. Výsledný směr \(\mathrm{d}\vec{B}\) určíme pomocí pravidla pravé ruky pro vektorový součin, kde ukazováček míří ve směru \(\mathrm{d}\vec{x}\), prostředníček je ve směru \(\vec{r}\) a palec ukazuje výsledný směr příspěvku magnetické indukce \(\mathrm{d}\vec{B}\).
Řešení

Vodič rozdělíme na tři části a výslednou magnetickou indukci získáme jako vektorový součet jednotlivých příspěvků:
\[\vec{B_\mathrm{P}}=\vec{B_1}+\vec{B_2}+\vec{B_3},\tag{0}\]kde \(\vec{B_1}\) je příspěvek od spodní vodorovné části, \(\vec{B_2}\) je příspěvek od horní vodorovné části a \(\vec{B_3}\) je příspěvek od půlkruhové části.
Pro výpočet \(\vec{B_1}\) a \(\vec{B_2}\) využijme vztah pro magnetické pole přímého vodiče, který jsme připomněli v nápovědě. Začněme výpočtem magnetické indukce od spodní vodorovné části.
Pro velikost magnetické indukce přímého vodiče konečné délky v libovolném bodě P platí
\[ B=\frac{\mu_0}{4\pi}\frac{I}{R}(\cos\alpha-\cos\beta),\tag{1}\]kde R je vzdálenost bodu P od přímého vodiče, v našem případě
\[R=r.\]Nyní potřebujeme vyjádřit hodnoty \(\cos\alpha\) a \(\cos\beta\) (význam úhlů viz nápověda). Jelikož vodič pokračuje ve vodorovném směru do nekonečna, je zřejmé, že úhel \(\alpha=0°\) a
\[\cos\alpha=1.\]Z obrázku je patrné \(\beta=90°\) a
\[\cos\beta=0.\]Dosadíme-li poslední tři poznatky do rovnice (1), získáme
\[B_1=\frac{\mu_0}{4\pi}\frac{I}{r}.\tag{A}\]Snadno zjistíme, že velikost příspěvku magnetické indukce od horní vodorovné části je stejná jako velikost příspěvku od spodní vodorovné části:
\[B_2=\frac{\mu_0}{4\pi}\frac{I}{r}.\tag{B}\]Hodnotu příspěvku od půlkruhové části určíme využitím poznatků z nápovědy. Velikost magnetické indukce ve středu půlkruhového závitu o poloměru r, kterým protéká proud I, je
\[B_3=\frac{\mu_0}{4}\frac{I}{r}.\tag{C}\]Nyní se vraťme k rovnici (0) a dosaďme do ní spočítané hodnoty ((A), (B) a (C)). Je důležité připomenout, že se jedná o součet vektorů, proto musíme při součtu uvažovat směry jednotlivých příspěvků. V našem případě je to jednoduché, jelikož všechny vektory mají stejný směr (viz nápověda):
\[\vec{B_\mathrm{P}}=\vec{B_1}+\vec{B_2}+\vec{B_3},\] \[B_\mathrm{P}=\frac{\mu_0}{4\pi}\frac{I}{r} + \frac{\mu_0}{4\pi}\frac{I}{r}+\frac{\mu_0}{4}\frac{I}{r},\] \[B_\mathrm{P}=\frac{\mu_0 I}{4\pi r}(2+\pi).\]Směr výsledného vektoru magnetické indukce je ven z nákresny.
Odpověď
Magnetické pole v bodě P má velikost \({B_\mathrm{P}}=\frac{\mu_0 I}{4\pi r}(2+\pi)\) a směr ven z nákresny.
Komentář − další případy kružnicového oblouku
Kružnicový oblouk příslušný úhlu \(\frac{\pi}{2}\)
Zamysleme se nad situací, kdy by prostřední část vodiče byla tvořena namísto půlkružnicí kružnicovým obloukem příslušným úhlu \(\frac{\pi}{2}\), jak ukazuje následující obrázek.
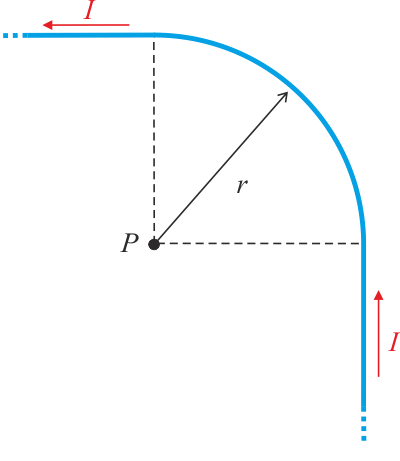
Tento případ budeme řešit analogicky jako situaci s půlkružnicí, tedy rozdělíme vodič na tři části a výslednou magnetickou indukci získáme jako vektorový součet jednotlivých příspěvků:
\[\vec{B_\mathrm{P}}=\vec{B_1}+\vec{B_2}+\vec{B_3},\]kde \(\vec{B_1}\) je příspěvek od spodního přímého vodiče, \(\vec{B_2}\) je příspěvek od horního přímého vodiče a \(\vec{B_3}\) je příspěvek od kružnicového oblouku.
Uvědomme si, že příspěvek k magnetické indukci od první a druhé části vodiče je stejný jako v případě půlkružnicového oblouku, jelikož vzdálenost se nemění a také úhly \(\alpha\) a \(\beta\) zůstávají stejné:
\[B_1=B_2=\frac{\mu_0}{4\pi}\frac{I}{r}.\]Velikost příspěvku od kružnicového oblouku spočítáme pomocí vztahu uvedeného v úloze Magnetická indukce na ose kruhového závitu, Magnetické pole ve středu půlkruhového závitu. Jedná se o vztah pro magnetické pole ve středu kružnicového oblouku o velikosti \(\beta\):
\[B=\frac{\mu_0 \beta}{4\pi}\frac{I}{r}.\tag{*}\]Po dosazení \(\beta=\frac{\pi}{2} \) dostaneme:
\[B_3=\frac{\mu_0 }{8}\frac{I}{r}.\]Nyní se zamysleme nad směry jednotlivých příspěvků. Ze stejných důvodů jako v případě půlkružnicového oblouku musí být každý z příspěvků kolmý na nákresnu. Orientaci jednotlivých příspěvků pak opět určíme pomocí Ampérova pravidla pravé ruky. Tudíž výsledné magnetické pole bude
\[B_\mathrm{P}=\frac{\mu_0}{4\pi}\frac{I}{r}+\frac{\mu_0}{4\pi}\frac{I}{r}+\frac{\mu_0 }{8}\frac{I}{r},\] \[B_\mathrm{P}=\frac{\mu_0}{8\pi r} (4+\pi).\]Kružnicový oblouk o úhlu \(\frac{3\pi}{2}\)
Nyní uvažujme stejnou situaci jako v předchozím případě, s tím rozdílem, že úhel příslušný ke kružnicovému oblouku se změní na \(\frac{3\pi}{2}\).
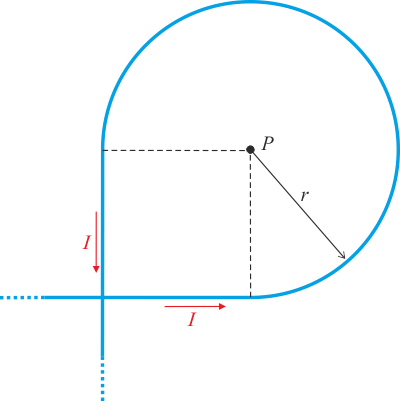
Výpočet bude probíhat úplně stejným způsobem, tudíž některé kroky přeskočíme. Velikost příspěvků od přímých vodičů se nezmění:
\[B_1=B_2=\frac{\mu_0}{4\pi}\frac{I}{r}.\]Velikost příspěvku od kružnicového oblouku opět vypočítáme pomocí vztahu (*) za \(\beta\) dosadíme \(\frac{3\pi}{2} \)
\[B_3=\frac{3\mu_0 }{8}\frac{I}{r}.\]Směry musí opět být kolmé na nákresnu a orientaci určíme opět pomocí Ampérova pravidla pravé ruky, tudíž výsledné magnetické pole bude
\[B_P=\frac{\mu_0}{4\pi}\frac{I}{r}+\frac{\mu_0}{4\pi}\frac{I}{r}+3\frac{\mu_0 }{8}\frac{I}{r},\] \[B_P=\frac{\mu_0}{8\pi r} (4+3\pi).\]Kružnicový oblouk o úhlu \(\beta\)
Zobecnění na obecný kružnicový oblouk příslušný úhlu \(\beta\) už nebude obtížné, jelikož výpočet bude probíhat stejně jako v předchozích dvou případech. Tudíž
\[B_1=B_2=\frac{\mu_0}{4\pi}\frac{I}{r},\] \[B_3=\frac{\mu_0 \beta}{4\pi}\frac{I}{r}.\]Směry musí být znovu kolmé na nákresnu a orientaci určíme pomocí Ampérova pravidla pravé ruky, tudíž výsledné magnetické pole bude
\[B_\mathrm{P}=\frac{\mu_0}{4\pi}\frac{I}{r}+\frac{\mu_0}{4\pi}\frac{I}{r}+\frac{\mu_0 \beta}{4\pi}\frac{I}{r},\] \[B_\mathrm{P}=\frac{\mu_0}{4\pi r} (2+\beta).\]

