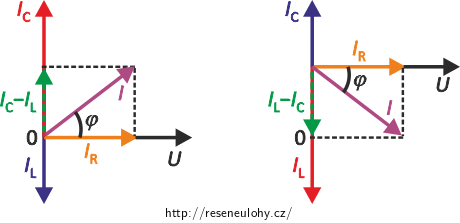
Paralelní RLC obvod
Úloha číslo: 623
Rezistor, ideální kondenzátor a ideální cívka jsou paralelně připojeny ke zdroji střídavého napětí 160 V a frekvence 250 Hz. Rezistorem prochází proud 2 A, ideální cívkou 0,8 A a celkový proud je 2,5 A. Určete odpor rezistoru, kapacitu ideálního kondenzátoru a indukčnost ideální cívky (předpokládejte IC > IL).
Pozn.: Mluvíme-li o proudu či napětí, myslíme efektivní hodnoty proudu či napětí.
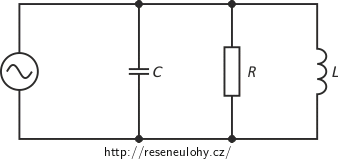
Nápověda – schéma zapojení
Nápověda – fázorový diagram
Fázorový diagram pro paralelní zapojení prvků v obvodu se střídavým proudem kreslíme analogicky jako v obvodu sériovém. Musíme zohlednit to, že v sériovém zapojení je na všech prvcích stejný proud, zatímco v obvodu zapojeném paralelně je na všech prvcích stejné napětí.
Postup pro sestavení fázorového diagramu pro paralelní RLC obvod: V pomyslném směru osy x zakreslíme fázor napětí a fázor proudu protékajícího rezistorem, v kladném směru osy y zakreslujeme fázor proudu protékajícího kondenzátorem a v záporném směru osy y zakreslujeme fázor proudu protékajícího cívkou.
Zápis
U = 160 V napětí zdroje f = 250 Hz frekvence napětí zdroje IR = 2 A proud protékající rezistorem IL = 0,8 A proud protékající ideální cívkou I = 2,5 A celkový proud obvodu R = ? (Ω) odpor rezistoru C = ? (F) kapacita kondenzátoru L = ? (H) indukčnost cívky Rozbor
Hledané veličiny získáme pomocí Ohmova zákona pro střídavý proud, který budeme aplikovat vždy na příslušnou součástku. Protože se jedná o paralelní zapojení, je na všech větvích (tj. na všech součástkách) stejné napětí jako na zdroji.
Neznámý proud kondenzátorem určíme ze zadaných proudů pomocí fázorového diagramu pro paralelní zapojení RLC obvodu.
Řešení a číselné dosazení
Odpor rezistoru R:
Protože se jedná o paralelní zapojení, je napětí na rezistoru UR stejné jako napětí zdroje U. Ohmův zákon pro obvod se střídavým proudem lze tedy psát ve tvaru
\[ U = I_\mathrm{R} R, \]kde IR je efektivní hodnota proudu protékajícího rezistorem. Ze vztahu vyjádříme odpor rezistoru R:
\[ R = \frac{U}{I_\mathrm{R}}. \]Dosadíme číselné hodnoty:
\[ R = \frac{160}{2}\,\mathrm \Omega = 80\,\mathrm \Omega. \]
Indukčnost cívky L:
Napětí na cívce UL je také stejné, jako je napětí zdroje U, a lze ho vyjádřit z Ohmova zákona pro obvod se střídavým proudem:
\[ U= X_\mathrm{L} I_\mathrm{L} = 2 \pi f L\, I_\mathrm{L}, \]kde XL je induktance cívky, f napětí zdroje, L indukčnost cívky a IL je efektivní hodnota proudu protékajícího cívkou.
Vyjádříme indukčnost L:
\[ L = \frac{U}{2 \pi f I_\mathrm{L}}. \]Dosadíme číselné hodnoty:
\[ L = \frac{160}{2 \cdot \pi \cdot 250 {\cdot} 0{,}8}\,\mathrm H \,\dot=\, 0{,}13 \,\mathrm H. \]
Kapacita kondenzátoru C:
Kapacitu kondenzátoru C odvodíme také z Ohmova zákona pro obvod se střídavým proudem:
\[ U = X_\mathrm{C} I_\mathrm{C} =\frac{I_\mathrm{C}}{2 \pi f C},\]kde XC je kapacitance kondenzátoru, f frekvence napětí zdroje, C kapacita kondenzátoru a IC je efektivní hodnota proudu protékajícího kondenzátorem. Napětí na kondenzátoru je opět stejné jako napětí zdroje U.
Vyjádříme kapacitu kondenzátoru C:
\[ C =\frac{I_\mathrm{C}}{2 \pi f U}.\]Pro odvození velikosti efektivní hodnoty proudu protékajícího kondenzátorem IC nakreslíme fázorový diagram pro proudy, přičemž víme, že IC > IL:
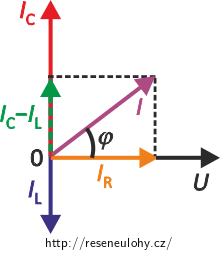
Z fázorového diagramu vyjádříme vztah mezi proudy:
\[ I^2 = (I_\mathrm{C} - I_\mathrm{L})^2 + I_\mathrm{R}^2. \]Upravíme:
\[ I^2 = I_\mathrm{C}^2 - 2I_\mathrm{L} I_\mathrm{C} +I_\mathrm{L}^2 + I_\mathrm{R}^2 \] \[ 0 = I_\mathrm{C}^2 - 2I_\mathrm{L} I_\mathrm{C} +(I_\mathrm{L}^2 + I_\mathrm{R}^2 - I^2).\]Řešíme kvadratickou rovnici pro neznámou IC:
\[(I_\mathrm{C})_{1{,}2} = \frac{ 2 I_\mathrm{L} \pm \sqrt{ (2 I_\mathrm{L})^2 - 4 (I_\mathrm{L}^2 + I_\mathrm{R}^2 -I^2)}}{2}. \]Upravíme:
\[(I_\mathrm{C})_{1{,}2} = I_\mathrm{L} \pm \sqrt{ ( I_\mathrm{L})^2 - (I_\mathrm{L}^2 + I_\mathrm{R}^2 -I^2)} \] \[(I_\mathrm{C})_{1{,}2} = I_\mathrm{L} \pm \sqrt{ I^2 - I_\mathrm{R}^2 }. \]Dosadíme zadané hodnoty:
\[(I_\mathrm{C}C)_{1} = 0{,}8 + \sqrt{ 2{,}5^2 - 2^2 }\,\mathrm A= 2{,}3 \,\mathrm A \] \[(I_\mathrm{C}C)_{2} = 0{,}8 - \sqrt{ 2{,}5^2 - 2^2 }\,\mathrm A= -0{,}7\,\mathrm A .\]Fyzikální význam má pouze efektivní hodnota proudu IC = 2,3 A.
Dosadíme do vztahu pro výpočet kapacity kondenzátoru C z Ohmova zákona, který jsme odvodili výše:
\[ C =\frac{I_\mathrm{C}}{2 \pi f U}= \frac{2{,}3}{2 \cdot \pi \cdot 250 {\cdot} 160}\,\mathrm F \,\dot=\, 9{,}2 {\cdot} 10^{-6} \,\mathrm F = 9{,}2 \,\mathrm{ \mu F}. \]Odpověď
Odpor rezistoru má hodnotu 80 Ω, indukčnost cívky je přibližně 0,13 H a kapacita kondenzátoru asi 9,2 μF.