Válcový kondenzátor
Úloha číslo: 449
Válcový kondenzátor tvoří dva dlouhé soustředné válce o poloměrech a a b, kde a < b. Vypočítejte kapacitu kondenzátoru.
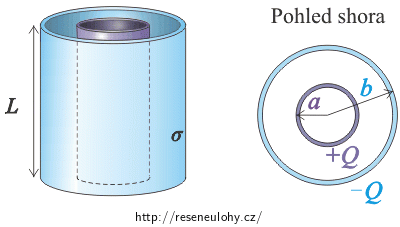
Pozn.: Zanedbejte okrajové efekty na koncích kondenzátoru.
Nápověda: Kapacita
Představme si, že kondenzátor nabijeme nábojem Q. Mezi nábojem, napětím na kondenzátoru a kapacitou kondenzátoru platí vztah:
\[C\,=\,\frac{Q}{U}\,.\]Abychom mohli vyjádřit kapacitu kondenzátoru, musíme tedy určit, jaké je napětí mezi deskami.
Uvědomte si, jak souvisí napětí mezi elektrodami, tj. válci kondenzátoru, s potenciálem a intenzitou elektrického pole mezi nimi.
Nápověda: Intenzita pole mezi válci
Využijte výsledku úlohy Pole nabité válcové plochy, kde je vypočítaná intenzita v okolí válcové plochy.
Rozbor
Válcový kondenzátor tvoří dvě soustředné válcové plochy, které jsou nabity stejně velkým nábojem opačného znaménka.
Kapacita kondenzátoru je přímo úměrná náboji a nepřímo úměrná napětí mezi válci kondenzátoru.
Napětí mezi válci, tedy rozdíl potenciálů na deskách, bude rovno integrálu intenzity podél spojnice obou elektrod. (Podrobnější vysvětlení naleznete v první nápovědě.)
Intenzita vně válcové plochy nepřímo úměrně klesá se vzdáleností od osy válcové plochy a uvnitř plochy je rovna nule (viz úloha Pole nabité válcové plochy). Mezi válci je tedy intenzita nepřímo úměrná vzdálenosti od osy válcových ploch. Vnější válec k intenzitě elektrického pole nepřispívá, protože uvnitř válcové plochy je intenzita nulová.
Řešení
Kapacitu C válcového kondenzátoru určíme jako podíl náboje Q na deskách a napětí U mezi nimi:
\[C\,=\,\frac{Q}{U}.\]Velikost napětí mezi válci je rovna práci, kterou je třeba vykonat při přenesení jednotkového náboje z jednoho válce na druhý:
\[U\,=\,\frac{W}{Q}\,=\, \int_\mathrm{a}^\mathrm{b} \frac{F}{Q} \,\mathrm{d}z.\]Podíl elektrické síly F a náboje Q je roven intenzitě E elektrického pole:
\[U\,=\, \int_\mathrm{a}^\mathrm{b} E \,\mathrm{d}z\,,\]kde z je vzdálenost od osy obou válcových ploch.
Intenzita elektrického pole mezi válci je dána intenzitou elektrického pole vnitřního válce. Vnější válec k intenzitě elektrického pole mezi elektrodami nepřispívá. Intenzitu elektrického pole v okolí nabitého válce jsme vyjádřili v úloze Pole nabitého válce. Poloměr válce je roven a:
\[U\,=\, \int_\mathrm{a}^\mathrm{b} \frac{a \sigma}{\epsilon_0} \,\frac{1}{z}\,\mathrm{d}z.\]Vytkneme konstanty před integrál a integrál vypočítáme:
\[U\,=\, \frac{a \sigma}{\epsilon_0} \int_\mathrm{a}^\mathrm{b} \frac{1}{z}\,\mathrm{d}z \,=\, \frac{a \sigma}{\epsilon_0} \,\left[\ln z\right]_a^b \,=\, \frac{a \sigma}{\epsilon_0} \,\left(\ln b \,-\,\ln a \right),\] \[U\,=\, \frac{a \sigma}{\epsilon_0} \,\ln \frac{b}{a}.\tag{*}\]Protože neznáme nábojovou hustotu σ, ale celkový náboj Q, vyjádříme ji pomocí povrchu válce:
\[Q\,=\, \sigma S\,=\, \sigma 2 \pi a L \hspace{40px} \Rightarrow \hspace{40px}\sigma\,=\,\frac{Q}{2 \pi a L}.\]Nábojovou hustotu σ dosadíme zpět do vzorce (*) a výraz upravíme:
\[U\,=\, \frac{a}{\epsilon_0}\,\frac{Q}{2 \pi a L} \,\ln \frac{b}{a}\,=\,\frac{Q}{2 \pi \epsilon_0 L} \,\ln \frac{b}{a}.\]Protože kapacita kondenzátoru je dána vztahem \(C\,=\,\frac{Q}{U}\), můžeme ji z posledního vzorce vyjádřit:
\[C\,=\,\frac{2 \pi \epsilon_0 L}{\ln \frac{b}{a}}. \]Odpověď
Válcový kondenzátor má kapacitu
\[C\,=\,\frac{2 \pi \epsilon_0 L}{\ln \frac{b}{a}} \,.\]Jaká je intenzita vně kondenzátoru?
Mluvíme-li o kondenzátoru, mělo by být elektrické pole pouze mezi jeho elektrodami. Uvnitř malého válce a vně velkého by měla být intenzita elektrického pole rovna nule. V tomto oddíle se přesvědčíme, že to tak opravdu je.
Z úlohy Pole nabité válcové plochy víme, že uvnitř válcové plochy o poloměru R je intenzita elektrického pole rovna nule a vně válcové plochy je intenzita dána vztahem \(E\,=\,\frac{R \sigma}{\varepsilon_0}\frac{1}{z}.\)
Do obrázku si nakreslíme vektory intenzit elektrického pole pro oba válce.
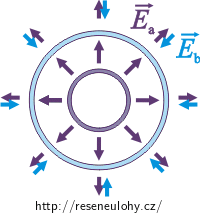
Uvnitř vnitřního válce jsou obě intenzity rovny nule, proto má i výsledné pole nulovou intenzitu.
Mezi válci je nenulová intenzita el. pole malého válce. Celková intenzita je tedy stejná:
\[E\,=\,\frac{a \sigma}{\varepsilon_0}\frac{1}{z}\,,\]kde z nabývá hodnot od a do b.
Tento vztah přepíšeme pomocí celkového náboje Q, kterým je kondenzátor nabit:
\[Q\,=\,\sigma S\,=\,\sigma 2 \pi a L,\] \[E\,=\, \frac{Q}{2 \pi \varepsilon_0 L}\, \frac{1}{z}.\]Vně většího válce mají vektory intenzity stejnou velikost (protože jsou desky nabity stejně velkým nábojem), ale opačný směr (náboje mají opačná znaménka). Výsledná intenzita vně kondenzátoru je tedy rovna nule.
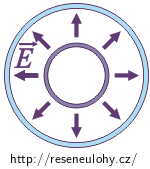
Jak jinak zjistit intenzitu mezi deskami
Intenzitu elektrického pole mezi deskami můžeme získat přímo z Gaussovy věty: \[\int_\mathrm{S} \vec{E} \cdot \mathrm{d}\vec{S}\,=\, \frac{Q}{\varepsilon_0}.\]Jako Gaussovu plochu S volíme povrch válce, jehož osa je stejná s osami obou válcových ploch kondenzátoru. Ze symetrie úlohy je patrné, že je vektor intenzity ve všech místech Gaussovy plochy stejně velký a na plochu kolmý, a proto můžeme integrál na levé straně zjednodušit:
\[\int_\mathrm{S} E \mathrm{d}S\,=\,E \int_\mathrm{S} \mathrm{d}S\,=\, E 2\pi z L.\]Intenzita mezi deskami je tedy dána vztahem:
\[E\,=\, \frac{Q}{2 \pi \varepsilon_0 L}\, \frac{1}{z}\,,\]kde z nabývá hodnot od a do b.
Podrobnější postup řešení naleznete v úloze Pole nabité válcové plochy.
Uvnitř vnitřního válce není v Gaussově ploše uzavřen žádný náboj a intenzita je zde tedy rovna nule.
Vně obou válců je v Gaussově ploše uzavřen náboj +Q a -Q. Dohromady je tedy uvnitř Gaussovy plochy náboj nulový a intenzita je tedy opět rovna nule.



