Sbírka řešených úloh

Vzduchový kondenzátor

Úloha číslo: 1022

• Nápověda 1

  Jak spočítáte kapacitu deskového kondenzátoru?

• Kapacita deskového kondenzátoru

  Kapacita deskového kondenzátoru C se počítá podle vztahu \[C=\frac{\epsilon_0 S}{d},\] kde S je obsah desek kondenzátoru, d vzdálenost desek kondenzátoru a ε₀ je permitivita vakua. Permitivita vzduchu je velmi blízká permitivitě vakua, proto můžeme psát ε₀.

• Nápověda 2

  Po vložení do kondenzátoru se na plechu přemístí náboj, a tak si výsledek můžeme představit jako dva kondenzátory za sebou. Můžeme také uvažovat, že plech vložíme úplně těsně k jedné elektrodě.

• Zápis

  C = 10 pF	kapacita původního kondenzátoru
  d = 1 cm = 1·10-2 m	vzdálenost desek původního kondenzátoru
  x = 1 mm = 1·10-3 m	šířka plechu
  Cv = ? (F)	kapacita nově vzniklého kondenzátoru

• Rozbor

  Uvědomíme si, co znamená vložení plechu do kondenzátoru. Náboj se rozloží na povrchu plechu (viz obrázek) a my dostáváme dva sériově zapojené kondenzátory.

  

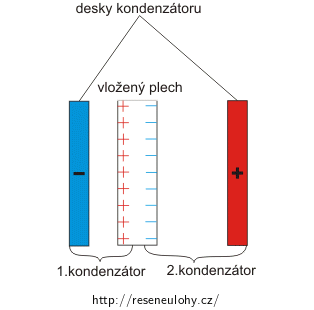
  Výsledná kapacita nezávisí na poloze plechu (podrobněji viz komentář níže), proto si ho představíme těsně u jedné z desek. Dostáváme tak vzduchový kondenzátor, který má vzdálenost mezi deskami zmenšenou o šířku plechu.

• Řešení

  Představíme si, že plech vložíme těsně k jedné desce kondenzátoru. Náboj se rozloží na povrchu plechu. Nově vzniklé zařízení si tedy můžeme představit jako vzduchový kondenzátor, kde vzdálenost desek je rovna původní vzdálenosti d zmenšené o tloušťku plechu x. S využitím vztahu pro kapacitu deskového kondenzátoru můžeme pro kapacitu nového kondenzátoru C_v psát \[ C_\mathrm{v} = \frac{\epsilon_0 S}{d-x}, \] kde ε₀ je permitivita vakua (permitivita vzduchu se téměř rovná permitivitě vakua) a S je obsah desek. Ten se vložením plechu samozřejmě nezmění, a proto jej můžeme vyjádřit ze vztahu pro velikost kapacity původního kondenzátoru C:

  \[ C = \frac{\epsilon_0 S}{d}\qquad \Rightarrow \qquad S=\frac{C d}{\epsilon_0}. \]

  Po dosazení do vztahu pro kapacitu kondenzátoru s plechem C_v získáváme:

  \[ C_\mathrm{v} = \frac{\epsilon_0 S}{d-x}= \frac{\epsilon_0}{d-x}\frac{C d}{\epsilon_0}=C\frac{d}{d-x},\] \[C_\mathrm{v}=10{\cdot}10^{-12} \cdot \frac{1{\cdot}10^{-2}}{1{\cdot}10^{-2}-1{\cdot}10^{-3}} \mathrm F \,\dot{=}\, 11{\cdot}10^{-12}\,\mathrm F \,\dot{=}\, 11\,\mathrm {pF}. \]

• Odpověď

  Kapacita nově vzniklého kondenzátoru je asi 11 pF.

• Komentář – důkaz, že výsledek nezávisí na poloze plechu

  Nyní si výpočtem ověříme, že celková kapacita nového kondenzátoru C_v nezávisí na poloze plechu.

  Nakreslíme si obrázek.

  

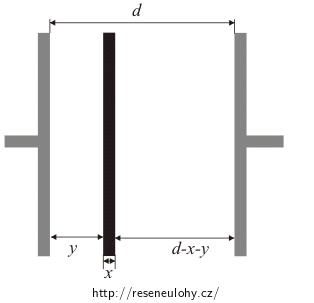
  Z obrázku vidíme, že se jedná o dva sériově zapojené kondenzátory, pro výslednou kapacitu C_v použijeme tedy vztah

  \[\frac{1}{C_\mathrm{v}}=\frac{1}{C_1}+\frac{1}{C_2},\]

  kde C₁ a C₂ jsou kapacity jednotlivých kondenzátorů, jejichž kapacity spočteme podle vztahu uvedeného v nápovědě:

  \[C=\frac{\epsilon_0S}{d}.\]

  Potřebujeme dokázat, že výsledná kapacita C_v nezávisí na poloze plechu. Což znamená, že dokážeme, že nezávisí na vzdálenosti y z obrázku:

  \[\frac{1}{C_\mathrm{v}}=\frac{1}{\frac{\epsilon_0S}{y}}+\frac{1}{\frac{\epsilon_0S}{d-x-y}}=\frac{y}{\epsilon_0S}+\frac{d-x-y}{\epsilon_0S}\] \[C_\mathrm{v}=\frac{\epsilon_0S}{d-x}.\]

  Odtud vidíme, že výsledná kapacita opravdu nezávisí na vzdálenosti y, tj. na poloze plechu.

  Výsledná kapacita nezávisí na poloze vloženého plechu. Můžeme to vidět i z grafu závislosti elektrického potenciálu φ na vzdálenosti l. Mezi deskami kondenzátoru je homogenní pole, proto zde elektrický potenciál roste rovnoměrně se vzdáleností od jedné desky. Zvolme si tedy na levé desce nulový potenciál a nakresleme závislost elektrického potenciálu na vzdálenosti od levé desky. Potenciál ve vodičích je konstantní, proto v prostoru, kde se nachází vložená vodivá deska, potenciál neroste.

  

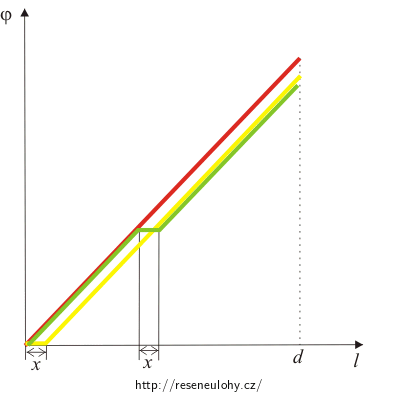
  Červená čára odpovídá situaci, kdy není v kondenzátoru plech, žlutá, když je plech těsně u desky, na které si volíme nulovou hladinu, a zelená, když je plech někde mezi deskami kondenzátoru.