Izolovaná kovová koule
Úloha číslo: 240
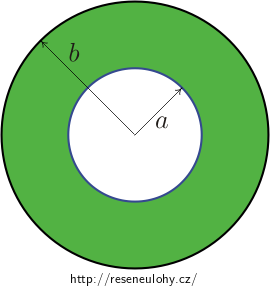
Kovový kulový vodič o poloměru a nese celkový (volný) kladný náboj Q. Koule je obalena vrstvou dielektrika o vnějším poloměru b, které je lineární a jehož permitivita je ε. Vypočtěte potenciál v centru kulového vodiče, jestliže je normován nulou v nekonečnu. Určete také povrchovou a objemovou hustotu vázaného náboje v dielektriku.
Nápověda 1
Uvědomte si sférickou symetrii situace — jaké z ní plyne rozložení volného náboje na povrchu kulového vodiče?
Použijte Gaussovu větu elektrostatiky pro volný náboj a elektrickou indukci
\[\oint_\mathrm{S} \vec D\,\cdot\,d\vec S = Q_\mathrm{volny}.\]V celém prostoru rozlište část uvnitř vodiče a vně vodiče. Není však potřeba rozlišovat část prostoru s dielektrikem a bez něho, protože elektrická indukce závisí pouze na rozložení volného náboje, nikoliv na materiálu prostředí.
Nápověda 2
Využijte toho, že dielektrikum je lineární, a z elektrické indukce vypočtěte intenzitu elektrického pole uvnitř vodiče, vně vodiče v dielektriku a mimo dielektrikum.
Nápověda 3
Potenciál ve středu koule vypočtěte pomocí integrace intenzity elektrického pole ze středu koule do nekonečna. Integrujte po přímé cestě, přitom dbejte na změny prostředí!
Nápověda 4
Ze vztahu pro intenzitu a indukci elektrického pole vypočtěte vektor polarizace v dielektriku. Pomocí něj pak určete hustotu objemového ρb a hustotu povrchového σb vázaného náboje, podle vztahů
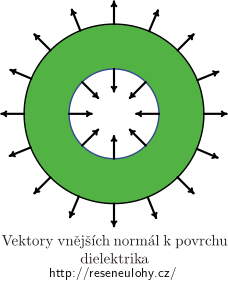
\[\nabla\cdot P = -\varrho_\mathrm{b},\qquad \vec{P}\cdot\vec{n} = \sigma_\mathrm{b},\]kde \(\vec{n}\) značí (vnější) jednotkový normálový vektor mířící ven z plochy. Nezapomeňte, že dielektrikum má povrchy dva!
Rozbor
Situace je sféricky symetrická. Volný náboj se musí rozložit na povrchu kulového vodiče a ze symetrie situace plyne, že se rozloží rovnoměrně.
Tím se vytvoří vně kovové koule pole, které polarizuje lineární dielektrikum okolo ní. Můžeme si představit, že se to projeví vznikem vázaného náboje (na površích a uvnitř dielektrika).
Nyní využijeme Gaussova zákona pro elektrickou indukci. Tato verze zákona uvažuje pouze volný náboj, jehož rozložení a velikost je nám známa na rozdíl od rozložení vázaného náboje. Protože situace je sféricky symetrická, bude elektrická indukce mít radiální směr a tudíž půjde pomocí Gaussova zákona určit její velikost v každém místě prostoru.
Známe-li však elektrickou indukci v každém místě prostoru, pak umíme ihned určit elektrickou intenzitu. V kovovém vodiči a vakuu je to snadné, zde je polarizace nulová. V dielektriku pak využijeme předpokladu, že jde o dielektrikum lineární se známou permitivitou.
Ze znalosti elektrické intenzity pak přímou integrací určíme potenciál.
Nakonec vypočteme vázané náboje v dielektriku. Ze znalosti elektrické indukce a elektrické intenzity v dielektriku určíme vektor polarizace dielektrika a z vektoru polarizace pak vázané náboje.
Řešení — výpočet potenciálu uvnitř koule
Ze sférické symetrie situace můžeme s pomocí Gaussova zákona pro elektrickou indukci
\[\oint \vec D\,\cdot\, d\vec S = Q_{\mathrm{volny}}\]vyvodit, že vektor elektrické indukce vně vodiče míří vždy v radiálním směru a má velikost (zvolenou plochou je kulová plocha s poloměrem r > a a středem ve středu kovové koule):
\[D \,\cdot\, (4\pi r^2) = Q\] \[D = \frac{Q}{4\pi r^2}, \qquad \textrm{ pro } r > a.\]Pokud použijeme v Gaussově zákonu kulovou plochu s poloměrem r < a, není uvnitř ní žádný volný náboj a při uvážení symetrie je tedy elektrická indukce D uvnitř koule nulová:
\[D = 0, \qquad \textrm{pro } r < a.\]V kovovém vodiči tedy zřejmě platí
\[\vec E = \vec P = \vec D = \vec 0.\]Vně vodiče je jednoduché určit intenzitu pole, protože materiál, který obaluje kouli, je dle zadání lineární izotropní dielektrikum. Intenzita má tedy stejný směr jako indukce a má velikost v prostoru dielektrika
\[E = \frac{D}{\varepsilon} = \frac{Q}{4\pi \varepsilon r^2}, \qquad a \,< \,r\, <\, b\]a mimo dielektrikum
\[E = \frac{D}{\varepsilon_0} = \frac{Q}{4\pi \varepsilon_0 r^2}, \qquad r\,>\, b.\]Potenciál ve středu koule spočteme podle vztahu
\[\varphi(0) = \int_0^{\infty} \vec E\cdot d\vec r =\]s přihlédnutím k tomu, že vektory \(\vec{E}\) a \(\rm{d}\vec{r}\) mají stejný směr (od středu koule), neboť náboj Q je kladný:
\[= \int_0^\mathrm{a} 0\,dr + \int_\mathrm{a}^\mathrm{b} \frac{Q}{4\pi\varepsilon}\frac{1}{r^2}\,dr + \int_\mathrm{b}^\infty \frac{Q}{4\pi\varepsilon_0}\frac{1}{r^2}\,dr = \frac{Q}{4\pi}\left(\frac{1}{\varepsilon_0b}+\frac{1}{\varepsilon a}-\frac{1}{\varepsilon b}\right).\]Řešení — výpočet vázaného náboje
Pro vektor polarizace uvnitř lineárního dielektrika platí
\[\vec P = \vec{D} - \varepsilon_0\vec{E} = (\varepsilon-\varepsilon_0)\,\vec{E}\]a podle předchozí části řešení dostaneme po dosazení za \(\vec{E}\)
\[\vec{P} = \frac{(\varepsilon-\varepsilon_0)\,Q}{4\pi\varepsilon r^3}\vec{r}.\]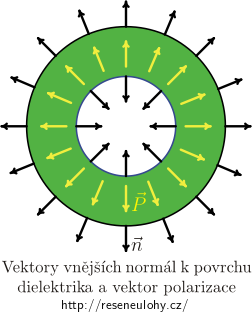
Objemový vázaný náboj je nulový. To ukážeme výpočtem podle vztahu
\[-\varrho_\mathrm{b} = \nabla\,\cdot\, \vec{E} = 0.\]Tuto divergenci intenzity budeme počítat ve sférických souřadnicích. Složky vektoru intenzity v něm mají vyjádření (jde o oblast uvnitř dielektrika):
\[E_\mathrm{r} = \frac{Q}{4\pi\varepsilon}\frac{1}{r^2}, \ E_\theta = E_\phi = 0\]a platí (viz také Diferenciální operátory ve sférických souřadnicích)
\[-\varrho_\mathrm{b} = \nabla\,\cdot\,\vec{E} = \frac{1}{r^2}\frac{\partial}{\partial r}(r^2E_r) + \frac{1}{r\sin\theta}\frac{\partial}{\partial\theta}(E_\theta\sin\theta) + \frac{1}{r\sin\theta}\frac{\partial E_\phi}{\partial\phi} = \frac{1}{r^2}\frac{\partial}{\partial r}\left(\frac{Q}{4\pi\varepsilon}\right) + 0 + 0 = 0 + 0 + 0 = 0,\]neboť derivace konstantní funkce je nulová.
Pro hustotu povrchového náboje dostaneme na vnitřním povrchu (vektor \(\vec{n}\) značí vektor jednotkové vnější normály):
\[\sigma_\mathrm{b,vnitr} = \vec{P}\cdot \vec{n} = -P = -\frac{(\varepsilon-\varepsilon_0)Q}{4\pi\varepsilon a^2},\]protože vektor vnější normály k vnitřnímu povrchu a vektor polarizace mají opačnou orientaci. Na vnějším povrchu mají orientaci stejnou a dostáváme tak
\[\sigma_\mathrm{b,vnej} = \vec{P}\cdot \vec{n} = P = \frac{(\varepsilon-\varepsilon_0)Q}{4\pi\varepsilon b^2}.\]Na vnitřním povrchu je vázaný náboj záporný — to je logické, neboť kladný náboj na kovové sféře jej „přitahuje“ k sobě.
Komentář
Celkový vázaný náboj Qb musí být nulový, což lze jednoduše ověřit výpočtem
\[Q_b = \sigma_\mathrm{b,vnitr}\,\cdot\, (4\pi a^2) + \sigma_\mathrm{b,vnej}\,\cdot\,(4\pi b^2) = 0.\]Odpověď
Potenciál ve středu koule je
\[\varphi(0) = \frac{Q}{4\pi}\left(\frac{1}{\varepsilon_0b}+\frac{1}{\varepsilon a}-\frac{1}{\varepsilon b}\right).\]Hustota objemového vázaného náboje v dielektriku je nulová.
Pro hustotu povrchového náboje na vnitřním povrchu platí
\[\sigma_{\mathrm{b,vnitr}} = -\frac{(\varepsilon-\varepsilon_0)Q}{4\pi\varepsilon a^2}\]a na vnějším povrchu platí
\[\sigma_{\mathrm{b,vnej}} = \frac{(\varepsilon-\varepsilon_0)Q}{4\pi\varepsilon b^2}.\]

