Sbírka řešených úloh

Diferenciální operátory ve sférických souřadnicích

Úloha číslo: 262

Sférické souřadnice (r, θ, φ) bodu P jsou definovány následovně: r je vzdálenost od počátku vztažné soustavy. Souřadnice θ je orientovaný úhel, který svírá spojnice bodu P a počátku s osou z, přičemž jej měříme od osy z. A souřadnice φ je úhel, který měříme od kladné poloosy x do přímky, kterou určuje počátek a průmět bodu P do roviny xy.

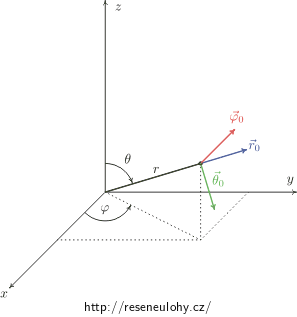
Vztah sférických a kartézských souřadnic popisují rovnice

\[x = r\,\sin\theta\,\cos\varphi,\] \[y = r\,\sin\theta\,\sin\varphi,\] \[z = r\,\cos\theta.\]

Ve sférických souřadnicích definujeme tři jednotkové vektory

\[\vec r_0, \vec \theta_0, \vec \varphi_0\]

mířící ve „směru růstu jednotlivých souřadnic“. Jestliže označíme jednotkové vektory v kartézské soustavě mířící po pořadě ve směru kladných poloos x, y, z postupně

\[\vec x_0, \vec y_0, \vec z_0\]

potom formálně můžeme jednotkové vektory ve sférických souřadnicích definovat vztahy

\[\vec r_0 = \sin\theta\,\cos\varphi\,\vec x_0 + \sin\theta\,\sin\varphi\,\vec y_0 + \cos\theta\,\vec z_0,\] \[\vec \theta_0 = \cos\theta\,\cos\varphi\,\vec x_0 + \cos\theta\,\sin\varphi\,\vec y_0 - \sin\theta\,\vec z_0,\] \[\vec \varphi_0 = -\sin\varphi\,\vec x_0 + \cos\varphi\,\vec y_0.\]

 

(a) Ověřte, že vektory \[\vec r_0,\ \vec\theta_0,\ \vec\varphi_0\] mají jednotkovou velikost a jsou navzájem kolmé.

(b) Ukažte, že gradient skalárního pole T má ve sférických souřadnicích tvar

\[\nabla T = \frac{\partial T}{\partial r}\vec r_0 + \frac{1}{r}\frac{\partial T}{\partial \theta}\vec \theta_0 + \frac{1}{r\sin\theta}\frac{\partial T}{\partial \varphi}\vec \varphi_0.\]

(c) Ukažte, že divergence vektorového pole \(\vec v\) má tvar

\[\nabla\cdot\vec v = \frac{1}{r^2}\frac{\partial}{\partial r}(r^2v_r)+\frac{1}{r\sin\theta}\frac{\partial}{\partial\theta}(\sin\theta\,v_\theta)+\frac{1}{r\sin\theta}\frac{\partial v_\varphi}{\partial \varphi}.\]

(d) Ukažte, že rotace vektorového pole \(\vec v\) má tvar

\[\nabla\times\vec v = \frac{1}{r\sin\theta}\left[\frac{\partial}{\partial \theta}(\sin\theta\,v_\varphi)-\frac{\partial v_\theta}{\partial \varphi}\right]\,\vec r_0 + \frac{1}{r}\left[\frac{1}{\sin\theta}\frac{\partial v_r}{\partial \varphi\varphi}-\frac{\partial}{\partial r}(rv_\varphi)\right]\,\vec \theta_0 + \frac{1}{r}\left[\frac{\partial}{\partial r}(rv_\theta)-\frac{\partial v_r}{\partial \theta}\right]\,\vec \varphi_0.\]

• Rozbor

  Úlohu budeme řešit přímým výpočtem.

  S výjimkou části (a), kterou lze vyřešit přímočarým počítáním, máme v ostatních částech úlohy převádět různé diferenciální operátory. K tomu potřebujeme zvládnout:

  • vyjádření parciální derivace podle kartézských souřadnic pomocí parciálních derivací podle sférických souřadnic,
  • výpočet složek vektoru ve sférických souřadnicích z jeho složek v souřadnicích kartézských.

  Podrobnosti jsou v nápovědách níže.

• Komentář – k vyjádření „sférických“ jednotkových vektorů

  Asi nejnázornější cestou, jak tyto vektory vyjádřit, je využít geometrie. Tady poukážeme na způsob, jak k nim dojít na základě ryze početních úvah.

  V jakýchkoli souřadnicích definujeme základní jednotkové vektory tak, aby mířili ve směru přírůstku jednotlivých souřadnic. V kartézské soustavě tedy míří ve směru kladných poloos x, y, z.

  Má-li být stejná konvence dodržena také u sférických souřadnic, pak musí platit, že jednotkové vektory \(\vec r_0,\,\vec\theta_0,\,\vec\varphi_0\) musí mít směr přírůstku souřadnic r, θ, φ. To jest, popořadě musí mít směr vektorů

  \[\frac{\partial\vec r}{\partial r}, \quad \frac{\partial\vec r}{\partial \theta}, \quad \frac{\partial\vec r}{\partial \varphi},\]

  kde \(\vec r\) je polohový vektor. V kartézských souřadnicích samozřejmě platí, že

  \[\vec r = (x,y,z),\]

  neboli v jiném zápisu

  \[\vec r = x\vec x_0 + y\vec y_0 + z\vec z_0.\]

  Nyní využijeme definičních vztahů sférických souřadnic a dosazením za x, y, z dostaneme, že

  \[\vec r = r\,\sin\,\theta\,\cos\,\varphi\, \vec x_0 + r\,\sin\,\theta\,\sin\,\varphi\,\vec y_0 + r\,\cos\,\theta\,\vec z_0.\]

  Nyní vypočteme hledané derivace (uvědomte si, že vektory \(\vec x_0, \, \vec y_0, \, \vec z_0\) jsou konstantní)

  \[\frac{\partial\vec r}{\partial r} = \sin\,\theta\,\cos\,\varphi\, \vec x_0 + \sin\,\theta\,\sin\,\varphi\,\vec y_0 + \cos\,\theta\,\vec z_0,\] \[\frac{\partial\vec r}{\partial \theta} = r\,\cos\,\theta\,\cos\,\varphi\, \vec x_0 + r\,\cos\,\theta\,\sin\,\varphi\,\vec y_0 - r\,\sin\,\theta\,\vec z_0,\] \[\frac{\partial\vec r}{\partial \varphi} = -r\,\sin\,\theta\,\sin\,\varphi\, \vec x_0 + r\,\sin\,\theta\,\cos\,\varphi\,\vec y_0.\]

  Nyní stačí tyto tři vektory podělit jejich velikostí. Protože platí (podle Pythagorovy věty pro vektorovou algebru, neboť „kartézské“ vektory jsou jednotkové a na sebe kolmé)

  \[\left|\frac{\partial\vec r}{\partial r}\right|^2 = \sin^2\theta\,\cos^2\varphi + \sin^2\theta\,\sin^2\varphi + \cos^2\theta = 1,\] \[\left|\frac{\partial\vec r}{\partial \theta}\right|^2 = r^2\,\cos^2\theta\,\cos^2\varphi + r^2\,\cos^2\theta\,\sin^2\varphi + r^2\,\sin^2\theta = r^2,\] \[\left|\frac{\partial\vec r}{\partial \varphi}\right|^2 = r^2\,\sin^2\theta\,\sin^2\varphi + r^2\,\sin^2\theta\,\cos^2\varphi = r^2\sin^2\theta,\]

  dostáváme, že

  \[\vec r_0 = \frac{\frac{\partial\vec r}{\partial r}}{|\frac{\partial\vec r}{\partial r}|} = \sin\,\theta\,\cos\,\varphi\, \vec x_0 + \sin\,\theta\,\sin\,\varphi\,\vec y_0 + \cos\,\theta\,\vec z_0,\] \[\vec \theta_0 = \frac{\frac{\partial\vec r}{\partial \theta}}{|\frac{\partial\vec r}{\partial \theta}|} = \cos\,\theta\,\cos\,\varphi\, \vec x_0 + \cos\,\theta\,\sin\,\varphi\,\vec y_0 - \sin\,\theta\,\vec z_0,\] \[\vec \varphi_0 = \frac{\frac{\partial\vec r}{\partial \varphi}}{|\frac{\partial\vec r}{\partial \varphi}|} = -\sin\,\varphi\, \vec x_0 + \cos\,\varphi\,\vec y_0.\]

• Řešení části (a)

  Nejprve ověříme, že vektory \(\vec r_0, \ \vec\theta_0, \ \vec\varphi_0\) jsou jednotkové. K tomu využijeme, že „kartézské“ jednotkové vektory \(\vec x_0,\ \vec y_0,\ \vec z_0\) jsou jednotkové a na sebe kolmé. To znamená, že

  \[\vec x_0\cdot \vec x_0 = 1, \quad \vec y_0\cdot\vec y_0 = 1, \quad \vec z_0\cdot \vec z_0 = 1\] \[\vec x_0\cdot \vec y_0 = 0, \quad \vec x_0\cdot\vec z_0 = 0, \quad \vec y_0\cdot \vec z_0 = 0.\]

  Díky těmto vztahům dostáváme (podle Pythagorovy věty pro vektorovou algebru), že

  \[|\vec r_0|^2 = \vec r_0\cdot\vec r_0 =\] \[=(\sin\,\theta\,\cos\,\varphi)^2 + (\sin\,\theta\,\sin\,\varphi)^2 + (\cos\,\theta)^2 = \sin^2\theta\,(\sin^2\varphi+\cos^2\varphi) + \cos^2\theta = \sin^2\theta + \cos^2\theta = 1.\]

  Obdobně platí

  \[|\vec \theta_0|^2 = \vec \theta_0\cdot\vec \theta_0=\] \[= (\cos\,\theta\,\cos\,\varphi)^2 + (\cos\,\theta\,\sin\,\varphi)^2 + (\sin\,\theta)^2 = \cos^2\theta\,(\sin^2\varphi+\cos^2\varphi) + \sin^2\theta = \cos^2\theta + \sin^2\theta = 1.\]

  A zcela analogicky také

  \[|\vec \varphi_0|^2 = \vec \varphi_0\cdot\vec \varphi_0 = (-\sin\,\theta)^2 + (\cos\,\theta)^2 = 1.\]

  Nyní ověříme kolmost dvojic různých vektorů \(\vec r_0,\ \vec \theta_0, \ \vec\varphi_0\). K tomu stačí spočítat jejich skalární součin

  \[\vec r_0 \cdot \vec \theta_0 = (\sin\,\theta\,\cos\,\theta\,\cos^2\varphi)+(\sin\,\theta\,\cos\,\theta\,\sin^2\varphi)-(\sin\,\theta\,\cos\,\theta) = \sin\,\theta\,\cos\,\theta\,(\cos^2\varphi+\sin^2\varphi-1) = 0.\]

  Obdobně je

  \[\vec r_0 \cdot \vec \varphi_0 = -(\sin\,\theta\,\cos\,\varphi\,\sin\,\varphi)+(\sin\,\theta\,\sin\,\varphi\,\cos\,\varphi) + 0 = 0\]

  a také platí

  \[\vec \theta_0 \cdot \vec \varphi_0 = -(\cos\,\theta\,\cos\,\varphi\,\sin\,\varphi)+(\cos\,\theta\,\sin\,\varphi\,\cos\,\varphi) + 0 = 0.\]

• Vyjádření kartézských jednotkových vektorů pomocí sférických

  Ukažte, že platí

  \[\vec x_0 = \sin\,\theta\,\cos\,\varphi\,\vec r_0 + \cos\,\theta\,\cos\,\varphi\,\vec \theta_0 - \sin\,\varphi\,\vec\varphi_0\] \[\vec y_0 = \sin\,\theta\,\sin\,\varphi\,\vec r_0 + \cos\,\theta\,\sin\,\varphi\,\vec \theta_0 + \cos\,\varphi\,\vec\varphi_0\] \[\vec z_0 = \cos\,\theta\,\vec r_0 -\sin\,\theta\,\vec\theta_0.\]

• Vyjádření kartézských jednotkových vektorů – řešení

  Nyní najdeme vyjádření jednotkových vektorů \(\vec x_0,\, \vec y_0,\, \vec z_0\) pomocí vektorů \(\vec r_0,\,\vec \theta_0,\, \vec \varphi_0\).

  Víme již, že platí

  \[\vec r_0 = \sin\,\theta\,\cos\,\varphi\,\vec x_0 + \sin\,\theta\,\sin\,\varphi\,\vec y_0 + \cos\,\theta\,\vec z_0\tag{A}\] \[\vec \theta_0 = \cos\,\theta\,\cos\,\varphi\,\vec x_0 + \cos\,\theta\,\sin\,\varphi\,\vec y_0 - \sin\,\theta\,\vec z_0\tag{B}\] \[\vec \varphi_0 = -\sin\,\theta\,\vec x_0 + \cos\,\theta\,\vec y_0.\tag{C}\]

  Nyní rovnici (A) vynásobíme členem \(\sin\,\theta\) a rovnici (B) členem \(\cos\,\theta\) a dostaneme

  \[\sin\,\theta\,\vec r_0 = \sin^2\theta\,\cos\,\varphi\,\vec x_0 + \sin^2\theta\,\sin\,\varphi\,\vec y_0 + \cos\,\theta\,\sin\,\theta\vec z_0\] \[\cos\,\theta\,\vec \theta_0 = \cos^2\theta\,\cos\,\varphi\,\vec x_0 + \cos^2\theta\,\sin\,\varphi\,\vec y_0 - \cos\,\theta\,\sin\,\theta\,\vec z_0.\]

  Rovnice sečteme a přidáme rovnici (C) pro \(\vec\varphi_0\)

  \[\sin\,\theta\,\vec r_0 + \cos\,\theta\,\vec\theta_0 = \cos\,\varphi\,\vec x_0 + \sin\,\varphi\,\vec y_0\tag{1}\] \[\vec \varphi_0 = -\sin\,\varphi\,\vec x_0 + \cos\,\varphi\,\vec y_0.\tag{2}\]

  Vynásobením (1) členem \(\cos\varphi\), (2) členem \(\sin\varphi\) a odečtením dostaneme

  \[\vec x_0 = \sin\,\theta\,\cos\,\varphi\,\vec r_0 + \cos\,\theta\,\cos\,\varphi\,\vec \theta_0 - \sin\,\varphi\,\vec\varphi_0.\]

  Vynásobením (1) členem \(\sin\varphi\), (2) členem \(\cos\varphi\) a sečtením dostaneme

  \[\vec y_0 = \sin\,\theta\,\sin\,\varphi\,\vec r_0 + \cos\,\theta\,\sin\,\varphi\,\vec \theta_0 + \cos\,\varphi\,\vec\varphi_0.\]

  Konečně poslední vektor \(\vec z_0\) dostaneme takto: rovnici (A) vynásobíme členem \(\cos\,\theta\)

  a rovnici (B) členem \(\sin\,\theta\)

  \[\cos\theta\,\vec r_0 = \sin\,\theta\,\cos\,\varphi\,\cos\,\theta\,\vec x_0 + \sin\,\theta\,\sin\,\varphi\,\cos\,\theta\,\vec y_0 + \cos^2\theta\,\vec z_0\] \[\sin\theta\,\vec \theta_0 = \cos\,\theta\,\cos\,\varphi\,\sin\,\theta\,\vec x_0 + \cos\,\theta\,\sin\,\varphi\,\sin\,\theta\,\vec y_0 - \sin^2\theta\,\vec z_0,\]

  obě získané rovnice od sebe odečteme. Na pravé straně dostaneme vektor \(\vec z_0\) a proto platí

  \[\vec z_0 = \cos\,\theta\,\vec r_0 -\sin\,\theta\,\vec\theta_0.\]

• Sférické souřadnice vyjádřené pomocí kartézských souřadnic

  Ukažte, že platí

  \[r = \sqrt{x^2+y^2+z^2}\] \[\theta = \arccos\,\frac{z}{r}\] \[\varphi = \arctan\,\frac{y}{x}.\]

• Sférické souřadnice pomocí kartézských — řešení

  Umocněním definičních vztahů pro sférické souřadnice a jejich sečtením dostaneme

  \[x^2+y^2+z^2 = r^2(\sin^2\theta\cos^2\varphi + \sin^2\theta\sin^2\varphi + \cos^2\theta) = r^2,\]

  odkud ihned máme, že

  \[r = \sqrt{x^2+y^2+z^2}.\]

  Obdobně zřejmě platí, že

  \[\frac{z}{r} = \cos\theta \ \Rightarrow \ \theta = \arccos\,\frac{z}{r}.\]

  Nakonec máme, že

  \[\frac{y}{x} = \tan\varphi \ \Rightarrow \ \varphi = \arctan\,\frac{y}{x}.\]

• Výpočet parciálních derivací — shrnutí vztahů

  Pro další účely vypočtěte postupně parciální derivace proměnných r, θ, φ podle proměnných x, y, z (celkem devět derivací). K tomu použijte vyjádření r, θ, φ jako funkcí kartézských souřadnic.

  Nakonec tyto parciální derivace vyjádřete pomocí souřadnic sférických, to jest pomocí proměnných r,θ,φ.

  To jest, ukažte, že platí

  \[\frac{\partial r}{\partial x} = \sin\,\theta\,\cos\,\varphi\tag{a1}\] \[\frac{\partial r}{\partial y} = \sin\,\theta\,\sin\,\varphi\tag{a2}\] \[\frac{\partial r}{\partial z} = \cos\,\theta\tag{a3}\] \[ \frac{\partial \theta}{\partial x} = \frac{1}{r}\cos\varphi\cos\theta\tag{b1}\] \[ \frac{\partial \theta}{\partial y} = \frac{1}{r}\sin\varphi\cos\theta\tag{b2}\] \[ \frac{\partial \theta}{\partial z} = -\frac{1}{r}\sin\,\theta\tag{b3}\] \[\frac{\partial \varphi}{\partial x} = -\frac{1}{r\sin\theta}\sin\varphi\tag{c1}\] \[\frac{\partial \varphi}{\partial y} = \frac{1}{r\sin\theta}\cos\varphi\tag{c2}\] \[\frac{\partial \varphi}{\partial z} = 0.\tag{c3}\]

• Výpočet parciálních derivací

  Z vyjádření sférických souřadnic (r, θ, φ) pomocí kartézských souřadnic (x, y, z) – viz nápovědu výše – vypočteme příslušné parciální derivace.

  Pro proměnnou r platí, že

  \[r = \sqrt{x^2+y^2+z^2}.\]

  Odtud vyplývá

  \[\frac{\partial r}{\partial x} = \frac{x}{\sqrt{x^2+y^2+z^2}} = \frac{x}{r} = \sin\,\theta\,\cos\,\varphi\tag{a1}\] \[\frac{\partial r}{\partial y} = \frac{y}{\sqrt{x^2+y^2+z^2}} = \frac{y}{r} = \sin\,\theta\,\sin\,\varphi\tag{a2}\] \[\frac{\partial r}{\partial z} = \frac{z}{\sqrt{x^2+y^2+z^2}} = \frac{z}{r} = \cos\,\theta.\tag{a3}\]

  Pro proměnnou θ máme vztah

  \[\theta = \arccos\,\frac{z}{\sqrt{x^2+y^2+z^2}}.\]

  Odtud vyplývá

  \[\frac{\partial \theta}{\partial x} = -\frac{1}{\sqrt{1-\frac{z^2}{x^2+y^2+z^2}}}\cdot \frac{-1}{2}\frac{z\cdot 2x}{(x^2+y^2+z^2)^{3/2}} = \frac{x}{\sqrt{x^2+y^2}}\cdot \frac{z}{x^2+y^2+z^2} = \frac{x}{\sqrt{x^2+y^2}}\cdot \frac{z}{r^2} =\] \[= \frac{x}{\sqrt{x^2+y^2}}\cdot \frac{z}{r}\cdot \frac{1}{r}\]

  a odtud zpětným přepsáním do sférických souřadnic dostáváme vztah

  \[ \frac{\partial \theta}{\partial x} = \frac{1}{r}\cos\varphi\cos\theta.\tag{b1}\]

  Obdobně dostaneme

  \[ \frac{\partial \theta}{\partial y} = \frac{y}{\sqrt{x^2+y^2}}\cdot\frac{z}{r}\cdot\frac{1}{r}\] \[ \frac{\partial \theta}{\partial y} = \frac{1}{r}\sin\varphi\cos\theta\tag{b2}\]

  a nakonec

  \[ \frac{\partial \theta}{\partial z} = -\frac{1}{\sqrt{1-\frac{z^2}{x^2+y^2+z^2}}}\cdot \frac{\partial}{\partial z}\left(\frac{z}{\sqrt{x^2+y^2+z^2}}\right) = -\frac{\sqrt{x^2+y^2+z^2}}{\sqrt{x^2+y^2}}\cdot\frac{\sqrt{x^2+y^2+z^2}-z\cdot \frac{z}{\sqrt{x^2+y^2+z^2}}}{x^2+y^2+z^2} = \] \[= -\frac{1}{\sqrt{x^2+y^2}}\cdot\frac{x^2+y^2}{r^2} = -\frac{1}{x}\frac{x}{\sqrt{x^2+y^2}}\cdot \left(1-\frac{z^2}{r^2}\right),\]

  odkud zpětným dosazením sférických souřadnic získáme

  \[ \frac{\partial \theta}{\partial z} = -\frac{1}{r\sin\,\theta\,\cos\varphi}\cdot \cos\,\varphi\cdot \sin^2\theta = -\frac{1}{r}\sin\,\theta.\tag{b3}\]

  Nakonec pro proměnnou φ platí vztah

  \[\varphi = \arctan\,\frac{y}{x},\]

  odkud máme

  \[\frac{\partial \varphi}{\partial x} = \frac{1}{1+\frac{y^2}{x^2}}\cdot \left(-\frac{y}{x^2}\right) = -\frac{y}{x^2+y^2} = - \frac{1}{x}\cdot \frac{y}{\sqrt{x^2+y^2}} \cdot \frac{x}{\sqrt{x^2+y^2}}\]

  a zpětným převedením do sférických souřadnic dostaneme

  \[\frac{\partial \varphi}{\partial x} = -\frac{1}{r\sin\theta}\sin\varphi.\tag{c1}\]

  Obdobně máme

  \[\frac{\partial \varphi}{\partial y} = \frac{1}{1+\frac{y^2}{x^2}}\cdot \frac{1}{x} = \frac{x}{x^2+y^2} = \frac{1}{x}\cdot \frac{x}{\sqrt{x^2+y^2}} \cdot \frac{x}{\sqrt{x^2+y^2}}\]

  a zpětným převedením do sférických souřadnic dostaneme

  \[\frac{\partial \varphi}{\partial y} = \frac{1}{r\sin\theta}\cos\varphi.\tag{c2}\]

  Nakonec zřejmě platí

  odkud vyplývá

  \[\frac{\partial \varphi}{\partial z} = 0,\tag{c3}\]

  neboť θ jako funkce kartézských souřadnic na z nezávisí.

• Nápověda k části (b)

  Pro přepočítání parciálních derivací

  \[\frac{\partial T}{\partial x}, \quad \frac{\partial T}{\partial y}, \quad \frac{\partial T}{\partial z},\]

  použijte řetízkové pravidlo:

  \[\frac{\partial T}{\partial x} = \frac{\partial T}{\partial r}\frac{\partial r}{\partial x} + \frac{\partial T}{\partial \theta}\frac{\partial \theta}{\partial x} + \frac{\partial T}{\partial \varphi}\frac{\partial \varphi}{\partial x}\] \[\frac{\partial T}{\partial y} = \frac{\partial T}{\partial r}\frac{\partial r}{\partial y} + \frac{\partial T}{\partial \theta}\frac{\partial \theta}{\partial y} + \frac{\partial T}{\partial \varphi}\frac{\partial \varphi}{\partial y}\] \[\frac{\partial T}{\partial z} = \frac{\partial T}{\partial r}\frac{\partial r}{\partial z} + \frac{\partial T}{\partial \theta}\frac{\partial \theta}{\partial z} + \frac{\partial T}{\partial \varphi}\frac{\partial \varphi}{\partial z}\]

  a předchozích výsledků.

• Řešení části (b)

  Nechť T je skalární pole. V kartézských souřadnicích je jeho gradient definován jako vektorové pole

  \[\nabla T = \left(\frac{\partial T}{\partial x},\ \frac{\partial T}{\partial y},\ \frac{\partial T}{\partial z}\right),\]

  nebo můžeme také psát, že

  \[\nabla T = \frac{\partial T}{\partial x}\vec x_0 + \frac{\partial T}{\partial y}\vec y_0 + \frac{\partial T}{\partial z}\vec z_0.\]

  V tomto vyjádření použijeme řetízkové pravidlo

  \[\nabla T = \frac{\partial T}{\partial x}\vec x_0 + \frac{\partial T}{\partial y}\vec y_0 + \frac{\partial T}{\partial z}\vec z_0 =\left(\frac{\partial T}{\partial r}\frac{\partial r}{\partial x} + \frac{\partial T}{\partial \theta}\frac{\partial \theta}{\partial x} + \frac{\partial T}{\partial \varphi}\frac{\partial \varphi}{\partial x}\right)\,\vec x_0 +\] \[+ \left(\frac{\partial T}{\partial r}\frac{\partial r}{\partial y} + \frac{\partial T}{\partial \theta}\frac{\partial \theta}{\partial y} + \frac{\partial T}{\partial \varphi}\frac{\partial \varphi}{\partial y}\right)\, \vec y_0 + \left(\frac{\partial T}{\partial r}\frac{\partial r}{\partial z} + \frac{\partial T}{\partial \theta}\frac{\partial \theta}{\partial z} + \frac{\partial T}{\partial \varphi}\frac{\partial \varphi}{\partial z}\right)\, \vec z_0 =\]

  a posléze dosadíme za parciální derivace a jednotkové vektory z nápověd výše

  \[= \left(\frac{\partial T}{\partial r}\,\sin\,\theta\,\cos\,\varphi + \frac{\partial T}{\partial \theta}\,\frac{1}{r}\,\cos\,\theta\,\cos\,\varphi - \frac{\partial T}{\partial \varphi}\,\frac{1}{r\sin\theta}\,\sin\,\varphi\right) \,\cdot\,\left(\sin\,\theta\,\cos\,\varphi\,\vec r_0 + \cos\,\theta\,\cos\,\varphi\,\vec \theta_0 - \sin\,\varphi\,\vec\varphi_0\right) +\] \[+ \left(\frac{\partial T}{\partial r}\,\sin\,\theta\,\sin\,\varphi + \frac{\partial T}{\partial \theta}\,\frac{1}{r}\,\cos\,\theta\,\sin\,\varphi + \frac{\partial T}{\partial \varphi}\,\frac{1}{r\sin\theta}\,\cos\,\varphi\right) \,\cdot\,\left(\sin\,\theta\,\sin\,\varphi\,\vec r_0 + \cos\,\theta\,\sin\,\varphi\,\vec \theta_0 + \cos\,\varphi\,\vec\varphi_0\right) +\] \[+ \left(\frac{\partial T}{\partial r}\,\cos\,\theta - \frac{\partial T}{\partial \theta}\,\frac{1}{r}\,\sin\,\theta\right)\,\cdot\,\left(\cos\,\theta\,\vec r_0 -\sin\,\theta\,\vec\theta_0\right)\]

  a po úpravách dostaneme hledaný vztah

  \[\nabla T = \frac{\partial T}{\partial r}\vec r_0 + \frac{1}{r}\frac{\partial T}{\partial \theta}\vec \theta_0 + \frac{1}{r\sin\theta}\frac{\partial T}{\partial \varphi}\vec \varphi_0.\]

• Nápověda k části (c)

  Divergence vektorového pole \(\vec v\) je v kartézských souřadnicích definována vztahem

  \[\nabla\cdot\vec v = \frac{\partial v_x}{\partial x}+\frac{\partial v_y}{\partial y}+\frac{\partial v_z}{\partial z}.\]

  Nejprve použijeme řetízkového pravidla. Platí, že

  \[\frac{\partial v_x}{\partial x} = \frac{\partial v_x}{\partial r}\frac{\partial r}{\partial x} + \frac{\partial v_x}{\partial \theta}\frac{\partial \theta}{\partial x} + \frac{\partial v_x}{\partial \varphi}\frac{\partial \varphi}{\partial x}\] \[\frac{\partial v_y}{\partial y} = \frac{\partial v_y}{\partial r}\frac{\partial r}{\partial y} + \frac{\partial v_y}{\partial \theta}\frac{\partial \theta}{\partial y} + \frac{\partial v_y}{\partial \varphi}\frac{\partial \varphi}{\partial y}\] \[\frac{\partial v_z}{\partial z} = \frac{\partial v_z}{\partial r}\frac{\partial r}{\partial z} + \frac{\partial v_z}{\partial \theta}\frac{\partial \theta}{\partial z} + \frac{\partial v_z}{\partial \varphi}\frac{\partial \varphi}{\partial z}.\]

  A poté ještě musíme kartézské složky vektoru \(\vec v\) pomocí „sférických složek“ a sférických souřadnic.

  To provedeme tak, že do vyjádření

  \[\vec v = v_r\vec r_0 + v_\theta\vec \theta_0 + v_\varphi\vec \varphi_0\]

  nahradíme vektory \(\vec r_0, \, \vec \theta_0, \, \vec \varphi_0\) jejich vyjádřením pomocí kartézských souřadnic.

• Řešení části (c)

  Divergence vektorového pole \(\vec v\) je v kartézských souřadnicích definována vztahem

  \[\nabla\cdot\vec v = \frac{\partial v_x}{\partial x}+\frac{\partial v_y}{\partial y}+\frac{\partial v_z}{\partial z}.\]

  Nejprve použijeme řetízkového pravidla. Platí, že

  \[\frac{\partial v_x}{\partial x} = \frac{\partial v_x}{\partial r}\frac{\partial r}{\partial x} + \frac{\partial v_x}{\partial \theta}\frac{\partial \theta}{\partial x} + \frac{\partial v_x}{\partial \varphi}\frac{\partial \varphi}{\partial x}\] \[\frac{\partial v_y}{\partial y} = \frac{\partial v_y}{\partial r}\frac{\partial r}{\partial y} + \frac{\partial v_y}{\partial \theta}\frac{\partial \theta}{\partial y} + \frac{\partial v_y}{\partial \varphi}\frac{\partial \varphi}{\partial y}\] \[\frac{\partial v_z}{\partial z} = \frac{\partial v_z}{\partial r}\frac{\partial r}{\partial z} + \frac{\partial v_z}{\partial \theta}\frac{\partial \theta}{\partial z} + \frac{\partial v_z}{\partial \varphi}\frac{\partial \varphi}{\partial z}.\]

  A poté ještě musíme kartézské složky vektoru \(\vec v\) vyjádřit pomocí „složek sférických“ – tedy v_x, v_y a v_z vyjádřit pomocí sférických souřadnic a složek v_r, v_θ a v_φ.

  Nejprve ve vyjádření

  \[\vec v = v_r\vec r_0 + v_\theta\vec \theta_0 + v_\varphi\vec \varphi_0\]

  nahradíme sférické jednotkové vektory kartézskými podle vztahů uvedených v zadání úlohy

  \[\vec r_0 = \sin\theta\,\cos\varphi\,\vec x_0 + \sin\theta\,\sin\varphi\,\vec y_0 + \cos\theta\,\vec z_0\] \[\vec \theta_0 = \cos\theta\,\cos\varphi\,\vec x_0 + \cos\theta\,\sin\varphi\,\vec y_0 - \sin\theta\,\vec z_0\] \[\vec \varphi_0 = -\sin\varphi\,\vec x_0 + \cos\varphi\,\vec y_0.\]

  Dostaneme tak, že

  \[\vec v = \left(v_r\sin\theta\,\cos\varphi + v_\theta\cos\theta\,\cos\varphi-v_\varphi\sin\varphi\right)\vec x_0 +\left(v_r\sin\theta\,\sin\varphi + v_\theta\cos\theta\,\sin\varphi + v_\varphi\cos\varphi\right)\vec y_0 + \] \[+\left(v_r\cos\theta -v_\theta\sin\theta\right)\vec z_0.\]

  Porovnáním se vztahem

  \[\vec v = v_x\vec x_0 + v_y\vec y_0 + v_z\vec z_0\]

  dostaneme, že

  \[v_x = v_r\sin\theta\,\cos\varphi + v_\theta\cos\theta\,\cos\varphi-v_\varphi\sin\varphi\] \[v_y = v_r\sin\theta\,\sin\varphi + v_\theta\cos\theta\,\sin\varphi + v_\varphi\cos\varphi\] \[v_z = v_r\cos\theta -v_\theta\sin\theta.\]

  Kombinací řetízkového pravidla, parciálních derivací vypočtených v nápovědě výše a právě odvozených vztahů dostaneme:

  \[\frac{\partial v_x}{\partial x} = \frac{\partial v_x}{\partial r}\frac{\partial r}{\partial x} + \frac{\partial v_x}{\partial \theta}\frac{\partial \theta}{\partial x} + \frac{\partial v_x}{\partial \varphi}\frac{\partial \varphi}{\partial x} =\] \[ = \frac{\partial}{\partial r}\left(v_r\sin\theta\,\cos\varphi + v_\theta\cos\theta\,\cos\varphi-v_\varphi\sin\varphi\right) \cdot (\sin\theta\cos\varphi) +\] \[+ \frac{\partial}{\partial \theta}\left(v_r\sin\theta\,\cos\varphi + v_\theta\cos\theta\,\cos\varphi-v_\varphi\sin\varphi\right) \cdot \frac{1}{r}\cos\theta\cos\varphi +\] \[+ \frac{\partial}{\partial \varphi}\left(v_r\sin\theta\,\cos\varphi + v_\theta\cos\theta\,\cos\varphi-v_\varphi\sin\varphi\right)\cdot \left(-\frac{1}{r\sin\theta}\sin\varphi\right) =\]

  a nyní je potřeba provést derivování

  \[= \frac{\partial v_r}{\partial r}\sin^2\theta\cos^2\varphi + \frac{\partial v_\theta}{\partial r}\sin\theta\,\cos\theta\,\cos^2\varphi - \frac{\partial v_\varphi}{\partial r}\sin\theta\,\sin\varphi\,\cos\varphi +\] \[+ \frac{1}{r}\frac{\partial v_r}{\partial\theta}\cos\theta\,\sin\theta\,\cos^2\varphi + \frac{1}{r}v_r\cos^2\theta\cos^2\varphi +\] \[+ \frac{1}{r}\frac{\partial v_\theta}{\partial \theta}\cos^2\theta\cos^2\varphi - \frac{1}{r}v_\theta\sin\theta\,\cos\theta\,\cos^2\varphi -\frac{1}{r}\frac{\partial v_\varphi}{\partial\theta}\cos\theta\,\sin\varphi\,\cos\varphi - \] \[- \frac{1}{r}\frac{\partial v_r}{\partial\varphi}\cos\varphi\sin\varphi + \frac{1}{r}v_r\sin^2\varphi - \frac{1}{r\sin\theta}\frac{\partial v_\theta}{\partial\varphi}\cos\theta\,\cos\varphi\,\sin\varphi +\] \[+ \frac{1}{r\sin\theta}v_\theta\cos\theta\,\sin^2\varphi + \frac{1}{r\sin\theta}\frac{\partial v_\varphi}{\partial\varphi}\sin^2\varphi + \frac{1}{r\sin\theta}\,\cos\varphi\,\sin\varphi.\]

  Obdobně vypočteme y-ový člen:

  \[\frac{\partial v_y}{\partial y}= \frac{\partial v_y}{\partial r}\frac{\partial r}{\partial y} + \frac{\partial v_y}{\partial \theta}\frac{\partial \theta}{\partial y} + \frac{\partial v_y}{\partial \varphi}\frac{\partial \varphi}{\partial y} =\] \[ = \frac{\partial}{\partial r}\left(v_r\sin\theta\,\sin\varphi + v_\theta\cos\theta\,\sin\varphi+v_\varphi\cos\varphi\right) \cdot (\sin\theta\sin\varphi) +\] \[+ \frac{\partial}{\partial \theta}\left(v_r\sin\theta\,\sin\varphi + v_\theta\cos\theta\,\sin\varphi+v_\varphi\cos\varphi\right) \cdot \frac{1}{r}\cos\theta\sin\varphi +\] \[+ \frac{\partial}{\partial \varphi}\left(v_r\sin\theta\,\sin\varphi + v_\theta\cos\theta\,\sin\varphi+v_\varphi\cos\varphi\right)\cdot \left(\frac{1}{r\sin\theta}\cos\varphi\right) =\]

  a nyní je potřeba provést derivování

  \[= \frac{\partial v_r}{\partial r}\sin^2\theta\sin^2\varphi + \frac{\partial v_\theta}{\partial r}\sin\theta\,\cos\theta\,\sin^2\varphi + \frac{\partial v_\varphi}{\partial r}\sin\theta\,\sin\varphi\,\cos\varphi +\] \[+ \frac{1}{r}\frac{\partial v_r}{\partial\theta}\cos\theta\,\sin\theta\,\sin^2\varphi + \frac{1}{r}v_r\cos^2\theta\sin^2\varphi +\] \[+ \frac{1}{r}\frac{\partial v_\theta}{\partial \theta}\cos^2\theta\sin^2\varphi - \frac{1}{r}v_\theta\sin\theta\,\cos\theta\,\sin^2\varphi + \frac{1}{r}\frac{\partial v_\varphi}{\partial\theta}\cos\theta\,\sin\varphi\,\cos\varphi +\] \[+ \frac{1}{r}\frac{\partial v_r}{\partial\varphi}\sin\varphi\,\cos\varphi + \frac{1}{r}v_r\cos^2\varphi + \frac{1}{r\sin\theta}\frac{\partial v_\theta}{\partial\varphi}\cos\theta\,\sin\varphi\,\cos\varphi +\] \[+ \frac{1}{r\sin\theta}v_\theta\cos\theta\,\cos^2\varphi + \frac{1}{r\sin\theta}\frac{\partial v_\varphi}{\partial\varphi}\cos^2\varphi - \frac{1}{r\sin\theta}v_\varphi\,\sin\varphi\,\cos\varphi .\]

  A nakonec vypočteme z-ový člen:

  \[\frac{\partial v_z}{\partial z}= \frac{\partial v_z}{\partial r}\frac{\partial r}{\partial z} + \frac{\partial v_z}{\partial \theta}\frac{\partial \theta}{\partial z} + \frac{\partial v_z}{\partial \varphi}\frac{\partial \varphi}{\partial z} = \frac{\partial}{\partial r}\left(v_r\cos\theta -v_\theta\sin\theta\right) \cdot \cos\theta + \frac{\partial}{\partial \theta}\left(v_r\cos\theta -v_\theta\sin\theta\right) \cdot \left(-\frac{1}{r}\sin\theta\right) =\]

  a nyní je potřeba provést derivování

  \[= \frac{\partial v_r}{\partial r}\cos^2\theta - \frac{\partial v_\theta}{\partial r}\sin\theta\,\cos\theta + \frac{1}{r}\frac{\partial v_r}{\partial\theta}\cos\theta\,\sin\theta + \frac{1}{r}v_r\sin^2\theta + \frac{1}{r}\frac{\partial v_\theta}{\partial \theta}\sin^2\theta + \frac{1}{r}v_\theta\sin\theta\,\cos\theta.\]

  Sečtením všech předchozích vztahů dostaneme

  \[\nabla \cdot \vec v = \frac{\partial v_r}{\partial r} + \frac{2}{r}v_r + \frac{1}{r}\frac{\partial v_\theta}{\partial\theta} + \frac{1}{r\sin\theta}v_\theta\cos\theta + \frac{1}{r\sin\theta}\frac{\partial v_\varphi}{\partial\varphi}.\]

  S přihlédnutím ke vztahům

  \[\frac{1}{r^2}\frac{\partial}{\partial r}(r^2v_r) = \frac{2}{r}v_r + \frac{\partial v_r}{\partial r}\]

  a

  \[\frac{\partial}{\partial\theta}(v_\theta\sin\theta) = v_\theta\cos\theta + \frac{\partial v_\theta}{\partial\theta}\sin\theta\]

  ihned dostáváme hledaný vztah.

• Nápověda k části (d)

  Rotace v kartézských souřadnicích je vektor, který značíme \(\nabla\times\vec v\) a jehož složky jsou definovány následovně:

  \[(\nabla\times\vec v)_x = \frac{\partial v_z}{\partial y} - \frac{\partial v_y}{\partial z}\] \[(\nabla\times\vec v)_y = \frac{\partial v_x}{\partial z} - \frac{\partial v_z}{\partial x}\] \[(\nabla\times\vec v)_z = \frac{\partial v_y}{\partial x} - \frac{\partial v_x}{\partial y}.\]

  Naším úkolem je najít složky tohoto vektoru ve sférických souřadnicích a jednotlivé členy vyjádřit pomocí složek vektoru \(\vec v\) ve sférických souřadnicích – ot jest pomocí v_r, v_θ a v_φ – a jejich derivací podle sférických souřadnic.

  Začneme tak, že složky \((\nabla\times\vec v)_{x,y,z}\) vyjádříme pomocí sférických souřadnic vektoru \(\vec v\) a jejich derivací podle sférických souřadnic. K tomu použijeme řetízkové pravidlo a již výše spočtené parciální derivace.

  Poté použijeme následující postup. Jestliže libovolný vektor \(\vec u\) má souřadnice (u_x, u_y, u_z), pak jej lze psát ve tvaru

  \[\vec u = u_x\vec x_0 + u_y\vec y_0 + u_z\vec z_0\]

  a dosazením za jednotkové kartézské vektory jejich vyjádřením pomocí sférických jednotkových vektorů umíme získat souřadnice vektoru \(\vec u\) ve sférických souřadnicích.

• Řešení části (d)

  Složky vektoru rotace mají tvar

  \[(\nabla\times\vec v)_x = \frac{\partial v_z}{\partial y} - \frac{\partial v_y}{\partial z}\] \[(\nabla\times\vec v)_y = \frac{\partial v_x}{\partial z} - \frac{\partial v_z}{\partial x}\] \[(\nabla\times\vec v)_z = \frac{\partial v_y}{\partial x} - \frac{\partial v_x}{\partial y}.\]

  Tyto parciální derivace vyjádříme pomocí sférických souřadnic.

  Z předchozí části (c) víme, že platí

  \[ v_x = v_r\sin\theta\,\cos\varphi + v_\theta\cos\theta\,\cos\varphi-v_\varphi\sin\varphi\] \[v_y = v_r\sin\theta\,\sin\varphi + v_\theta\cos\theta\,\sin\varphi + v_\varphi\cos\varphi\] \[v_z = v_r\cos\theta -v_\theta\sin\theta.\]

  z-ová složka rotace

  Podle řetízkového pravidla pak máme

  \[\frac{\partial v_x}{\partial y} = \frac{\partial v_x}{\partial r}\frac{\partial r}{\partial y} + \frac{\partial v_x}{\partial \theta}\frac{\partial \theta}{\partial y} + \frac{\partial v_x}{\partial \varphi}\frac{\partial \varphi}{\partial y} = ,\]

  nyní dosadíme z předchozích vztahů pro složku v_x a příslušné parciální derivace (viz nápověda výše)

  \[= \frac{\partial}{\partial r}\left(v_r\sin\theta\,\cos\varphi + v_\theta\cos\theta\,\cos\varphi-v_\varphi\sin\varphi\right)\cdot(\sin\theta\,\sin\varphi) +\] \[+ \frac{\partial}{\partial \theta}\left(v_r\sin\theta\,\cos\varphi + v_\theta\cos\theta\,\cos\varphi-v_\varphi\sin\varphi\right)\cdot\left(\frac{1}{r}\sin\varphi\,\cos\theta\right) +\] \[+ \frac{\partial}{\partial \varphi}\left(v_r\sin\theta\,\cos\varphi + v_\theta\cos\theta\,\cos\varphi-v_\varphi\sin\varphi\right)\cdot\left(\frac{1}{r\sin\theta}\cos\varphi\right).\]

  Znovu podle řetízkového pravidla můžeme psát

  \[\frac{\partial v_y}{\partial x} = \frac{\partial v_y}{\partial r}\frac{\partial r}{\partial x} + \frac{\partial v_y}{\partial \theta}\frac{\partial \theta}{\partial x} + \frac{\partial v_y}{\partial \varphi}\frac{\partial \varphi}{\partial x} = ,\]

  nyní dosadíme z předchozích vztahů pro složku v_y a příslušné parciální derivace (viz nápověda výše)

  \[= \frac{\partial}{\partial r}\left(v_r\sin\theta\,\sin\varphi + v_\theta\cos\theta\,\sin\varphi+v_\varphi\cos\varphi\right)\cdot(\sin\theta\,\cos\varphi) +\] \[+ \frac{\partial}{\partial \theta}\left(v_r\sin\theta\,\sin\varphi + v_\theta\cos\theta\,\sin\varphi+v_\varphi\cos\varphi\right)\cdot\left(\frac{1}{r}\cos\varphi\,\cos\theta\right) +\] \[+ \frac{\partial}{\partial \varphi}\left(v_r\sin\theta\,\sin\varphi + v_\theta\cos\theta\,\sin\varphi+v_\varphi\cos\varphi\right)\cdot\left(-\frac{1}{r\sin\theta}\sin\varphi\right).\]

  Využitím předchozím vztahů dostaneme po úpravách, že

  \[(\nabla\times \vec v)_z = \frac{\partial v_y}{\partial x}-\frac{\partial v_x}{\partial y} =\] \[= \frac{\partial v_\varphi}{\partial r}\sin\theta + \frac{1}{r}\frac{\partial v_\varphi}{\partial\theta}\cos\theta - \frac{1}{r}\frac{\partial v_r}{\partial\varphi} - \frac{1}{r\sin\theta}\frac{\partial v_r}{\partial\varphi}\cos\theta - \frac{1}{r\sin\theta}\frac{\partial v_\theta}{\partial\varphi}\cos\theta + \frac{1}{r\sin\theta}v_\varphi.\tag{R1}\]

  y-ová složka rotace

  Podle řetízkového pravidla pak máme

  \[\frac{\partial v_z}{\partial x} = \frac{\partial v_z}{\partial x}\frac{\partial r}{\partial x} + \frac{\partial v_z}{\partial \theta}\frac{\partial \theta}{\partial x} + \frac{\partial v_z}{\partial \varphi}\frac{\partial \varphi}{\partial x} = ,\]

  nyní dosadíme z předchozích vztahů pro složku v_z a příslušné parciální derivace (viz nápověda výše)

  \[= \frac{\partial}{\partial r}\left(v_r\cos\theta - v_\theta\sin\theta\right)\cdot(\sin\theta\,\cos\varphi) +\] \[+ \frac{\partial}{\partial \theta}\left(v_r\cos\theta - v_\theta\sin\theta\right)\cdot\left(\frac{1}{r}\cos\varphi\,\cos\theta\right) +\] \[+ \frac{\partial}{\partial \varphi}\left(v_r\cos\theta - v_\theta\sin\theta\right)\cdot\left(-\frac{1}{r\sin\theta}\sin\varphi\right).\]

  Znovu podle řetízkového pravidla můžeme psát

  \[\frac{\partial v_x}{\partial z} = \frac{\partial v_x}{\partial r}\frac{\partial r}{\partial z} + \frac{\partial v_x}{\partial \theta}\frac{\partial \theta}{\partial z} + \frac{\partial v_x}{\partial \varphi}\frac{\partial \varphi}{\partial z} =, \]

  nyní dosadíme z předchozích vztahů pro složku v_x a příslušné parciální derivace (viz nápověda výše)

  \[= \frac{\partial}{\partial r}\left(v_r\sin\theta\,\cos\varphi + v_\theta\cos\theta\,\cos\varphi-v_\varphi\sin\varphi\right)\cdot(\cos\theta) +\] \[+ \frac{\partial}{\partial \theta}\left(v_r\sin\theta\,\cos\varphi + v_\theta\cos\theta\,\cos\varphi-v_\varphi\sin\varphi\right)\cdot\left(-\frac{1}{r}\,\sin\theta\right) + 0.\]

  Využitím obou předchozích vztahů dostaneme, že

  \[(\nabla\times \vec v)_y = \frac{\partial v_x}{\partial z}-\frac{\partial v_z}{\partial x} =\] \[ =\frac{\partial v_\theta}{\partial r}\cos\varphi - \frac{\partial v_\varphi}{\partial r}\sin\varphi\cos\theta - \frac{1}{r}\frac{\partial v_r}{\partial \theta}\cos\varphi + \frac{1}{r}v_\theta\cos\varphi +\tag{R2}\] \[+ \frac{1}{r}\frac{\partial v_\varphi}{\partial \theta}\sin\theta\,\sin\varphi + \frac{1}{r\sin\theta}\frac{\partial v_r}{\partial \varphi}\cos\theta\sin\varphi - \frac{1}{r}\frac{\partial v_\theta}{\partial \varphi}\sin\varphi.\]

  x-ová složka rotace

  Podle řetízkového pravidla pak máme

  \[\frac{\partial v_y}{\partial z} = \frac{\partial v_y}{\partial r}\frac{\partial r}{\partial z} + \frac{\partial v_y}{\partial \theta}\frac{\partial \theta}{\partial z} + \frac{\partial v_y}{\partial \varphi}\frac{\partial \varphi}{\partial z} = ,\]

  nyní dosadíme z předchozích vztahů pro složku v_z a příslušné parciální derivace (viz nápověda výše)

  \[= \frac{\partial}{\partial r}\left(v_r\sin\theta\,\sin\varphi + v_\theta\cos\theta\,\sin\varphi + v_\varphi\cos\varphi\right)\cdot(\cos\theta) +\] \[+ \frac{\partial}{\partial \theta}\left(v_r\sin\theta\,\sin\varphi + v_\theta\cos\theta\,\sin\varphi + v_\varphi\cos\varphi\right)\cdot\left(-\frac{1}{r}\sin\theta\right) + 0.\]

  Znovu podle řetízkového pravidla můžeme psát

  \[\frac{\partial v_z}{\partial y} = \frac{\partial v_z}{\partial r}\frac{\partial r}{\partial y} + \frac{\partial v_z}{\partial \theta}\frac{\partial \theta}{\partial y} + \frac{\partial v_z}{\partial \varphi}\frac{\partial \varphi}{\partial y} = ,\]

  nyní dosadíme z předchozích vztahů pro složku v_x a příslušné parciální derivace (viz nápověda výše)

  \[= \frac{\partial}{\partial r}\left(v_r\cos\theta -v_\theta\sin\theta\right)\cdot(\sin\theta\,\sin\varphi) +\] \[+ \frac{\partial}{\partial \theta}\left(v_r\cos\theta -v_\theta\sin\theta\right)\cdot\left(\frac{1}{r}\sin\varphi\,\cos\theta\right) + \] \[+ \frac{\partial}{\partial \varphi}\left(v_r\cos\theta -v_\theta\sin\theta\right)\cdot\left(\frac{1}{r\sin\theta}\cos\varphi\right).\]

  Využitím obou předchozích vztahů dostaneme, že

  \[(\nabla\times \vec v)_x = \frac{\partial v_z}{\partial y}-\frac{\partial v_y}{\partial z} =\] \[ = -\frac{\partial v_\theta}{\partial r}\sin\varphi -\frac{\partial v_\varphi}{\partial r}\cos\varphi\,\cos\theta + \frac{1}{r}\frac{\partial v_r}{\partial \theta}\sin\varphi -\frac{1}{r}v_\theta\sin\varphi +\tag{R3}\] \[+ \frac{1}{r}\frac{\partial v_\varphi}{\partial \theta}\sin\theta\,\cos\varphi + \frac{1}{r\sin\theta}\frac{\partial v_r}{\partial \varphi}\cos\theta\,\cos\varphi - \frac{1}{r}\frac{\partial v_\theta}{\partial \varphi}\cos\varphi.\]

  Přepočet do sférických souřadnic

  Nyní ještě musíme přepočítat souřadnice vektoru rotace do sférických souřadnic. Obecně platí, že pokud má vektor \(\vec u\) souřadnice (u_x, u_y, u_z), potom lze psát

  \[\vec u = u_x\vec x_0 + u_y\vec y_0 + u_z\vec z_0\]

  a souřadnice (u_r, u_θ, u_φ) lze získat tak, že za vektory \(\vec x_0, \vec y_0, \vec z_0\) dosadíme jejich vyjádření pomocí vektorů \(\vec r_0, \vec \theta_0, \vec \varphi_0\) (viz výše). Platí, že

  \[\vec x_0 = \sin\,\theta\,\cos\,\varphi\,\vec r_0 + \cos\,\theta\,\cos\,\varphi\,\vec \theta_0 - \sin\,\varphi\,\vec\varphi_0\] \[\vec y_0 = \sin\,\theta\,\sin\,\varphi\,\vec r_0 + \cos\,\theta\,\sin\,\varphi\,\vec \theta_0 + \cos\,\varphi\,\vec\varphi_0\] \[\vec z_0 = \cos\,\theta\,\vec r_0 -\sin\,\theta\,\vec\theta_0.\]

  Dosazením do vztahu výše dostaneme, že

  \[\vec u = (u_x\sin\theta\,\cos\varphi + u_y\,sin\theta\,\sin\varphi + u_z\cos\theta)\vec r_0 + (u_x\cos\theta\,\cos\varphi + u_y\,cos\theta\,\sin\varphi - u_z\sin\theta)\vec \theta_0 +\] \[+ (-u_x\sin\varphi + u_y\,\cos\varphi)\vec \varphi_0,\]

  odkud ihned vyplývá, že

  \[u_r = u_x\sin\theta\,\cos\varphi + u_y\,sin\theta\,\sin\varphi + u_z\cos\theta\] \[u_\theta = u_x\cos\theta\,\cos\varphi + u_y\,cos\theta\,\sin\varphi - u_z\sin\theta\] \[u_\varphi = -u_x\sin\varphi + u_y\,\cos\varphi.\]

  Aplikací tohoto obecného vztahu na \(\vec u = (\nabla\times\vec v)\) dostaneme, že

  \[(\nabla\times\vec v)_r = (\nabla\times\vec v)_x\sin\theta\,\cos\varphi + (\nabla\times\vec v)_y\,sin\theta\,\sin\varphi + (\nabla\times\vec v)_z\cos\theta ,\]

  což s využitím vztahů (R1), (R2), (R3) výše dává po úpravě

  \[(\nabla\times\vec v)_r = \frac{1}{r}\frac{\partial v_\varphi}{\partial \theta} -\frac{1}{r\sin\theta}\frac{\partial v_\theta}{\partial \varphi} + \frac{1}{r\sin\theta}v_\varphi\cos\theta .\]

  Porovnejme dosažený vztah se vztahem uvedeným v zadání úlohy, z něhož plyne

  \[(\nabla\times\vec v)_r = \frac{1}{r\sin\theta}\left[\frac{\partial}{\partial \theta}(\sin\theta\,v_\varphi)-\frac{\partial v_\theta}{\partial\varphi}\right].\]

  Zjišťujeme, že po provedení derivace v hranaté závorce a roznásobení dostáváme tentýž vztah.

  Kýžené rovnosti pro ostatní složky vektoru rotace dostaneme analogicky dosazením (R1), (R2), (R3) do vztahů

  \[(\nabla\times\vec v)_\theta = (\nabla\times\vec v)_x\cos\theta\,\cos\varphi + (\nabla\times\vec v)_y\,cos\theta\,\sin\varphi - (\nabla\times\vec v)_z\sin\theta\] \[(\nabla\times\vec v)_\varphi = -(\nabla\times\vec v)_x\sin\varphi + (\nabla\times\vec v)_y\,\cos\varphi.\]

• Odpověď

  Ověřili jsme vztahy v zadání úlohy.