Nabitá úsečka 2
Úloha číslo: 275
Úsečka délky L je nabita nábojem s délkovou hustotou λ. Určete intenzitu elektrického pole:
a) ve výšce z v libovolném místě nad úsečkou,
b) ve výšce z nad středem úsečky,
c) ve výšce z nad přímkou (nekonečně dlouhou úsečkou).
Pozn.: Body b) a c) jsou speciální případy bodu a).
a) Nápověda: Obrázek a poznámka
Nejprve zvolíme soustavu souřadnou a nakreslíme si obrázek.
Pozn.: V celé úloze předpokládáme, že je úsečka (přímka) nabita kladným nábojem. Pro záporný náboj by měl vektor intenzity pouze opačný směr.
a) Nápověda: Souvislost s bodovým nábojem
Kladný bodový náboj Q vytváří ve vzdálenosti r pole o intenzitě
\[E\,=\,\frac{1}{4 \pi \varepsilon_0}\, \frac{Q}{r^2}\,.\]Vektor intenzity míří od náboje.
Zamyslete se nad tím, jak bychom tohoto poznatku mohli využít v této úloze.
a) Rozbor
Nejprve zvolíme soustavu souřadnic. Úsečka bude ležet na ose x a bod A na ose z ve vzdálenosti z od počátku. V tomto případě bude vektor intenzity ležet v rovině xz.
Úsečku rozdělíme na malé části, které se budou chovat jako bodové náboje. Celkovou intenzitu pak získáme zintegrováním příspěvků intenzit od jednotlivých kousků.
a) Řešení
Nejdříve zvolíme soustavu souřadnic.
Úsečka bude ležet na ose x a bod A bude ležet na ose z ve vzdálenosti z od počátku. Koncové body úsečky označíme a a b, což budou zároveň i x-ové souřadnice koncových bodů úsečky.

Poznámka: Pokud je úsečka umístěna tak, jak je uvedeno na obrázku, je souřadnice jejího levého krajního bodu záporná, tj. hodnota a je záporná.
Víme, že bodový náboj o velikosti Q vytváří ve vzdálenosti r elektrické pole o intenzitě:
\[ E\,=\, \frac{1}{4 \pi \varepsilon_0}\,\frac{Q}{r^2}\,.\]Úsečku si tedy rozdělíme na malé části délky dx, které budou nabity nábojem dQ = λdx a které se budou chovat jako bodový náboj.
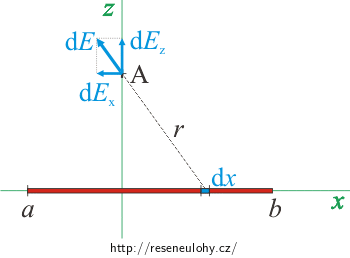
Jeden takový kousek úsečky bude tedy v bodě A (který je ve vzdálenosti r) vytvářet elektrické pole s intenzitou o velikosti:
\[ \mathrm{d}E\,=\, \frac{1}{4 \pi \varepsilon_0}\,\frac{\mathrm{d}Q}{r^2}\,=\, \frac{1}{4 \pi \varepsilon_0}\,\frac{\lambda\mathrm{d}x}{r^2}\,.\tag{*}\]Vektor intenzity pro jednotlivé příspěvky mění svůj směr. Velikost vektoru budeme tedy počítat ve složkách. Složka intenzity ve směru osy y (tj. kolmo k obrázku) je pro všechny příspěvky rovna nule. Ostatní složky vektoru vyjádříme pomocí žlutého trojúhelníku na následujícím obrázku. Nesmíme zapomenout, že složka ve směru osy x je záporná:
\[ \mathrm{d}E_\mathrm{x}\,=\,-\, \cos\alpha\,\mathrm{d}E\] \[ \mathrm{d}E_\mathrm{z}\,=\, \sin\alpha\,\mathrm{d}E\]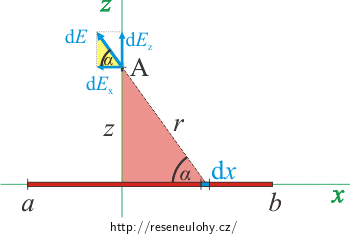
Sinus a kosinus vyjádříme pomocí stran červeného trojúhelníku:
\[\cos\alpha\,=\, \frac{x}{r},\] \[\sin\alpha\,=\, \frac{z}{r}\]a dosadíme do předchozích vzorců:
\[ \mathrm{d}E_\mathrm{x}\,=\, -\frac{x}{r}\,\mathrm{d}E,\] \[ \mathrm{d}E_\mathrm{z}\,=\,\frac{z}{r}\, \mathrm{d}E.\]Nyní dosadíme za dE ze vzorce (*):
\[ \mathrm{d}E_\mathrm{x}\,=\,- \,\frac{1}{4 \pi \epsilon_0}\,\frac{\lambda}{r^2}\,\frac{x}{r} \mathrm{d}x\,=\,- \,\frac{1}{4 \pi \epsilon_0}\,\frac{\lambda x}{r^ 3}\mathrm{d}x,\] \[ \mathrm{d}E_\mathrm{z}\,=\, \frac{1}{4 \pi \epsilon_0}\,\frac{\lambda}{r^2}\,\frac{z}{r}\mathrm{d}x\,=\, \frac{1}{4 \pi \epsilon_0}\,\frac{\lambda z}{r^3}\mathrm{d}x.\]Pomocí červeného trojúhelníka vyjádříme vzdálenost r:
\[r\,=\, \sqrt{x^2+z^2}\]a dosadíme do vyjádření obou složek:
\[ \mathrm{d}E_\mathrm{x}\,=\,- \,\frac{1}{4 \pi \epsilon_0}\,\frac{\lambda x}{\left(x^2+z^2\right)^{\frac{3}{2}} }\mathrm{d}x,\] \[ \mathrm{d}E_\mathrm{z}\,=\, \frac{1}{4 \pi \epsilon_0}\,\frac{\lambda z}{\left(x^2+z^2\right)^{\frac{3}{2}} }\mathrm{d}x.\tag{**}\]Složky vektoru celkové intenzity E získáme integrací jednotlivých příspěvků přes celou délku úsečky:
\[ E_\mathrm{x}\,=\,\int_\mathrm{a}^\mathrm{b}\mathrm{d}E_\mathrm{x},\] \[ E_\mathrm{z}\,=\,\int_\mathrm{a}^\mathrm{b}\mathrm{d}E_\mathrm{z}.\]
Za jednotlivé příspěvky dosadíme ze vzorce (**) a zintegrujeme:
\[ E_\mathrm{x}\,=\,- \,\int_\mathrm{a}^\mathrm{b}\frac{1}{4 \pi \epsilon_0}\,\frac{\lambda x}{\left(x^2+z^2\right)^{\frac{3}{2}} }\mathrm{d}x \,=\,- \,\frac{\lambda}{4 \pi \epsilon_0}\int_\mathrm{a}^\mathrm{b}\,\frac{x}{\left(x^2+z^2\right)^{\frac{3}{2}} }\mathrm{d}x,\] \[ E_\mathrm{z}\,=\,\int_\mathrm{a}^\mathrm{b}\frac{1}{4 \pi \epsilon_0}\,\frac{\lambda z}{\left(x^2+z^2\right)^{\frac{3}{2}} }\mathrm{d}x\,=\,\frac{\lambda z}{4 \pi \epsilon_0}\int_\mathrm{a}^\mathrm{b}\,\frac{1}{\left(x^2+z^2\right)^{\frac{3}{2}} }\mathrm{d}x.\]Podrobnější postup výpočtu integrálů je uveden v samostatném oddílu na konci úlohy:
\[ E_\mathrm{x}\,=\,- \,\frac{\lambda}{4 \pi \epsilon_0}\left[-\frac{1}{\sqrt{x^2+z^2} }\right]_\mathrm{a}^\mathrm{b}\,=\, \,\frac{\lambda}{4 \pi \epsilon_0}\left[\frac{1}{\sqrt{x^2+z^2} }\right]_\mathrm{a}^\mathrm{b}\] \[ E_\mathrm{z}\,=\,\frac{\lambda z}{4 \pi \epsilon_0}\left[\frac{x}{z^2\sqrt{x^2+z^2} }\right]_\mathrm{a}^\mathrm{b}\,=\,\frac{\lambda z}{4 \pi \epsilon_0 z^2}\left[\frac{x}{\sqrt{x^2+z^2} }\right]_\mathrm{a}^\mathrm{b}\] \[ E_\mathrm{z}\,=\,\frac{\lambda}{4 \pi \epsilon_0 z}\left[\frac{x}{\sqrt{x^2+z^2} }\right]_\mathrm{a}^\mathrm{b}.\]Dosadíme koncové body úsečky a máme obecné vyjádření složek elektrické intenzity:
\[ E_\mathrm{x}\,=\,\frac{\lambda}{4 \pi \epsilon_0}\,\left(\frac{1}{\sqrt{a^2+z^2} }\,-\,\frac{1}{\sqrt{b^2+z^2}}\right),\] \[E_\mathrm{y}\,=\,0,\] \[ E_\mathrm{z}\,=\,\frac{\lambda}{4 \pi \epsilon_0 z}\left(\frac{b}{\sqrt{b^2+z^2} }\,-\,\frac{a}{\sqrt{a^2+z^2} }\right).\]Nápověda k části b) a c)
Při výpočtu intenzity nad středem úsečky a přímky využijte výsledků získaných v části a), do kterých stačí dosadit krajní body a a b.
Jestliže bod A leží nad středem úsečky, můžeme krajní body a, b úsečky vyjádřit pomocí její délky \(\hspace{20px}a\,=\,-\,\frac{l}{2} \hspace{20px}\)a \(\hspace{20px} b\,=\,\frac{l}{2}\,.\)
Přímka je vlastně úsečka, která má své krajní body v nekonečnu a je tedy „nekonečně“ dlouhá, tj. \(a \to -\infty\), \(b \to \infty\,,\) resp. \(l \to \infty\) .
Rozbor k části b) a c)
Při výpočtu intenzity nad středem úsečky se výpočet zjednoduší. Úsečka je v tomto případě souměrná podle počátku. Ke každému kousku úsečky existuje jiný kousek úsečky, který je souměrný podle osy z. Vektory intenzit od těchto částí úsečky jsou také souměrné podle osy z (viz obrázek). V takovém případě jsou x-ové složky těchto vektorů stejně velké, mají opačný směr, a proto se odečtou. Celková intenzita v bodě A má tedy x-ovou i y-ovou složku rovnu nule, to znamená, že míří ve směru osy z. Její velikost získáme dosazením do výsledku předchozího výpočtu.
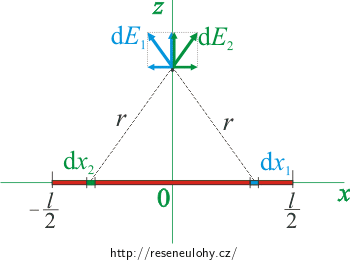
Přímka je vlastně úsečka, která má koncové body v nekonečnu. Protože přímka je také souměrná podle osy z, bude opět vektor intenzity mířit ve směru osy z stejně jako v předchozím případě. Velikost intenzity určíme tak, že délku úsečky limitně zvětšíme k nekonečnu.
b) Řešení
Při vyjadřování intenzity nad středem úsečky využijeme výsledků z části a):
\[ E_\mathrm{x}\,=\,\frac{\lambda}{4 \pi \epsilon_0}\,\left(\frac{1}{\sqrt{b^2+z^2}}\,-\,\frac{1}{\sqrt{a^2+z^2} }\right),\] \[E_\mathrm{y}\,=\,0\] \[ E_\mathrm{z}\,=\,\frac{\lambda}{4 \pi \epsilon_0 z}\,\left(\frac{b}{\sqrt{b^2+z^2} }\,-\,\frac{a}{\sqrt{a^2+z^2} }\right).\]Koncové body úsečky můžeme vyjádřit pomocí délky úsečky:
\[a\,=\,-\frac{l}{2},\] \[b\,=\,\frac{l}{2}.\]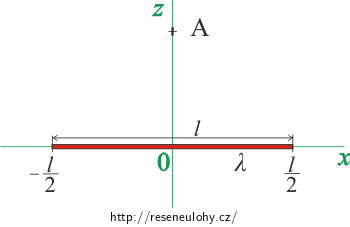
Nejdříve dopočítáme x-ovou složku intenzity:
\[ E_\mathrm{x}\,=\,\frac{\lambda}{4 \pi \epsilon_0}\,\left(\frac{1}{\sqrt{\frac{l^2}{4}+z^2} }\,-\,\frac{1}{\sqrt{\frac{l^2}{4}+z^2}}\right)\,=\,0.\]Složka je rovna nule, což jsme v Rozboru odvodili úvahou.

Nyní dopočítáme z-ovou složku intenzity, která nám zároveň udává celkovou velikost vektoru intenzity, protože obě ostatní složky jsou rovny nule.
\[ E_\mathrm{z}\,=\,\frac{\lambda}{4 \pi \epsilon_0 z}\left( \frac{\frac{l}{2}}{\sqrt{\frac{l^2}{2^2}+z^2} }\,-\,\frac{-\frac{l}{2}}{\sqrt{\frac{l^2}{2^2}+z^2} }\right).\]Výrazy v závorce sečteme a zbavíme se zlomku pod odmocninou:
\[ E_\mathrm{z}\,=\,\frac{\lambda}{4 \pi \epsilon_0 z} \,\frac{l}{\sqrt{\frac{l^2}{4}+z^2} }\,=\,\frac{\lambda}{4 \pi \epsilon_0 z} \,\frac{l}{\sqrt{\frac{l^2+4z^2}{4}} }\,=\,\frac{\lambda}{4 \pi \epsilon_0 z} \,\frac{l}{\frac{\sqrt{l^2+4z^2}}{2} },\] \[ E_\mathrm{z}\,=\,\frac{\lambda}{2 \pi \epsilon_0 z} \,\frac{l}{\sqrt{l^2+4z^2} }\]Získali jsme tedy velikost celkové intenzity elektrického pole nad středem nabité úsečky:
\[ E_\mathrm{x}\,=\,0,\] \[ E_\mathrm{y}\,=\,0,\] \[ E_\mathrm{z}\,=\,\frac{\lambda}{2 \pi \epsilon_0 z} \,\frac{l}{\sqrt{l^2+4z^2} }.\]Vektor intenzity míří ve směru osy z a má velikost
\[ E\,=\,\frac{\lambda}{2 \pi \epsilon_0 z} \,\frac{l}{\sqrt{l^2+4z^2} }\,.\]c) Řešení
Při vyjadřování intenzity nad nekonečnou přímkou využijeme výsledek z části b). Odtud víme, že vektor elektrické intenzity nad středem nabité úsečky o délce l míří ve směru z a jeho velikost je
\[ E\,=\,\frac{\lambda}{2 \pi \epsilon_0 z} \,\frac{l}{\sqrt{l^2+4z^2} }\,.\]Protože přímka je vlastně „nekonečně“ dlouhá úsečka, je třeba spočítat hodnotu intenzity E pro l jdoucí k nekonečnu:
\[ E\,=\, \lim_{\small l \tiny \to \infty } \,\frac{\lambda}{2 \pi \epsilon_0 z} \,\frac{l}{\sqrt{l^2+4z^2} }\,=\,\frac{\lambda}{2 \pi \epsilon_0 z} \, \lim_{\small l \tiny \to \infty } \,\frac{l}{\sqrt{l^2+4z^2} }.\]Délka l je mnohem větší než vzdálenost z, tj. l >> z. Člen z2 ve jmenovateli zlomku můžeme tedy vůči l2 zanedbat:
\[\lim_{\small l \tiny \to \infty } \,\large\frac{l}{\sqrt{l^2+4z^2}}\,=\,\lim_{ \small l \tiny \to -\infty }\large \,\frac{l}{\sqrt{l^2}}.\]Odmocníme jmenovatele zlomku:
\[\lim_{ \small l \tiny \to \infty }\, \large \frac{l}{\sqrt{l^2}}\,=\,\lim_{ \small l \tiny \to \infty } \large\,\frac{l}{|l|}\,=\,\lim_{ \small l \tiny \to \infty}\large\, \frac{l}{l}\,=\,\lim_{ \small l \tiny \to \infty }\large \, 1\,=\,1.\]Výsledek limity dosadíme do vztahu pro velikost intenzity E a dostáváme, že nabitá přímka vytváří ve vzdálenosti z pole o intenzitě:
\[ E\,=\,\frac{\lambda}{2 \pi \epsilon_0}\,\frac{1}{ z}\,.\]Pozn.: Intenzitu jsme mohli vypočítat také z výsledku části a). Postup je velice podobný, ale zdlouhavější.
Odpověď
a) Jestliže úsečka leží na ose x mezi body o souřadnicích [a; 0; 0] a [b; 0; 0] a bod A, ve kterém intenzitu zjišťujeme, má souřadnici [0; 0; z], pak má vektor intenzity E složky:
\[ E_\mathrm{x}\,=\,\frac{\lambda}{4 \pi \epsilon_0}\,\left(\frac{1}{\sqrt{b^2+z^2} }\,-\,\frac{1}{\sqrt{a^2+z^2} }\right)\] \[E_\mathrm{y}\,=\,0\] \[ E_\mathrm{z}\,=\,\frac{\lambda}{4 \pi \epsilon_0 z}\,\left(\frac{b}{\sqrt{b^2+z^2} }\,-\,\frac{a}{\sqrt{a^2+z^2} }\right)\]b) Ve vzdálenosti z nad středem úsečky míří vektor intenzity kolmo od úsečky a má velikost
\[ E\,=\,\frac{\lambda}{2 \pi \epsilon_0 z} \,\frac{l}{\sqrt{l^2+4z^2} }\,.\]c) Nabitá přímka vytváří ve vzdálenosti z pole o intenzitě:
\[ E\,=\,\frac{\lambda}{2 \pi \epsilon_0}\,\frac{1}{ z}\,.\]Vektor intenzity míří kolmo od přímky.
Podrobný výpočet integrálů z části a)
V následujícím oddílu vypočítáme integrály z oddílu a) Řešení.
První integrál – výpočet složky Ex:
\[E_\mathrm{x}\,=\,-\,\frac{1}{4 \pi \varepsilon_0} \int_\mathrm{a}^\mathrm{b} \frac{x}{\left( x^2\,+\,z^2\right)^{\frac{3}{2}}}\,\mathrm{d}x.\]Integrál nejprve spočteme jako neurčitý (tj. bez mezí). Integrál budeme počítat pomocí substituce:
\[t\,=\,x^2\,+\,z^2\] \[\mathrm{d}t\,=\,2x\,\mathrm{d}x \hspace{20px} \Rightarrow \hspace{20px} x\,\mathrm{d}x\,=\,\frac{\mathrm{d}t}{2}.\]Dosadíme do integrálu:
\[ \int \frac{x}{\left( x^2\,+\,z^2\right)^{\frac{3}{2}}}\,\mathrm{d}x\,=\,\int \frac{\mathrm{d}t}{2t^{\frac{3}{2}}} \,=\,\frac{1}{2}\int t^{-\frac{3}{2}}\,\mathrm{d}t\,=\,-\,\frac{1}{2} \,\frac{t^{-\frac{1}{2}}}{\frac{1}{2}}. \]Zkrátíme 1/2 a dosadíme za t:
\[ \int \frac{x}{\left( x^2\,+\,z^2\right)^{\frac{3}{2}}}\,\mathrm{d}x\,=\, - \frac{1}{\sqrt{t}},\] \[\int \frac{x}{\left( x^2\,+\,z^2\right)^{\frac{3}{2}}}\,\mathrm{d}x\,=\, - \frac{1}{\sqrt{x^2\,+\,z^2}}. \]Dosazením mezí získáme výsledek:
\[E_\mathrm{x}\,=\,-\,\frac{1}{4 \pi \varepsilon_0} \left[ - \frac{1}{\sqrt{x^2\,+\,z^2}} \right]_\mathrm{a}^\mathrm{b}\]Druhý integrál – výpočet složky Ez:
Druhý integrál
\[ E_\mathrm{z}\,=\,\frac{\lambda z}{4 \pi \epsilon_0}\int_\mathrm{a}^\mathrm{b}\,\frac{1}{\left(x^2+z^2\right)^{\frac{3}{2}} }\mathrm{d}x\]vypočítáme opět nejprve jako neurčitý a využijeme substituce, ale tentokrát je výpočet složitější. Vhodnou substitucí pro tento typ integrálu je
\[x\,=\,z \,\sinh \,t\] \[\mathrm{d}x\,=\,z\,\cosh\, t \,\mathrm{d}t.\]Dosadíme do integrálu a integrál před výpočtem ještě upravíme:
\[ \int\,\frac{1}{\left(x^2+z^2\right)^{\frac{3}{2}} }\mathrm{d}x\,=\, \int\frac{z\,\cosh \,t \,\mathrm{d}t}{\left(z^2\,\sinh^2t+z^2\right)^{\frac{3}{2}}} \,=\, \int\frac{z\,\cosh \, t \,\mathrm{d}t}{\left(z^2\right)^{\frac{3}{2}} \left(\sinh^2t+1\right)^{\frac{3}{2}}} \,=\,\]zkrátíme z a také využijeme vztah cosh2t = sinh2t + 1:
\[ \,=\, \int\frac{z\,\cosh t \,\mathrm{d}t}{z^3 \left(\cosh^2t\right)^{\frac{3}{2}} }\,=\, \int\frac{\cosh t \,\mathrm{d}t}{z^2 \,\cosh^3t }\,=\]výraz zkrátíme, vyjmeme konstanty před integrál, integrál vypočítáme a upravíme:
\[ =\, \frac{1}{z^2}\int\frac{\mathrm{d}t}{ \,\cosh^2 t }\,=\, \frac{1}{z^2} \,\tanh\, t\,=\, \frac{1}{z^2}\, \frac{\sinh\, t}{\cosh\, t} \,=\, \frac{1}{z^2}\frac{\sinh \,t}{\sqrt{1+\sinh^2 t}} \,=\]dosadíme zpět x ze substituce a upravíme složený zlomek:
\[ \,=\, \frac{1}{z^2} \frac{\frac{x}{z}}{\sqrt{1+\frac{x^2}{z^2}}} \,=\, \frac{1}{z^2} \frac{x}{z \sqrt{\frac{x^2+z^2}{z^2}}} \,=\, \frac{1}{z^2}\, \frac{x}{ \sqrt{x^2+z^2}}. \]Nyní už jen dosadíme meze:
\[ E_\mathrm{z}\,=\, \frac{\lambda z}{4 \pi \epsilon_0}\frac{1}{z^2}\, \left[ \frac{x}{ \sqrt{x^2+z^2}} \right]_\mathrm{a}^\mathrm{b} \,=\, \frac{\lambda}{4 \pi \epsilon_0\,z}\,\left[ \frac{x}{ \sqrt{x^2+z^2}} \right]_\mathrm{a}^\mathrm{b}.\]Odkaz: Jak jinak vypočítat intenzitu v okolí přímky?
Intenzity elektrického pole v okolí přímky můžeme vypočítat také pomocí Gaussovy věty. Tento postup je uveden v úloze Pole nabité přímky.




