Druh pohybu, tvar trajektorie
Úloha číslo: 191
Pohyb tělesa je dán rovnicemi
\(x\, =\, A \cos(\omega t)\,,\)
\( y\, = \,B \cos(2 \omega t)\,,\)
kde A, B jsou konstanty.
Určete rovnici trajektorie a nakreslete ji pro A = B = 1.
Nápověda 1: Trajektorie pohybu
Jak lze určit závislost y = y(x) (křivka popisující trajektorii pohybu) z parametrického vyjádření zadané křivky?
Nápověda 2: Křivka
Jakou geometrickou křivku popisuje vámi spočítaná rovnice?
Řešení
Pokud chceme získat závislost y = y(x), musíme z parametrického vyjádření vyloučit parametr t.
Z rovnice pro x vyjádříme cos(ωt):
\[x \,=\, A \cos(\omega t )\,\, \Rightarrow \,\,cos(\omega t) \,=\, \frac{x}{A}.\]Nyní rovnici pro y upravíme tak, abychom do ní mohli dosadit za cos(ωt):
\[y \,= \,B \cos(2\omega t)\, =\, B \cos^{2} (\omega t) \,- \,B \sin^{2} ( \omega t)\, = \, B \cos^{2} (\omega t) \,- \] \[- \,B\left[ 1\, - \, \cos^{2} ( \omega t)\right] \, = \, 2B \cos^{2} (\omega t)\, - \,B,\] \[y \,=\,2B \cos^{2} (\omega t)\, - \,B\]Do takto upravené rovnice dosadíme za cos(ωt) výraz z první rovnice, tím získáme hledanou závislost:
\[y \, =\, 2B\left(\frac{x}{A}\right)^{2} \, -\, B \, =\,\frac{2B}{A^{2}}x^{2}\, - \,B\,.\]Touto rovnicí je dána parabola s vrcholem v bodě [0; −B]. Pro A = B = 1 dostáváme předpis
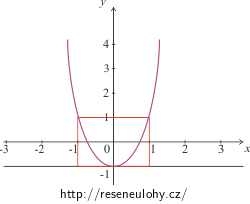
\[y \,=\, 2x^{2}\, - \,1\,,\]jehož graf je znázorněn na obrázku.
Vraťme se k parametrickým rovnicím v zadání popisujícím daný pohyb. Funkce cosinus nabývá hodnot od -1 do 1. Trajektorií pohybu bude tedy jen část paraboly daná obdélníkem o stranách od -A do A a od -B do B. Pro naše zadané hodnoty je obdélník vyznačen v obrázku.
Odpověď
Poznámka
Podívejme se ještě, o jaký pohyb se jedná. Rovnice popisují harmonický kmitavý pohyb. Jde tedy o skládání dvou kolmých kmitů. Výslednou trajektorií je jeden z tvarů Lissajousovy křivky.