Sbírka řešených úloh

Délka oblouku cykloidy

Úloha číslo: 2037

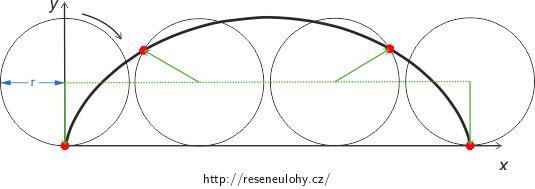
Cykloida je křivka, jejíž tvar opíše libovolný bod kružnice, která se bez prokluzu valí po přímce. Řekněme, že ve svém nejvyšším bodě má výšku 2r, kde r je poloměr valící se kružnice.

Určete délku jednoho jejího oblouku.

• Nápověda

  Tato úloha přímo navazuje na úlohu Parametrické vyjádření cykloidy, kde je vysvětlen postup pro odvození parametrických rovnic cykloidy nezbytných pro vyřešení této úlohy.

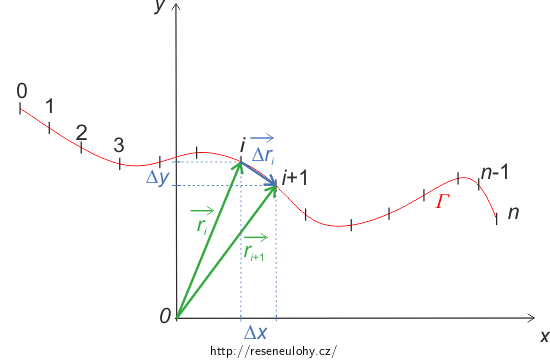
  Pokud přímo neznáte vyjádření délky obecné křivky v prostoru, pokuste se jej odvodit. Libovolnou jednoduchou křivku si nakreslete a přemýšlejte, jak spočítat délku nějaké její malé části.

  Vzhedem k tomu, že většina křivek, včetně naší cykloidy, bývá vyjádřena parametricky, pokuste se do výpočtu zakomponovat parametr t.

  Jakou matematickou operaci znáte, která by dokázala sečíst všechny malé úseky křivky?

• Řešení nápovědy

  Začneme tedy nakreslením si libovolné křivky Γ do kartézského souřadnicového systému (křivka je na obrázku níže červeně).

  

  Předpokládáme, že známe parametrické vyjádření této křivky, ale neumíme spočíst její délku nijak přímo. Proto si nejprve zkusíme vyjádřit délku jednoho malého kousku. Pro tento účel si křivku rozdělíme na množství dílků, které budou tak malé, že je bude možné považovat za rovné (v obrázku jsou pro přehlednost větší). Dělící body si označíme 0, 1, 2, 3,…, n−1, n.

  Zkusme vyjádřit délku některého náhodného dílku. Zvolíme si obecný — mezi body i a i+1. K vyjádření vzdálenosti použijeme rozdíl jejich vektorů. Vektory si označíme podle dělícího bodu, kterému přísluší a zakreslíme do obrázku. Rozdíl označíme symbolem Δ a vyjádříme si jej souřadnicově.

  \[\Delta \vec r_i=\vec r_{i+1}-\vec r_{i}=(x_{i+1}-x_i \space ;\space y_{i+1}-y_i)=(\Delta x;\Delta y)\]

  Ze souřadnicového tvaru vektoru dokážeme lehce spočítat jeho velikost pomocí Pythagorovy věty.

  \[|\Delta \vec r_i|= \sqrt{(\Delta x)^2+(\Delta y)^2}\]

  Naše křivka je zadaná parametricky — s proměnným parametrem t. Na tomto parametru jsou závislé i průměty elementů křivky do souřadných os, neboli složky. Nás tím pádem bude nejvíce zajímat, jak se bude průběh křivky měnit s měnícím se t. Měnící se t vyjádříme pomocí Δt a abychom nezměnili nijak hodnotu výrazu, musíme jím rovnici vynásobit i vydělit.

  \[ |\Delta \vec r_i|= \sqrt{(\Delta x)^2+(\Delta y)^2}\cdot \frac{\Delta t}{\Delta t}=\sqrt{\left( \frac{\Delta x}{\Delta t} \right)^2+ \left( \frac{\Delta y}{\Delta t} \right)^2} \Delta t\tag{1}\]

  Dále víme že vektor Δr_i je svou velikostí roven délce úsečky mezi body i a i+1. Úsečku, část křivky Γ, si označme Δs.

  \[\Delta s=|\Delta \vec r_i|\] Pokud bychom znali velikosti všech těchto malých úseček, stačilo by jednoduše je sečíst a získali bychom délku celé křivky. \[s_\Gamma = \sum_{i=0}^n \Delta s_i\]

  Nyní je zapotřebí náš výpočet zpřesnit. Toho lze dosáhnout zjemněním dělení křivky, neboli zvýšením počtu dílků. Tento proces je možné zapsat matematicky pomocí limity:

  \[s_\Gamma = \lim_{n \to \infty } \sum_{i=0}^n \Delta s_i\]

  A tento výraz je až příliš podobný definici integrálu, ihned toho tedy využijeme.

  \[s_\Gamma =\int_{a}^{b} \, \mathrm{d}s\]

  Místo rovnice (1) můžeme tedy pro délku křivky psát:

  \[s_\Gamma = \int_{a}^{b} \sqrt{\left( \frac{\mathrm{d} x}{\mathrm{d} t} \right)^2+ \left( \frac{\mathrm{d} y}{\mathrm{d} t} \right)^2} \mathrm{d} t,\]

  pro t ∈ ‹a;b›

  A to je výsledný vzorec pro výpočet délky křivky, který jsme hledali. Je samozřejmě možné tento postup zobecnit na trojrozměrný prostor přidáním z-ové složky.

• Řešení

  Pokud známe parametrické vyjádření cykloidy a vzorec pro výpočet délky křivky v prostoru, je zbytek „jen“ výpočtem derivací a integrálu.

  První krok bude spočívat v dosazení parametrických rovnic cykloidy do rovnice pro délku křivky.

  Parametrické vyjádření cykloidy je

  \[x\,=\,r\cdot(t-\sin t)\] \[y\,=\,r\cdot (1-\cos t).\]

  Ze vzorce pro výpočet délky křivky víme, že budeme potřebovat derivace všech složek cykloidy podle parametru t.

  \[\frac{\mathrm{d}x}{\mathrm{d}t}=r-r \cos t\] \[\frac{\mathrm{d}y}{\mathrm{d}t}=r\sin t\]

  Dále připravené derivace dosadíme do vzorce pro délku křivky s_Γ (viz Řešení nápovědy). Nezapomeňte že pod odmocninou jsou derivace na druhou!. Obecný vztah

  \[s_\Gamma = \int_{a}^{b} \sqrt{\left( \frac{\mathrm{d} x}{\mathrm{d} t} \right)^2+ \left( \frac{\mathrm{d} y}{\mathrm{d} t} \right)^2} \mathrm{d} t\]

  dá po dosazení

  \[s_c=\int_{a}^{b}\sqrt{(r-r\cos t)^2+(r\sin t)^2} \mathrm{d}t.\]

  Pro výpočet integrálu bude zapotřebí určit integrační meze a a b, neboli odkud kam budeme integrovat. Pro jejich určení stačí zjistit, jakých hodnot bude nabývat parametr t. Nevíme-li to ihned, stačí se zamyslet: chceme znát délku jednoho oblouku cykloidy, tzn. že hodnota y musí začít od nuly, dostat se do maxima a opět se vrátit do nuly. (Představte si jak bod, který vykresluje křivku, putuje). Podíváme-li se na parametrické vyjádření y-ové složky, vidíme že přesně to zajišťuje funkce cosinus, a ta se začne opakovat po 2π. Integrační meze tedy budou:

  \[a=0 \;,\; b=2\pi\]

  Dalším krokem bude zjednodušit výraz uvnitř integrálu.

  Využijeme vzorec pro výpočet druhé mocniny rozdílu a upravíme běžnými algebraickými pravidly.

  \[s_c=\int_{0}^{2\pi}\sqrt{r^2-2r^2\cos t+r^2\cos^2 t+r^2\sin^2 t}\space \mathrm{d}t\]

  Poloměr r je v každém členu a jedná se o konstantu, můžeme jej tedy vytknout před integrál.

  \[s_c=\int_{0}^{2\pi}r\sqrt{1-2\cos t+\cos^2 t+\sin^2 t}\space \mathrm{d}t\]

  Součet druhých mocnin sinu a cosinu je známá „goniometrická jednička”.

  \[s_c=\int_{0}^{2\pi}r\sqrt{2-2\cos t}\space \mathrm{d}t\]

  Tento výraz stále nedokážeme přímo zintegrovat. Zamyslíme se, jaké další goniometrické vztahy známe a jakého bychom mohli využít.

  Výraz pod odmocninou je nejpodobnější pravé straně vzorce

  \[|\sin{\frac{\alpha}{2}}|=\sqrt{\frac{1-\cos{\alpha}}{2}}.\]

  Abychom se k tomuto tvaru dostali, provedeme následující operace:

  \[s_c=r\int_{0}^{2\pi}\sqrt{2}\sqrt{1-\cos t}\space \mathrm{d}t \space\space /\cdot \frac{\sqrt {2}}{\sqrt{2}}\] \[s_c=r\int_{0}^{2\pi}2\sqrt{\frac{1-\cos t}{2}}\space \mathrm{d}t\] \[s_c=r\int_{0}^{2\pi}2|\sin{\frac{t}{2}}|\space \mathrm{d}t\]

  Nyní vyvstává otázka, co s absolutní hodnotou. Co zde vlastně způsobuje?

  Absolutní hodnota způsobí, že i když bude sinus záporný, výsledek v absolutní hodnotě bude kladný. Sinus bude záporný, pokud hodnota jeho argumentu bude ležet v lichém celočíselném násobku intervalu (π;2π). My ale víme, že t nabývá hodnot ‹0;2π) a celý argument sin(t/2) tím pádem ‹0;π). Na tomto intervalu nabývá sinus jen kladných hodnot, absolutní hodnotu můžeme tedy vynechat.

  \[s_c=2r\int_{0}^{2\pi}\sin{\frac{t}{2}}\space \mathrm{d}t\]

  Zbývá problém se zlomkem. Ten vyřeší vhodná substituce.

  \[u=\frac{t}{2}\] \[\mathrm{d}u=\frac{1}{2}\mathrm{d}t\] \[2\mathrm{d}u=\mathrm{d}t\]

  Bude samozřejmě zapotřebí přepočíst také integrační meze dosazením do první substituční rovnice.

  \[u_a=\frac{t_a}{2}=\frac{0}{2}=0\] \[u_b=\frac{t_b}{2}=\frac{2\pi}{2}=\pi\]

  Integrál bude mít po substituci tvar

  \[s_c=2r\int_{0}^{\pi}2\sin{u}\space \mathrm{d}u.\]

  Takový integrál již dovedeme snadno spočítat.

  \[s_c=4r[-\cos u]_0^\pi=4r(-\cos\pi-(-\cos 0))=4r[-(-1)-(-1)]\]

  Výsledná délka jednoho oblouku cykloidy je tedy

  \[s_c=8r.\]

• Odpověď

  Délka jednoho oblouku cykloidy:

  \[s_c=8r\]

• Podobná úloha

  Pokud potřebujete procvičovat dále, nebo problematiku lépe pochopit, podívejte se na podobnou úlohu Jedoucí kolo.