Těžiště čtvrtkruhu
Úloha číslo: 1119
Určete polohu těžiště homogenního čtvrtkruhu o poloměru R.
Nápověda 1
Zamyslete se nad tím, co vlastně znamená úkol „určete polohu těžiště“. Co má být výstupem úlohy, co vlastně určujete?Nápověda 2
Vhodným způsobem umístěte čtvrtkruh do souřadného systému. Lze jej tam umístit tak, aby se další výpočty zjednodušily? Jak takové zjednodušení vypadá?
Nápověda 3
Jak je obecně definován vztah pro výpočet polohového vektoru rT, který určuje polohu těžiště?Nápověda 4
Čtvrtkruh v zadání úlohy výše je homogenní. Využijte toho k tomu, abyste od hmotnostních elementů ve vztahu (1) přešli k elementům plošným.
Nápověda 5
Jak se změní vztah (2), pokud se budeme (dle počáteční úvahy) zabývat pouze y-ovou souřadnicí těžiště yT?
Nápověda 6
Nyní je nutné vhodně rozepsat integrační element dS do kartézských souřadnic. Jednou z možností je rozdělit čtvrtkruh na vodorovné proužky. Ty můžeme při dostatečně jemném dělení považovat za obdélníčky o výšce dy, které mají proměnnou šířku (označme ji např. r). Nakreslete si obrázek popisující úvahu výše a pokuste se podle něj upravit integrál ze vztahu (3) tak, aby v něm figurovaly pouze integrační element dy, proměnná y a konstanty.Nápověda 7
Nyní již doplňte ve vztahu (6) pouze integrační meze a integrál dopočítejte.
Celkové řešení
Určit polohu těžiště znamená určit souřadnice těžiště v nějakém vhodně zvoleném souřadném systému. Protože čtvrtkruh je rovinný útvar (třetí rozměr, „výšku“, zanedbáváme), jsou výstupem úlohy dvě souřadnice těžiště T: xT, yT.
Čtvrtkruh umístíme do roviny xy například podle obrázku níže. Pro toto umístění jsou prováděny další výpočty.
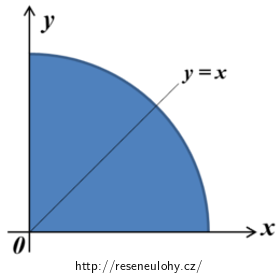
Z obrázku je patrné, že nyní stačí určit pouze y-ovou souřadnici těžiště yT. Obrazec je souměrný podle přímky y = x, jeho těžiště tedy bude ležet na této přímce a bude platit yT = xT.
Polohový vektor rT určující polohu těžiště daného objektu lze určit jako:
\[\vec{r}_\mathrm{T}\,=\,\frac{\int{\vec{r}}dm}{{\int}dm}.\tag{1}\]Element hmotnosti dm lze pro homogenní čtvrtkruh rozepsat jako součin:
\[dm\,=\,{\rho}dS,\]
kde ρ je plošná hustota materiálu a dS je plošný element. Pak platí:
\[\vec{r}_\mathrm{T}\,=\,\frac{{\rho}\int{\vec{r}}dS}{{\rho}{\int}dS}\,=\,\frac{\int{\vec{r}}dS}{{\int}dS}.\]Výraz ve jmenovateli představuje vysčítání všech plošných elementů, kterými je čtvrtkruh tvořen – dostáváme zde tedy obsah plochy celého čtvrtkruhu S:
\[\vec{r}_\mathrm{T}\,=\,\frac{\int{\vec{r}}dS}{S}.\tag{2}\]Protože souřadnice polohového vektoru rT se ve vztazích (1) i (2) počítají po složkách, lze jednoduše pro námi požadovanou y-ovou souřadnici psát:
\[y_\mathrm{T}\,=\,\frac{\int{y}dS}{S}.\tag{3}\]Pro převedení dvojného integrálu ve vztahu (3) na integrál jednorozměrný si celý čtvrtkruh rozdělíme vodorovnými řezy na soustavu obdélníčků výšky dy a proměnné šířky r (viz obrázek).
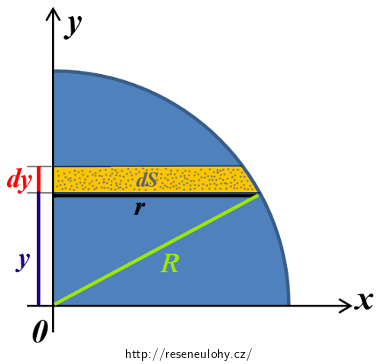
Dle obrázku výše je patrné, že plošný element dS lze pro dostatečně malé dy rozepsat jako:
\[dS\,=\,rdy.\tag{4}\]Přitom pro r můžeme z Pythagorovy věty odvodit:
\[r\,=\,\sqrt{R^2\,-\,y^2}.\tag{5}\]Dosazením rovnic (4) a (5) do vztahu (3) dostáváme:
\[y_\mathrm{T}\,=\,\frac{\int{y\sqrt{R^2\,-\,y^2}}dy}{S}.\]Doplnit můžeme ještě obsah plochy čtvrtkruhu S, který je roven S = πR2/4:
\[y_\mathrm{T}\,=\,\frac{4\int{y\sqrt{R^2\,-\,y^2}}dy}{{\pi}R^2}\,=\,\frac{4}{{\pi}R^2}\int{y\sqrt{R^2\,-\,y^2}}dy.\tag{6}\]Abychom obsáhli celý čtvrtkruh, budeme integrovat od y = 0 do y = R:
\[y_\mathrm{T}\,=\,\frac{4}{{\pi}R^2}\int_0^R{y\sqrt{R^2\,-\,y^2}}dy.\]Pro další výpočet použijeme tuto substituci:
\[R^2\,-\,y^2\,=\,t,\] \[-2ydy\,=\,dt.\]Integrál dostane následující podobu (neopomeňte změnu integračních mezí):
\[y_\mathrm{T}\,=\,\frac{4}{{\pi}R^2}{\cdot}(-\frac{1}{2})\int_{R^2}^0{t^{\frac{1}{2}}}dt\,=\,-\frac{2}{{\pi}R^2}{\cdot}\frac{2}{3}[t^{\frac{3}{2}}]_{R^2}^0\,=\,\frac{4}{3{\pi}R^2}{\cdot}(R^3)\,=\,\frac{4R}{3\pi}.\]Dle úvahy v úvodu úlohy je tedy:
\[y_\mathrm{T}\,=\,x_\mathrm{T}\,=\,\frac{4R}{3\pi}.\]Alternativní řešení
Ukážeme si ještě jiné možné řešení úlohy, spočívající v jiném matematickém přístupu. Úvodní úvahy jsou zcela stejné jako ve výše uvedeném postupu, liší se ale výpočet integrálu ve vztahu (3).
Tento dvojný integrál si přepíšeme do polárních souřadnic, jejichž střed je identický se středem našeho kartézského systému. Buď z obrázku (viz níže, pozor, malé r zde má jiný význam než na předcházejících obrázcích!), nebo ze znalosti práce s polárními souřadnicemi lze psát:
\[\sin{\varphi}\,=\,\frac{y}{r}\,\Rightarrow\,y\,=\,r\sin\varphi,\tag{7}\] \[dS\,=\,rdrd\varphi.\tag{8}\]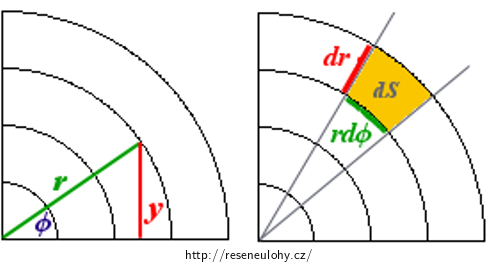
Vztahy (7) a (8) dosadíme do rovnice (3), stejně jako obsah čtvrtkruhu S:
\[y_\mathrm{T}\,=\,\frac{\int\int{r\sin{\varphi}rdrd\varphi}}{\frac{{\pi}R^2}{4}}\,=\,\frac{4}{{\pi}R^2}\int\int{r^2\sin{\varphi}drd\varphi}.\]Nyní určíme integrační meze: Abychom pokryli celý čtvrtkruh, budeme integrovat v proměnné r od r = 0 do r = R a v proměnné φ od φ = 0 do φ = π/2:
\[y_\mathrm{T}\,=\,\frac{4}{{\pi}R^2}\int_0^R\int_0^{\frac{\pi}{2}}{r^2\sin{\varphi}drd\varphi}\,=\,\frac{4}{{\pi}R^2}\int_0^R{r^2dr}\int_0^{\frac{\pi}{2}}{\sin{\varphi}d\varphi},\] \[y_\mathrm{T}\,=\,\frac{4}{{\pi}R^2}{\cdot}\frac{1}{3}[r^3]_0^R{\cdot}[-\cos{\varphi}]_0^{\frac{\pi}{2}}\,=\,\frac{4}{{\pi}R^2}{\cdot}\frac{1}{3}R^3{\cdot}1\,=\,\frac{4R}{3\pi}.\]I tímto postupem tedy dostáváme:
\[x_\mathrm{T}\,=\,y_\mathrm{T}\,=\,\frac{4R}{3\pi}.\]Odpověď
Pro souřadnice těžiště v námi zvoleném souřadném systému platí:
\[x_\mathrm{T}\,=\,\frac{4R}{3\pi},\] \[y_\mathrm{T}\,=\,\frac{4R}{3\pi}.\]



