Obsah kruhu
Úloha číslo: 999
a) Odvoďte známý vztah pro obsah kruhu o poloměru R pomocí jednorozměrného integrálu a substituční metody.
b) Nezávisle na výsledku úlohy a) vypočítejte obsah kruhu s jednotkovým poloměrem, kdy k výpočtu použijete jednorozměrný integrál a metodu per partes.
Nápověda 1 ( k úloze a) )
Úlohou je odvodit vztah pro obsah kruhu o poloměru R pomocí jednorozměrného integrálu a substituční metody.
Nakreslete si nejdřív kartézskou soustavu souřadnic a rozmyslete si, kam by bylo nejvýhodnější kruh umístit, abyste mohli využít symetrii.
Díky symetrii postačí vypočítat obsah jedné poloviny kruhu, například „horní“ (výsledný obsah pak bude dvojnásobný). Zamyslete se, která funkce má za graf „horní“ půlkružnici.
Sestavte určitý integrál a zamyslete se, jaké budou jeho meze.
Rozmyslete si, jakou substituci bude nejvýhodnější použít.
Nápověda 2 ( k úloze b) )
Úlohou je vypočítat obsah kruhu s jednotkovým poloměrem, kdy se k výpočtu použije jednorozměrný integrál a metoda per partes.
Postup je analogický jako v úloze a). Nakreslete si soustavu souřadnic, vhodně do ní umístěte kruh a při výpočtu využijte symetrii.
Sestavte určitý integrál a vyřešte ho metodou per partes.
Celkové řešení
ad a)
Střed kruhu umístíme do počátku soustavy souřadnic, jak je možné vidět na obrázku níže.
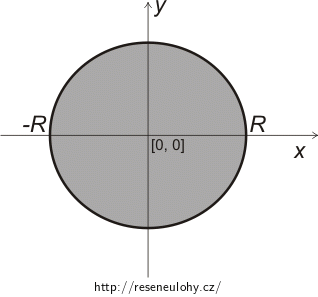
Využijeme symetrii a spočítáme obsah „horní“ poloviny kruhu. Víme, že všechny body hraniční kružnice splňují rovnici
\[ x^2 + y^2 = R^2. \]Funkci, která má za graf „horní“ půlkružnici, dostaneme vyjádřením y z předešlé rovnice. Pro „horní“ polovinu vezmeme jenom \[y \ge 0\]
\[ y = \sqrt{R^2 - x^2} . \]Vyjádřili jsme y jako funkci x, proto budeme integrovat přes všechna x od -R do R (viz obrázek nahoře).
Pro polovinu obsahu podle definice určitého integrálu (jako „obsahu plochy pod grafem funkce“) platí:
\[ \frac{1}{2} S = \int_{-R}^{R}\sqrt{R^2 - x^2} \mathrm{d}x. \]Nyní využijeme substituci:
\[ x = R\sin t \hspace{20px} \Rightarrow \hspace{20px} \mathrm{d}x = R\cos t \mathrm{d}t . \]Vypočteme, jak se změní meze:
pro x = -R dostáváme \[t = -\frac{\mathrm{\pi}}{2},\]
pro x = R dostáváme \[t = \frac{\pi}{2}.\]
Pro poloviční obsah platí
\[ \frac{1}{2}S = \int_{-\frac{\mathrm{\pi}}{2}}^{\frac{\pi}{2}}\sqrt{R^2 - R^2\sin^2 t} \underbrace{R \cos t \mathrm{d}t}_{\mathrm{d}x}= \] \[ = \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\sqrt{R^2(1 - \sin^2 t)} R \cos t \mathrm{d}t = \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\sqrt{R^2 \cos^2t} R \cos t \mathrm{d}t = \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}R^2 |\cos t|\cos t \mathrm{d}t, \]kde jsme využili vztah \[\cos^2t + \sin^2t = 1.\]
Absolutní hodnotu lze vynechat, protože funkce kosinus nabývá v intervalu \[(-\frac{\pi}{2}, \hspace{2px}\frac{\pi}{2})\] jenom kladných hodnot.
Dostáváme
\[ \frac{1}{2}S= \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}R^2 \cos^2 t \mathrm{d}t .\]Využijeme známý vzorec \[cos^2t = \frac{1 + \cos 2t}{2}\]
\[ \frac{1}{2}S = \frac{1}{2} R^2\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}(1 + \cos 2t ) \mathrm{d}t, \] \[ S = R^2\left[t + \frac{1}{2}\sin 2t\right]_{-\frac{\pi}{2}}^{\frac{\pi}{2}} = R^2\left(\frac{\pi}{2} + \frac{1}{2}\cdot 0 -\left(-\frac{\pi}{2} + \frac{1}{2}\cdot 0\right)\right). \]Dostáváme známý vztah
\[ S = \pi R^2. \]ad b)
Na obrázku níže můžeme vidět kruh se středem v počátku kartézské soustavy souřadnic.
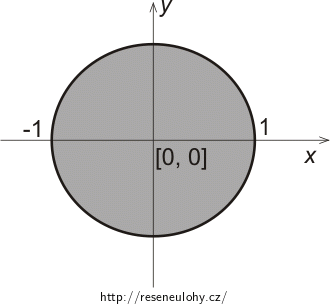
Z předešlé úlohy víme, že „horní“ hraniční kružnice je popsána rovnicí:
\[ y = \sqrt{1 - x^2}, \]kde jsme dosadili za poloměr R = 1.
Pro obsah poloviny kruhu pak platí:
\[ \frac{1}{2} S = \int_{-1}^{1}\sqrt{1 - x^2} \mathrm{d}x. \]Daný integrál nyní vyřešíme metodou per partes:
\[\frac{1}{2} S = \int_{-1}^{1}1\cdot\sqrt{1 - x^2} \mathrm{d}x = \begin{vmatrix} u^\prime= 1 & v = \sqrt{1 - x^2} \\ u = x & \hspace{3px} v^\prime= \frac{-2x}{2\sqrt{1-x^2}} \end{vmatrix} = \left[ x\sqrt{1 - x^2}\right]_{-1}^{1} - \bigg(-\int_{-1}^{1}\frac{x^2}{\sqrt{1 - x^2}}\mathrm{d}x\bigg)= \] \[ = 0 + \int_{-1}^{1}\bigg(\frac{x^2 - 1}{\sqrt{1 - x^2}} + \frac{1}{\sqrt{1 - x^2}}\bigg)\mathrm{d}x= \int_{-1}^{1}\bigg(\frac{-(1 - x^2)}{(1 - x^2)^{\frac{1}{2}}} + \frac{1}{\sqrt{1 - x^2}}\bigg)\mathrm{d}x=, \]využijeme linearitu integrálu (tj. integrál součtu je součet integrálů)
\[ = -\underbrace{\int_{-1}^{1}\sqrt{1 - x^2}\mathrm{d}x}_{\frac{1}{2}S} + \int_{-1}^{1} \frac{\mathrm{d}x}{\sqrt{1 - x^2}} = - \frac{1}{2}S + \left[\arcsin x \right]_{-1}^{1}. \]Porovnáme levou a pravou stranu rovnosti
\[ \frac{1}{2}S = - \frac{1}{2}S + \pi. \]Pro obsah kruhu s poloměrem R = 1 platí:
\[S = \pi,\]což jsme očekávali již podle řešení úlohy a).
Odpověď
a) Odvodili jsme známý vztah
\[S = \pi R^2\]pro obsah kruhu o poloměru R pomocí substituční metody.
b) Spočetli jsme (nezávisle na výsledku úlohy a) ) obsah kruhu s jednotkovým poloměrem
\[ S = \pi , \]kdy sme k výpočtu použili metodu per partes.

