Pohyb nabité částice v homogenním elektrickém a magnetickém poli
Úloha číslo: 265
Nápověda
Jestliže je částice v elektromagnetickém poli, působí na ní Lorentzova síla, která způsobí, že se částice začne pohybovat. Pro určení trajektorie sestavíme pohybovou rovnici pro pohyb částice a tu budeme řešit.
Rozbor
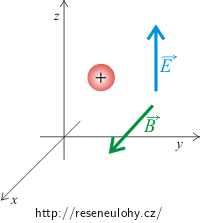
Částice se nachází v elektromagnetickém poli, které charakterizují dvě na sebe kolmé složky: elektrická, charakterizovaná elektrickou intenzitou, a magnetická, charakterizovaná magnetickou indukcí. Obě pole působí na částici silou. Elektrická složka působí na částici silou ve stejném směru, jako je směr elektrické intenzity, tedy v kladném směru osy z. Směr magnetické síly je kolmý na vektor magnetické indukce, která má v našem případě směr v kladném směru osy x. Síla bude tedy na částici působit v rovině yz. Protože je částice na počátku v klidu, bude se jednat o pohyb částice v rovině.
Sestavíme pohybovou rovnici pro pohyb nabité částice a tu budeme řešit.
Řešení
Ve směru osy x nepůsobí na částici žádná síla. Elektrická síla totiž působí ve směru elektrické intenzity, tj. stále ve směru osy z a magnetická síla je kolmá na magnetickou indukci, která má směr osy x. Výsledná síla tak bude působit v rovině yz. Protože byla částice na začátku v klidu, bude se pohybovat pouze v rovině yz. Její polohu označíme:
\[\vec{r}(t)=\left(0,\,y(t),\,z(t)\right).\]Po zderivování dostáváme okamžitou rychlost částice:
\[\vec{v}(t)=(0,\,v_\mathrm{y}(t),\,v_\mathrm{z}(t))=(0,\,\dot y(t),\,\dot z(t)).\]Lorentzova síla působící na částici v elektromagnetickém poli má tvar:
\[\vec{F}=Q\,(\vec{E}+\vec{v}\times\vec{B}).\]Sílu \(\vec{F}\) si z 2. Newtonova zákona vyjádříme jako součin hmotnosti a zrychlení:
\[\vec{F}=m\vec{a}=m \vec{\dot v}.\]Pohybová rovnice bude mít tedy tvar:
\[m\vec{\dot v}=Q(\vec{E}+\vec{v}\times\vec{B}).\]Vektory elektrické indukce a magnetické indukce si rozepíšeme do složek:
\[\vec{E}=(0,\,0,\,E)\hspace{10px} \vec{B}=(B,\,0,\,0).\]Vyjádříme vektorový součin:
\[\vec{v}\,\times\,\vec{B}=(0,\,\dot y,\,\dot z)\,\times \,(B,\,0,\,0)=(0,\,B\dot z,\,-B\dot y).\]Jednotlivé složky pohybové rovnice jsou:
\[m\dot v_\mathrm{x}=0,\] \[m\dot v_\mathrm{y}=0+QB v_\mathrm{z},\] \[m\dot v_\mathrm{z}=QE-QBv_\mathrm{y}.\]Síla ve směru osy x nepůsobí, to nám říká první pohybová rovnice. Rychlost musí být konstantní, ale tou konstantou je nula. Částice se tak podle našeho předpokladu bude pohybovat pouze v rovině yz:
\[\dot v_\mathrm{y}=\frac{QB}{m} v_\mathrm{z},\tag{1}\] \[\dot v_\mathrm{z}=\frac{QE}{m}-\frac{QB}{m}v_\mathrm{y}.\tag{2}\]Získali jsme soustavu dvou diferenciálních rovnic.
Z rovnice (1) vyjádříme rychlost vz:
\[v_\mathrm{z}= \frac{m}{QB}\dot v_\mathrm{y}\]a zderivujeme ji podle času:
\[\dot v_\mathrm{z}= \frac{m}{QB}\ddot v_\mathrm{y}.\]Tento výraz dosadíme do rovnice (2):
\[\frac{m}{QB}\ddot v_\mathrm{y}=\frac{QE}{m}-\frac{QB}{m}v_\mathrm{y}.\]Vynásobíme výrazem \[\frac{QB}{m}\] a upravíme:
\[\ddot v_\mathrm{y}+\,\left(\frac{QB}{m}\right)^2v_\mathrm{y} =\,\left(\frac{Q}{m}\,\right)^2EB.\]Tím jsme získali jednu nehomogenní lineární diferenciální rovnici s konstantními koeficienty. Podrobný postup jejího řešení je uveden v následujícím oddíle.
Řešení diferenciální rovnice
Rovnice tvaru
\[\ddot v_\mathrm{y}+\,\left(\frac{QB}{m}\right)^2v_\mathrm{y} =\,\left(\frac{Q}{m}\,\right)^2EB\tag{3}\]je nehomogenní lineární diferenciální rovnice s konstantními koeficienty. Její řešení se skládá z několika kroků.
Nejdříve vyřešíme homogenní diferenciální rovnici. Tedy rovnici, která má na pravé straně nulu. Pak budeme hledat partikulární řešení, což je libovolné řešení nehomogenní diferenciální rovnice. Tedy rovnice, která má na pravé straně konstantu. Obecné řešení nehomogenní diferenciální rovnice získáme jako součet obecného řešení homogenní rovnice a partikulárního řešení. Konstanty v obecném řešení získáme z počátečních podmínek.
a) Řešení homogenní diferenciální rovnice
\[\ddot v_\mathrm{h}+\,\left(\frac{QB}{m}\right)^2v_\mathrm{h} =0\]Řešení této rovnice hledáme ve tvaru:
\[v_\mathrm{h}(t)=e^{\alpha \mathrm{t}},\] \[\ddot v_\mathrm{h}(t)=\alpha^2e^{\alpha \mathrm{t}}.\]Po dosazení a zkrácení nenulovým výrazem \(e^{\alpha \mathrm{t}}\) dostáváme charakteristickou rovnici:
\[\alpha^2 e^{\alpha \mathrm{t}}+\,\left(\frac{QB}{m}\right)^2e^{\alpha \mathrm{t}}=0,\] \[\alpha^2+\,\left(\frac{QB}{m}\right)^2=0,\]což je kvadratická rovnice pro neznámou proměnou α. Její řešení jsou:
\[\alpha^2=-\,\left(\frac{QB}{m}\right)^2,\] \[\alpha=\pm i\,\left(\frac{QB}{m}\right).\]Pro přehlednost označme
\[\Omega=\frac{QB}{m}.\]Homogenní diferenciální rovnice má dvě nezávislá řešení:
\[v_\mathrm{h1}(t)=e^{\mathrm{i}\Omega \mathrm{t}},\] \[v_\mathrm{h2}(t)=e^{\mathrm{-i}\Omega \mathrm{t}}. \]Obecné řešení homogenní rovnice dostaneme jako jejich lineární kombinaci:
\[v_\mathrm{h}(t)=Ae^{\mathrm{i}\Omega \mathrm{t}}+Be^{\mathrm{-i}\Omega \mathrm{t}}.\tag{4}\]Komplexní exponenciály \(e^{\mathrm{i}\Omega \mathrm{t}}\) a \(e^{\mathrm{-i}\Omega \mathrm{t}}\) přepíšeme do goniometrického tvaru:
\[e^{\mathrm{i}\Omega t}= \cos(\Omega t)+i\,\sin(\Omega t),\] \[e^{\mathrm{-i}\Omega t}= \cos(\Omega t)-i\,\sin(\Omega t)\]a dosadíme do rovnice (4):
\[v_\mathrm{h}(t)=A[\cos(\Omega t)+i\,\sin(\Omega t)]+B[\cos(\Omega t)-i\,\sin(\Omega t)].\]Po úpravě dostáváme rovnici:
\[v_\mathrm{h}(t)=(A+B)\cos(\Omega t)+i(A-B)\,\sin(\Omega t).\]Součet a rozdíl konstant A a B označíme jako nové konstanty C a D:
\[v_\mathrm{h}(t)=C\,\cos(\Omega t)+\,D\,\sin(\Omega t).\]Dostali jsme obecné řešení homogenní rovnice, kde C a D jsou reálné konstanty (protože hledáme pouze reálná řešení dané diferenciální rovnice).
b) Hledání partikulárního řešení
Partikulární řešení je jedno libovolné řešení nehomogenní diferenciální rovnice, tedy rovnice s nenulovou pravou stranou. Pro hledání tohoto řešení existují také obecné postupy, ale v jednoduchých případech bývá rychlejší vyzkoušet nějakou jednoduchou funkci, zda náhodou danou rovnici neřeší. Naše rovnice (3) má na pravé straně konstantu. Zkusme tedy za partikulární řešení nehomogenní rovnice vp dosadit konstantní funkci:
\[v_\mathrm{p}=\mathrm{konst}.\]Spočítáme derivace partikulárního řešení:
\[\dot v_\mathrm{p}=0,\] \[\ddot v_\mathrm{p}=0.\]Výrazy dosadíme do rovnice (3):
\[\ddot v_\mathrm{p}+\,\left(\frac{QB}{m}\right)^2v_\mathrm{p} =\,\left(\frac{Q}{m}\,\right)^2EB,\] \[0+\left(\frac{QB}{m}\right)^2v_\mathrm{p} =\,\left(\frac{Q}{m}\,\right)^2EB.\]Z rovnice vyjádříme vp:
\[v_\mathrm{p}B =E,\] \[v_\mathrm{p} =\frac{E}{B}.\]Konstantní funkce se ukázala jako vhodné partikulární řešení a spočítali jsme také hodnotu této konstanty.
c) Celkové řešení nehomogenní diferenciální rovnice
Obecné řešení nehomogenní diferenciální rovnice dostaneme jako součet obecného řešení homogenní rovnice a partikulárního řešení, tedy:
\[v_\mathrm{y}=v_\mathrm{h}+v_\mathrm{p},\] \[v_\mathrm{y}(t)=C\,\cos(\Omega t)+\,D\,\sin(\Omega t)+ \frac{E}{B}.\tag{5}\]d) Určení konstant C a D
Konstanty C a D určíme z počátečních podmínek. Na začátku (v čase t = 0) byla částice v klidu, tedy:
\[v_\mathrm{y}(0)=0,\] \[v_\mathrm{y}(0)=C\,\cos{0}+\,D\,\sin{0}+ \frac{E}{B}=0,\] \[C+\,\frac{E}{B}=0.\]Dostáváme velikost konstanty C:
\[C=-\frac{E}{B}.\]Pro výpočet druhé konstanty D určíme nejprve složku rychlosti vz. Pro ni platí (viz předchozí oddíl):
\[v_\mathrm{z}= \frac{m}{QB}\,\dot v_\mathrm{y}.\]Zrychlení \(\dot v_\mathrm{y}\) získáme zderivováním vztahu pro rychlost \(v_\mathrm{y}\) podle času:
\[v_\mathrm{y}(t)=C\,\cos(\Omega t)+\,D\,\sin(\Omega t)+ \frac{E}{B},\] \[\dot v_\mathrm{y}(t)=-C\Omega\,\sin(\Omega t)+D\Omega\,\cos(\Omega t).\]Složka rychlosti vz má tvar:
\[v_\mathrm{z}(t)= \frac{m\Omega}{QB}\,\left(-C\,\sin(\Omega t)+D\,\cos(\Omega t)\right).\tag{6}\]Z počátečních podmínek vz(0) = 0 určíme konstantu D:
\[v_\mathrm{z}(0)= \frac{m\Omega}{QB}\,D=0,\] \[D=0.\]Vyjádřené konstanty C a D dosadíme do obecného řešení (5):
\[v_\mathrm{y}(t)=C\,\cos{(\Omega t)}+\,D\,\sin(\Omega t)+ \frac{E}{B}=-\frac{E}{B}\,\cos(\Omega t)+ \frac{E}{B}.\]Složka rychlosti vy do směru osy y má tvar:
\[v_\mathrm{y}(t)=\frac{E}{B}(1-\,\cos(\Omega t)).\]Složku rychlosti vz vyjádříme ze vztahu (6) dosazením za konstanty C a D:
\[v_\mathrm{z}(t)= \frac{m\Omega}{QB}\,\left(-C\,\sin(\Omega t)+D\,\cos(\Omega t)\right),\] \[v_\mathrm{z}(t)= \frac{m\Omega}{QB}\,\left(\frac{E}{B}\,\sin(\Omega t)\right).\]Jestliže si uvědomíme, že jsme označili:
\[\Omega=\frac{QB}{m},\]pro složku rychlosti vz ve směry osy z dostáváme výraz:
\[v_\mathrm{z}(t)= \frac{E}{B}\,\sin(\Omega t).\]Řešení - hledání trajektorie
Vyřešením diferenciální rovnice jsme dostali vztah pro složku rychlosti vy částice ve směru osy y ve tvaru:
\[v_\mathrm{y}(t)=\frac{E}{B}(1-\,\cos(\Omega t)).\]A složku vz ve směru osy z ve tvaru:
\[v_\mathrm{z}(t)=\frac{E}{B}\,\sin(\Omega t),\]kde \(\,\Omega=\frac{QB}{m}.\)
Souřadnice polohy y a z získáme zintegrováním příslušných složek rychlosti podle času:
\[y=\int{v_\mathrm{y}}\,dt=\int{\frac{E}{B}\,\left(1-\,\cos(\Omega t)\right)}\,\mathrm{d}t,\] \[y=\frac{E}{B\Omega}\,\left(\Omega t-\sin(\Omega t)\right)+y_0.\]Pro souřadnici z získáme závislost:
\[z=\int{v_\mathrm{z}}\,\mathrm{d}t=\int{\frac{E}{B}\,\sin(\Omega t)}\,\mathrm{d}t,\] \[z=-\frac{E}{B\Omega}\,\cos(\Omega t)+z_0.\]Integrační konstanty \(y_0\) a \(z_0\) dopočítáme z počátečních podmínek. Předpokládejme, že částice je v čase \(t\,=\,0\,\mathrm{s}\) v počátku soustavy souřadnic. Potom:
\[ 0=y\left(0\right)=\frac{E}{B\Omega}\,\left(\Omega \cdot 0-\sin{\left(\Omega \cdot 0 \right)}\right)+y_0 \] \[ 0=z\left(0\right)=-\frac{E}{B\Omega}\,\cos{\left(\Omega \cdot 0\right)}+z_0 \] \[ y_0=0 \] \[ z_0=\frac{E}{B \Omega}. \]Trajektorii pohybu částice v homogenním elektromagnetickém poli popisují následující rovnice:
\[x=0,\] \[y=\frac{E}{B\Omega}\,\left(\Omega t-\sin(\Omega t)\right),\] \[z=\frac{E}{B\Omega}\left(1-\cos(\Omega t)\right),\]kde \(\Omega=\frac{QB}{m}.\)
Tvar trajektorie
Rovnice popisující trajektorii pohybu částice v homogenním elektromagnetickém poli mají tento tvar:
\[x=0,\] \[y=\frac{E}{B\Omega}\,\left(\Omega t-\sin(\Omega t)\right),\] \[z=\frac{E}{B\Omega}\left(1-\cos(\Omega t)\right),\hspace{15px}\Omega=\frac{QB}{m}.\]Jedná se o složení dvou pohybů — pohybu po kružnici v rovině yz s poloměrem \(\frac{E}{B\Omega}\) a rovnoměrného přímočarého pohybu ve směru osy y. Složením těchto dvou pohybů vznikne křivka zvaná cykloida.
V tabulkách nalezneme parametrické vyjádření prosté cykloidy ve tvaru:
\[x=0,\] \[y=a(T-\sin T),\] \[z=a(1-\cos T),\]kde a je poloměr kružnice a T velikost úhlu odvalení.
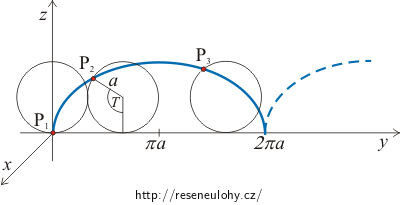
Poznámka: Pohyb částice v elektromagnetickém poli si můžeme jednoduše představit jako pohyb ventilku u jedoucího jízdního kola, kde při odvalování kola ventilek také opisuje křivku zvanou cykloida.
Odpověď
Po sepnutí homogenního elektrického pole ve směru kladné poloosy z a homogenního magnetického pole ve směru kladné poloosy x se částice bude pohybovat po křivce zvané cykloida určené rovnicemi:
\[x=0,\] \[y=\frac{E}{B\Omega}\,\left(t\Omega-\sin(\Omega t)\right),\] \[z=\frac{E}{B\Omega}\left(1-\cos(\Omega t)\right),\,\,\,\,\,\,\,\,\,\,\,\Omega=\frac{QB}{m}.\]Dynamický prvek
V následujícím apletu je zobrazena trajektorie nabité částice v magnetickém a elektrickém poli. Pomocí posuvníků lze nastavit velikost magnetické indukce a velikost elektrické intenzity. Aplet lze spustit jako animaci, nebo je možné ovládat pohyb částice pomocí prvního posuvníku.
Úkoly pro práci s apletem
- Spusťte animaci a pozorujte vykreslování trajektorie. O jakou se jedná křivku?
- Prozkoumejte a zjistěte, jakým způsobem je závislý tvar trajektorie na magnetické indukci a elektrické intenzitě. (Nastavujte různé hodnoty pomocí posuvníků.)
- Nastavte \(B=1\space\mathrm{T}\) a \(E=1\space\frac{\mathrm{N}}{\mathrm{C}}\) a nechte vykreslit trajektorii. Nyní změňte oba parametry tak, aby se nově vykreslená trajektorie překrývala s původní.



