Poloha těžiště komolého kužele
Úloha číslo: 1025
Je dán homogenní komolý kužel o výšce h, poloměru dolní podstavy r1 a poloměru horní podstavy r2 (r1 > r2).
Spočtěte polohu jeho těžiště.
Nápověda 1
Nejdřív by bylo vhodné si celou situaci nakreslit. Umístěte vhodně komolý kužel do kartézské soustavy souřadnic a v obrázku vyznačte parametry tělesa.
Rozmyslete si, jaký vztah použijete pro výpočet těžiště (vzorec z mechaniky).
Pak si rozmyslete, jaké souřadnice bude těžiště mít. Při úvaze využijte symetrii komolého kužele (některé souřadnice budou nulové apod.).
Nápověda 2
Ve vzorci pro výpočet těžiště se nacházejí dva objemové integrály. Integrál v čitateli lze však převést na jednorozměrný integrál, uvědomíte-li si, že těžiště má nenulovou jenom jednu souřadnici (viz výše).
Zkuste si rozmyslet, jak by bylo vhodné komolý kužel „rozsekat“, a vyjádřete elementární objem dV jednotlivých elementárních útvarů.
Nápověda 3
Ve vztahu pro elementární objem dV se vyskytuje druhá mocnina poloměru r, jehož vyjádření zatím neznáme. Poloměr válečků r se mění v závislosti na souřadnici y.
Vyjádřete poloměr r pomocí zadaných parametrů tělesa. V obrázku níže je zakreslena výška „čárkovaného“ kužele v, kterou využijete při výpočtu. Zkuste využít podobnost pravoúhlých trojúhelníků na obrázku.
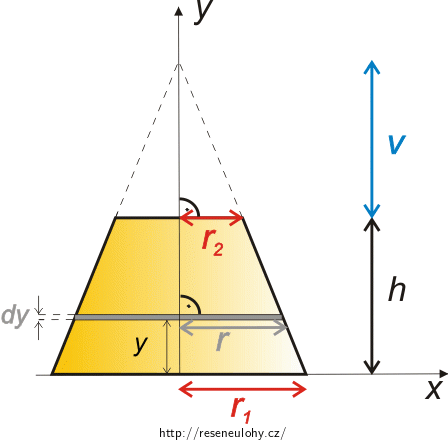
Nápověda 4
Ve vztahu pro element dV
\[ \mathrm{d}V = \pi r^2 \mathrm{d}y = \pi \frac{r_{\mathrm{2}}^2}{v^2}(h + v - y)^2 \mathrm{d}y \]se vyskytuje ještě jedna neznámá, a to výška v.
Zkuste ji vyjádřit pomocí známých parametrů tělesa, pomozte si při tom obrázkem níže. Využijte podobnost pravoúhlých trojúhelníků vyznačených na obrázku.
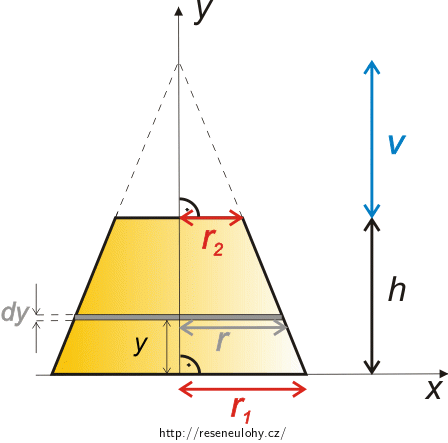
Nápověda 5
Nyní už nezbývá nic jiného než dosadit dílčí výsledky do vztahu pro těžiště komolého kužele. Nezapomeňte, že stačí spočítat jenom souřadnici yT, protože díky symetrii jsou souřadnice xT a zT nulové.
Po dosazení si rozmyslete meze integrace.
Celkové řešení
Komolý kužel (pohled zepředu) jsme umístili do kartézské soustavy souřadnic (viz obrázek níže).
Poznámka: Osa z je kolmá na osy x, y a míří směrem k nám z nákresny.
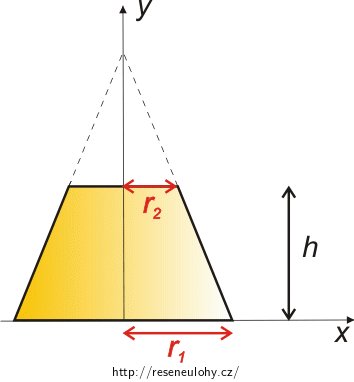
Využijeme známý vzorec z mechaniky pro výpočet polohy těžiště:
\[ \vec{r_{\mathrm{T}}} = \frac{\int_{V}\rho \vec{r} \mathrm{d}V}{\int_{V}\rho \mathrm{d}V} \hspace{3px}. \]Komolý kužel je symetrický vůči ose y, proto bude mít jeho těžiště nenulovou jenom souřadnici y.
Komolý kužel „rozsekáme“ na „válečky“ o poloměru r a elementární výšce dy, jak je možné vidět na obrázku níže.
Poznámka: Slovo válečky je uvedeno v uvozovkách proto, že se jedná vlastně o komolé kužele o elementární výšce. Dále v textu uvozovky vynecháváme.
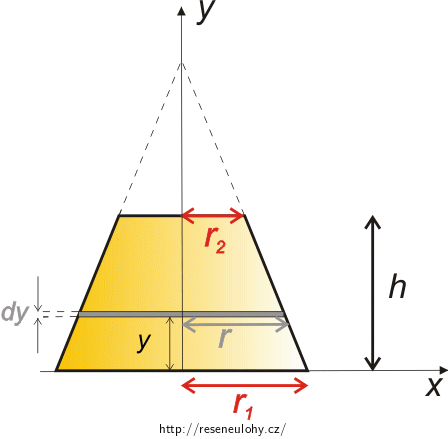
Je zřejmé, že poloměr válečků r se bude měnit v závislosti na souřadnici y.
Nyní je potřeba vyjádřit elementární objem válečků dV:
\[ \mathrm{d}V = S \mathrm{d}y = \pi r^2 \mathrm{d}y . \]Ve vztahu pro elementární objem dV se vyskytuje druhá mocnina poloměru r, jehož vyjádření zatím neznáme. Poloměr válečků r se mění v závislosti na souřadnici y. V obrázku níže je zakreslena výška „čárkovaného“ kužele v, kterou využijeme při výpočtu.

Z podobnosti pravoúhlých trojúhelníků vyplývá
\[ \frac{r}{h + v - y} = \frac{r_{\mathrm{2}}}{v} \] \[ r = \frac{r_{\mathrm{2}}}{v}(h + v - y) . \]Po umocnění obou stran rovnice získáváme vyjádření r2, které následně dosadíme do vztahu pro elementární objem dV
\[ r^2 = \frac{r_{\mathrm{2}}^2}{v^2}(h + v - y)^2 \] \[ \mathrm{d}V = \pi r^2 \mathrm{d}y = \pi \frac{r_{\mathrm{2}}^2}{v^2}(h + v - y)^2 \mathrm{d}y . \]Ve vztahu pro element dV se vyskytuje ještě jedna neznámá, a to výška v.
Vyjádříme jí pomocí známých parametrů tělesa. Využijeme podobnost pravoúhlých trojúhelníků vyznačených na obrázku níže.

Z podobnosti pravoúhlých trojúhelníků znázorněných na obrázku výše dostáváme
\[ \frac{r_{\mathrm{1}}}{h + v} = \frac{r_{\mathrm{2}}}{v} \] \[ {r_{\mathrm{1}}}v = r_{\mathrm{2}} (h + v) \] \[ {r_{\mathrm{1}}}v = r_{\mathrm{2}} h + r_{\mathrm{2}} v \] \[ v (r_{\mathrm{1}} - r_{\mathrm{2}}) = r_{\mathrm{2}} h \] \[ v = \frac{r_{\mathrm{2}} h}{r_{\mathrm{1}} - r_{\mathrm{2}}}. \]Za v dosadíme až po integrování, protože to bude formálně jednodušší.
Nyní už nezbývá nic jiného než dosadit dílčí výsledky do vztahu pro těžiště komolého kužele.
Pro polohu těžiště platí:
\[ \vec{r_{\mathrm{T}}} = \frac{\int_{V}\rho \vec{r} \mathrm{d}V}{\int_{V}\rho \mathrm{d}V} \hspace{3px}. \]Po uvážení, že nenulová je jenom souřadnice yT, dostáváme
\[ y_{\mathrm{T}} = \frac{\int_0^h \rho y \pi r^2 \mathrm{d}y} {\int_V \rho \mathrm{d}V}. \]Pro jednoduchost spočteme nejdřív integrál v čitateli
\[ \int_0^h \rho y \pi r^2 \mathrm{d}y = \int_0^h \rho y \pi \frac{r_{\mathrm{2}}^2}{v^2}(h + v - y)^2 \mathrm{d}y , \]využijeme linearitu integrálu (tj. konstanty lze dát před integrál).
Poznámka: Hustotu ρ lze taky vytknout před integrál, protože je díky homogenitě komolého kužele konstantní.
\[ \int_0^h \rho y \pi \frac{r_{\mathrm{2}}^2}{v^2}(h + v - y)^2 \mathrm{d}y = \rho \pi \frac{r_{\mathrm{2}}^2}{v^2}\int_0^h y (h + v - y)^2 \mathrm{d}y = \] \[ = \rho \pi \frac{r_{\mathrm{2}}^2}{v^2}\int_0^h y \bigg[(h + v)^2 - 2(h + v)y + y^{2}\bigg]\mathrm{d}y = \rho \pi \frac{r_2^2}{v^2}\int_0^h \bigg[ y(h + v)^2 - 2(h + v)y^{2} + y^{3}\bigg]\mathrm{d}y = \] \[ = \rho \pi \frac{r_2^2}{v^2} \left[ (h + v)^2 \frac{y^2}{2} - 2(h + v)\frac{y^{3}}{3} + \frac{y^{4}}{4} \right]_0^h = \rho \pi \frac{r_2^2}{v^2} \bigg[ (h + v)^2 \frac{h^2}{2} - 2(h + v)\frac{h^{3}}{3} + \frac{h^{4}}{4} \bigg] = \] \[ = \rho \pi \frac{r_2^2}{v^2} \bigg( \frac{h^4}{2} + h^3v + \frac{v^2h^2}{2} - \frac{2}{3}h^4 - \frac{2}{3}vh^3 +\frac{h^4}{4} \bigg) = \] \[ = \rho \pi \frac{r_2^2}{v^2} \bigg( \frac{h^4}{12} +\frac{1}{3}vh^3 + \frac{1}{2}v^2h^2 \bigg) = \rho \pi \frac{r_2^2}{v^2}\frac{h^2}{12} \bigg( h^2 + 4vh + 6v^2\bigg) . \]Po dosazení \[ v = \frac{r_2 h}{r_1 - r_2} \] dostáváme
\[ \rho \pi \frac{r_2^2h^2(r_1 - r_2)^2}{12r_2^2h^2 }\bigg[ h^2 + 4\frac{r_2h^2}{r_1 - r_2} + 6\frac{r_2^2h^2}{(r_1 - r_2)^2}\bigg] = \rho \pi \frac{(r_1 - r_2)^2}{12} \bigg[\frac{h^2(r_1 - r_2)^2 + 4r_2h^2(r_1 - r_2) + 6r_2^2h^2 }{(r_1 - r_2)^2} \bigg] =\] \[ =\frac{1}{12}\rho \pi h^2 (r_1^2 - 2r_1r_2 + r_2^2 +4r_1r_2 - 4r_2^2 + 6r_2^2) = \frac{1}{12}\rho \pi h^2 (r_1^2 + 2r_1r_2 + 3r_2^2 ). \]Pro integrál ve jmenovateli ve vzorci pro výpočet těžiště platí
\[\int_V \rho \mathrm{d}V = \rho \int_V \mathrm{d}V = \rho \pi \frac{r_2^2}{v^2}\int_0^h (h + v - y)^2 \mathrm{d}y . \]Analogickým výpočtem jako předtím bychom dostali až na hustotu ρ vzorec pro výpočet objemu komolého kužele, který je známý již ze střední školy
\[ V = \int_V \mathrm{d}V = \frac{1}{3}\pi h \left(r_1^2 + r_1r_2 + r_2^2\right). \]Pro souřadnici yT těžiště tedy platí
\[ y_{\mathrm{T}} = \frac{\frac{1}{12}\rho \pi h^2 \left(r_1^2 + 2r_1r_2 + 3r_2^2 \right)}{ \frac{1}{3}\rho \pi h \left(r_1^2 + r_1r_2 + r_2^2\right)} \]Po zkrácení dostáváme vztah pro hledanou souřadnici
\[y_{\mathrm{T}} = \frac{h}{4}\frac{\left(r_1^2 + 2r_1r_2 + 3r_2^2 \right)}{\left(r_1^2 + r_1r_2 + r_2^2\right)}. \]Odpověď
Těžiště homogenního komolého kužele leží na ose jeho symetrie ve výšce
\[y_{\mathrm{T}} = \frac{h}{4}\frac{\left(r_1^2 + 2r_1r_2 + 3r_2^2 \right)}{\left(r_1^2 + r_1r_2 + r_2^2\right)} . \]

