Těžiště jednoho oblouku asteroidy
Úloha číslo: 2305
Je dána homogenní asteroida o délce ramene a, jejíž střed je umístěn v počátku kartézského souřadného systému, vrcholy ramen jsou umístěny na souřadných osách x a y. Určete souřadnice těžiště jednoho oblouku asteroidy umístěného v prvním kvadrantu (v obrázku tučně červeně).
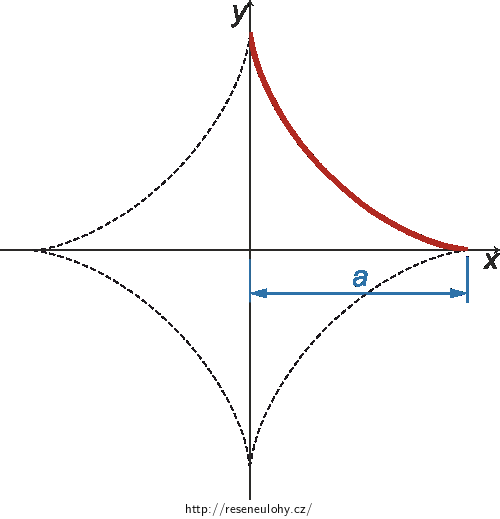
Rozbor
Budeme vycházet ze vztahu pro polohu těžiště obecného tuhého tělesa, který rozdělíme na x-ovou a y-ovou složku. Tento vztah obsahuje dva integrály, kdy jeden dokážeme vyřešit jednoduchou úvahou, druhý, složitější, postupnými úpravami. V obou případech se integruje podle hmotnosti. U složitějšího nejprve využijeme známý vztah mezi délkou, délkovou hustotou a hmotností, poté využijeme vztah pro délku elementu obecné křivky a na závěr dosadíme za souřadnice výrazy z parametrických rovnic. Výsledkem bude integrál, který dokážeme po běžných algebraických úpravách integrovat s použitím metody substituce. Ve výsledku integrace jen nahradíme neznámé veličiny a získáme souřadnice těžiště v závislosti na délce ramene a.
Nápověda
K vyřešení této úlohy je zapotřebí znát vzorec pro polohu těžiště obecného tuhého tělesa, vztah mezi délkovou hustotou, délkou a hmotností, vztah pro délku elementu obecné křivky (případně délku obecné křivky), parametrické rovnice asteroidy, dokázat je derivovat, znát význam jejich parametru a znát délku asteroidy v závislosti na délce ramene a. Pokud máte s jakoukoliv z uvedených oblastí problémy, doporučujeme nejprve projít úlohy Délka asteroidy, Délka oblouku cykloidy, Těžiště cykloidy, ve kterých jsou všechny zmíněné vztahy podrobně odvozeny.
Řešení
Mohli bychom spočíst každou souřadnici zvlášť, je však možné si ušetřit práci, pokud si uvědomíme, že původní asteroida je křivka symetrická podle přímky y = x a je tedy podle ní symetrický i náš oblouk. Z toho plyne, že obě souřadnice jeho těžiště budou shodné. Budeme vycházet z obecného vztahu pro polohu těžiště \(\vec r_t\)
\[\vec r_t=\frac{\int_\Gamma \vec r \mathrm d m}{\int_\Gamma \mathrm d m},\]kde \(\vec r\) je poloha jednoho elementu hmotnosti dm, \(\Gamma\) značí, že integrujeme po celé křivce, tedy po oblouku asteroidy a dm značí, že integrujeme podle hmotnosti (neboli integrací sčítáme infinitezimální elementy hmotnosti).
Tento vztah je odvozen v úloze Těžiště cykloidy, v části Nápověda a, Řešení nápovědy a.
Budeme počítat y-ovou složku (x-ová by se počítala naprosto analogicky). Z výchozího vztahu tedy využijeme jen y-ovou složku
\[y_t=\frac{\int_\Gamma y \ \mathrm d m}{\int_\Gamma \mathrm d m}.\]Integrál ve jmenovateli dá celkovou hmotnost oblouku asteroidy, neboť jde o součet elementů hmotnosti přes celý oblouk, tedy
\[y_t=\frac{1}{m} \int_\Gamma y \ \mathrm d m.\]V dalším kroku nahradíme integrování podle hmotnosti integrací podle délky pomocí vztahu pro délkovou hmotnostní hustotu \(\lambda\)
\[\lambda=\frac{\mathrm dm}{\mathrm ds},\]který dosadíme do vztahu pro \(y_t\):
\[y_t=\frac{1}{m} \int_\Gamma y \ \lambda \ \mathrm d s.\]Dále integraci podle délky nahradíme integrací podle parametru užitím vztahu pro délku elementu obecné křiky ds
\[ \mathrm{d} s= \sqrt{\left( \frac{\mathrm{d} x}{\mathrm{d} t} \right)^2+ \left( \frac{\mathrm{d} y}{\mathrm{d} t} \right)^2} \mathrm{d} t\](byl odvozen v úloze Délka oblouku cykloidy v Nápověda, Řešení nápovědy).
Tím získáme
\[ y_t= \frac{1}{m} \int_\Gamma y \ \lambda \ \sqrt{\left( \frac{\mathrm{d} x}{\mathrm{d} t} \right)^2+ \left( \frac{\mathrm{d} y}{\mathrm{d} t} \right)^2} \mathrm{d} t.\]Do tohoto vztahu dosadíme za souřadnice x, y parametrické rovnice asteroidy
\[x=a \ \cos^3 t\] \[y=a \ \sin^3 t.\]Zároveň si určíme i derivace parametrických rovnic, podle parametru t
\[\frac{\mathrm dx}{\mathrm dt}=-3a \ \cos^2 t \ \sin t\] \[\frac{\mathrm dy}{\mathrm dt}=3a \ \sin^2 t \ \cos t.\]Dosazením parametrických rovnic a jejich derivací získáme vztah
\[y_t=\frac{1}{m} \int_\Gamma a \ \lambda \ \sin^3 t \sqrt{(-3a \ \cos^2 t \ \sin t)^2 + (3a \ \sin^2 t \ \cos t)^2} \mathrm dt.\]V tomto vztahu nejprve určíme integrační meze.
Integrujeme podle parametru t. Pro celou asteroidu v parametrickém vyjádření platí, že parametr t může nabývat hodnot z intervalu \((0;2\pi\rangle\), my však potřebujeme pouze první čtvrtinu asteroidy, parametr proto zúžíme na \((0;\frac{\pi}{2}\rangle\) a právě krajní body tohoto intervalu nyní použijeme jako integrační meze
\[y_t=\frac{1}{m} \int_0^\frac{\pi}{2} a \ \lambda \ \sin^3 t \sqrt{(-3a \ \cos^2 t \ \sin t)^2 + (3a \ \sin^2 t \ \cos t)^2} \mathrm dt.\]Tento vztah budeme dále postupně upravovat. V prvním kroku umocníme výrazy v závorkách
\[y_t=\frac{1}{m} \int_0^\frac{\pi}{2} a \ \lambda \ \sin^3 t \ \sqrt{9a^2 \ \cos^4 t \ \sin^2 t + 9a^2 \ \sin^4t \ \cos^2t}\ \mathrm dt.\]Vytkneme vše, co mají sčítance pod odmocninou společné
\[y_t=\frac{1}{m} \int_0^\frac{\pi}{2} a \ \lambda \ \sin^3 t \ \sqrt{9a^2 \ \cos^2t \ \sin^2t \ (\sin^2t+\cos^2t)}\ \mathrm dt.\]V závorce jsme tím dostali „goniometrickou jedničku“, tedy výraz v závorce je rovný jedné. Vše zbylé pod odmocninou je v druhé mocnině, tedy snadno provedeme odmocnění
\[y_t=\frac{1}{m} \int_0^\frac{\pi}{2} a \ \lambda \ \sin^3 t \ 3a \ \cos t \ \sin t \ \mathrm dt.\]Vytkneme před integrál vše, co nezávisí na t
\[y_t=3\frac{a^2 \lambda}{m} \ \int_0^\frac{\pi}{2} \sin^4 t \ \cos t \mathrm \ dt.\]V tomto tvaru již dokážeme integrovat za použití substituční metody. Substituci zvolíme
\[u=\sin t\] \[\mathrm du=\cos t \ \mathrm dt.\]Substituční meze přepočteme dosazením původních mezí do prvního řádku substituce. Po dosazení substituce získáme
\[y_t=3 \frac{a^2 \lambda}{m} \int_0^1 u^4 \mathrm du.\]Provedeme integraci
\[y_t=3 \frac{a^2 \lambda}{m} \left[ \frac{u^5}{5} \right] _0^1 = \frac{3}{5} \frac{a^2 \lambda}{m}.\]Délková hmotnostní hustota \(\lambda\) nebyla zadána, nahradíme ji proto ze vztahu
\[\lambda=\frac{m}{s},\]kde s je délka křivky, m její celková hmotnost. Dosazením dostaneme
\[y_t=\frac{3}{5} \frac{a^2}{s}.\]Jako poslední úpravu dosadíme délku oblouku asteroidy s. V úloze Délka asteroidy byla spočtena délka celé asteroidy \(s_c=6a\). Délka jednoho oblouku tedy je \(s=\frac{6}{4}a=\frac{3}{2}a\). Po dosazení dostáváme výsledek
\[y_t=\frac{2}{5}a.\]x-ová souřadnice je kvůli symetrii asteroidy stejná, tedy souřadnice těžiště jednoho oblouku asteroidy jsou
\[\vec r_t= \left[ \frac{2}{5}a; \frac{2}{5}a \right].\]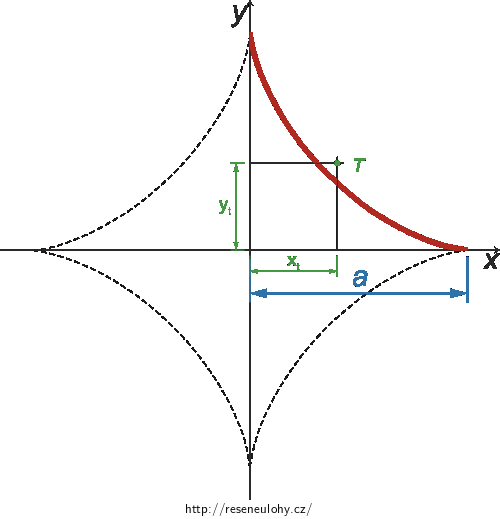
Odpověď
Souřadnice těžiště jednoho oblouku asteroidy jsou
\[\vec r_t= \left[ \frac{2}{5}a; \frac{2}{5}a \right].\]

